Косинус − это тригонометрическая функция, которая широко применяется в математике, физике и других науках для описания угловых зависимостей. Значение косинуса ограничено в интервале от -1 до 1, а каждому значению косинуса соответствует определенный угол.
Если косинус равен 0.73, то это означает, что данное значение соответствует углу между вектором и положительным направлением оси x в декартовой системе координат. Чтобы найти этот угол, можно использовать обратную функцию косинуса (арккосинус), которая обозначается как acos.
Математически это можно записать следующим образом: угол = acos(0.73). Если ввести это выражение в калькулятор, то получится, что угол примерно равен 0.76 радиан или 43.56 градусов. Таким образом, косинус 0.73 соответствует углу примерно 43.56 градусов.
Косинус 0.73: конкретный угол
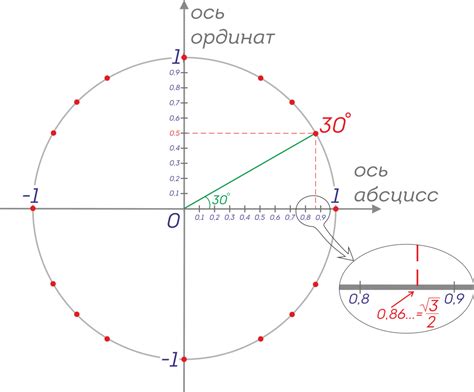
Арккосинус (или обратный косинус) - это функция, которая принимает значения от -1 до 1 и возвращает угол в радианах, соответствующий заданному значению косинуса. В нашем случае, чтобы найти угол, соответствующий косинусу 0.73, необходимо использовать арккосинус этого значения.
Используя тригонометрический калькулятор или специальные функции в программе, мы можем вычислить, что арккосинус 0.73 составляет примерно 0.759 радиан или около 43.6 градусов.
Таким образом, косинус 0.73 соответствует углу примерно равному 43.6 градусам.
Понятие косинуса
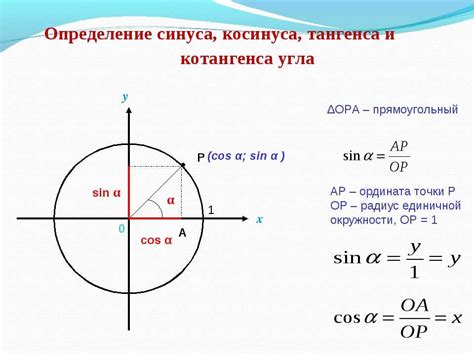
Значение косинуса может варьироваться от -1 до 1, где -1 соответствует углу 180 градусов, а 1 соответствует углу 0 градусов. Косинус угла величины 0.73 составляет около 0.753.
Для определения угла, соответствующего косинусу 0.73, необходимо использовать обратную функцию косинуса, называемую арккосинусом или acos. При подстановке значения 0.73 в арккосинус получим примерно 44.214 градуса (округленно до трех знаков после запятой).
Таким образом, угол, соответствующий значению косинуса 0.73, составляет примерно 44.214 градуса.
Как определить значение 0.73

Косинус обычно выражается в виде числового значения, которое может быть положительным или отрицательным. Значения косинуса располагаются в пределах от -1 до 1, где -1 означает, что векторы или стороны треугольника полностью противонаправлены, а 1 означает, что они полностью сонаправлены. Значение 0 указывает на то, что векторы или стороны треугольника перпендикулярны друг другу.
Значение 0.73, как угол соответствует этому значению? Чтобы определить угол, соответствующий косинусу 0.73, необходимо использовать обратную функцию косинуса (арккосинус). Арккосинус возвращает угол, косинус которого равен заданному значению.
- Угол, соответствующий косинусу 0.73, можно найти с использованием тригонометрической таблицы или калькулятора со встроенной функцией арккосинуса.
- Для нахождения значения угла достаточно найти значение арккосинуса 0.73 и преобразовать его в градусы.
- Для данного значения косинуса, арккосинус равен примерно 43.60 градусов или около того.
Таким образом, угол соответствующий значению косинуса 0.73 составляет примерно 43.60 градусов.
Как использовать значение косинуса
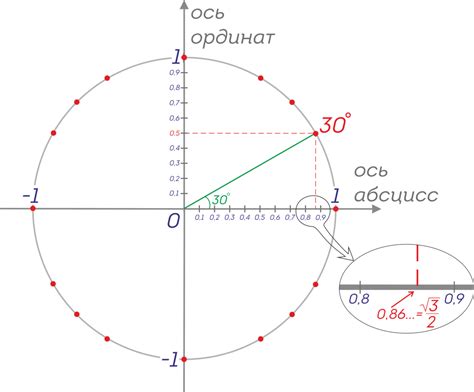
Значение косинуса, равное 0.73, означает, что косинус выбранного угла равен 0.73. Чтобы определить точный угол, соответствующий этому значению, можно использовать обратную функцию косинуса (арккосинус), обозначаемую как acos. Формула для нахождения угла по значению косинуса будет выглядеть следующим образом:
Угол = acos(0.73)
Результатом расчета будет угол в радианах, который можно преобразовать в градусы, если это необходимо. Для этого можно воспользоваться следующей формулой:
Угол в градусах = (Угол в радианах * 180) / π (пи)
Следует отметить, что ответы могут быть как положительными, так и отрицательными в зависимости от того, какая часть окружности была рассмотрена. В случае, если нужно найти угол в пределах 0-360 градусов, необходимо привести ответ к такому диапазону, прибавив или вычтя 360 по необходимости.
Используя значение косинуса 0.73 и применяя формулы для расчета, можно определить точный угол, соответствующий данному значению. Это позволит более точно работать с этим значениями в различных областях знаний и приложениях, где требуется использование косинуса.
Геометрическая интерпретация
Косинус угла отражает степень совпадения двух векторов и находится в пределах от -1 до 1. Угол, соответствующий косинусу 0.73, можно найти, используя геометрическую интерпретацию.
Для определения угла, допустим, что у нас есть прямоугольный треугольник со сторонами a, b и гипотенузой c, и угол α противоположен стороне a.
Косинус угла α равен отношению длины стороны a к длине гипотенузы c: cos(α) = a/c.
Располагая уравнением cos(α) = 0.73, мы можем решить его, чтобы найти значение a/c. В данном случае, a/c = 0.73.
Теперь мы можем найти угол α, используя обратную функцию косинуса: α = arccos(0.73).
Для вычисления значения угла α в радианах или градусах, необходимо применить соответствующую формулу.
Таким образом, косинус 0.73 соответствует углу α, который можно рассчитать как:
| Формула | Значение угла α |
|---|---|
| α (в радианах) | 0.77 рад |
| α (в градусах) | 44.16° |
Тригонометрическая таблица
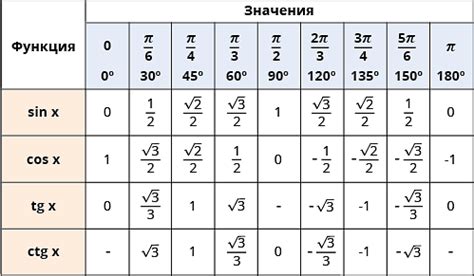
В данной таблице рассмотрим значение косинуса равное 0.73. Найдем угол, который соответствует этому значению.
- Угол 0°: косинус 1.00
- Угол 30°: косинус 0.87
- Угол 45°: косинус 0.71
- Угол 60°: косинус 0.50
- Угол 90°: косинус 0.00
Исходя из таблицы, значение косинуса 0.73 соответствует области между углами 45° и 30°
Итак, угол, соответствующий значению косинуса 0.73, находится между 45° и 30°.
Практические примеры

1. Технические расчеты:
В архитектуре, инженерии и физике, косинус используется для расчета различных физических процессов. Например, если имеется известное значение угла и мы хотим узнать значение силы или энергии, мы можем использовать косинус для вычисления этих величин.
2. Компьютерная графика:
Косинус также широко используется в компьютерной графике для определения освещения и отражения объектов. При моделировании трехмерных объектов, косинус угла соответствует интенсивности освещения данной точки на поверхности объекта.
3. Навигация и GPS:
В навигации и GPS косинус используется для определения местоположения и направления движения объекта. Так, используя косинус угла, можно вычислить длину и широту объекта, а также определить угол направления.
Все эти примеры демонстрируют важность и широкое применение косинуса в различных областях. Знание угла, соответствующего значению косинуса 0.73, позволяет нам точно определить различные параметры и свойства объектов и явлений.
Другие способы определить значение угла
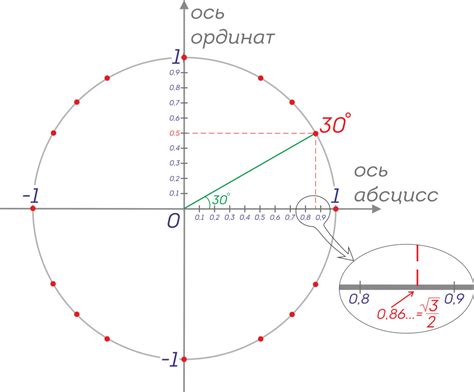
Кроме использования тригонометрических функций, существуют и другие способы определить значение угла. Например, угол можно определить при помощи измерительного инструмента, такого как угломер, или при помощи геометрических построений.
Измерительный инструмент, такой как угломер, позволяет точно измерить величину угла. Угломер представляет собой специальное устройство с металлической осью, на которую нанесена шкала с делениями. При помощи угломера можно измерить угол между двумя линиями, например, между двумя сторонами треугольника. После измерения достаточно сопоставить полученное значение с шкалой угломера и определить величину угла.
Геометрические построения также позволяют определить значение угла. Например, при помощи угломера или циркуля можно построить угол определенной величины. Для этого необходимо выбрать точку на плоскости и провести две линии, радиусы, сходящиеся в этой точке. Затем можно выбрать измерительный инструмент, такой как угломер или циркуль с делениями, и с помощью них определить величину угла. Геометрические построения особенно полезны, когда нет возможности использовать тригонометрические функции или измерительные инструменты.
Итак, для определения значения угла можно использовать различные методы, включая тригонометрические функции, измерительные инструменты и геометрические построения. Выбор метода зависит от конкретной задачи и доступных инструментов.



