Дивергенция и конвергенция - термины из математического анализа, которые используются для описания поведения последовательностей или функций в точке или на бесконечности.
Дивергенция определяется как изменение функции или последовательности, когда ее значения отдаляются друг от друга. Если последовательность или функция имеют дивергенцию, значит они расходятся, и их значения все больше и больше отдаляются друг от друга.
Конвергенция, наоборот, описывает поведение последовательности или функции, когда ее значения приближаются друг к другу. Если последовательность или функция сходятся, значит ее значения становятся все ближе и ближе к какой-то предельной точке или конечному значению.
Примером дивергенции может служить последовательность натуральных чисел: 1, 2, 3, 4, ... В этом случае значения последовательности растут бесконечно и между ними нет предельной точки.
Примером конвергенции может служить последовательность десятичных дробей: 0.9, 0.99, 0.999, 0.9999, ... В этом случае значения последовательности приближаются к предельному значению 1, и между ними нет большого расстояния.
Что такое дивергенция и конвергенция
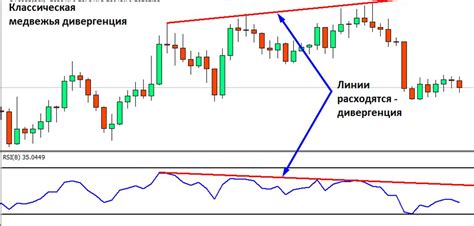
Дивергенция указывает на то, насколько быстро или медленно функция или вектор расходятся относительно точки или области. Если дивергенция положительна, значит функция или вектор "расходятся", то есть их значения увеличиваются или уменьшаются с ростом расстояния от точки или в области. Если дивергенция отрицательна, то функция или вектор "сходятся", то есть их значения уменьшаются или увеличиваются с ростом расстояния от точки или в области. Если дивергенция равна нулю, то функция или вектор "константны", то есть их значения не меняются с расстоянием от точки или в области.
Конвергенция, с другой стороны, указывает на то, насколько функция или вектор приближаются к определенной точке или области. Если функция или вектор сходятся, значит их значения приближаются к некоторому значению с увеличением расстояния от точки или в области. Если функция или вектор расходятся, то их значения становятся все больше и больше с увеличением расстояния от точки или в области.
На практике, дивергенция и конвергенция используются для описания поведения физических полей, таких как электрическое, магнитное или гравитационное поле. Они также применяются в численных методах для решения дифференциальных уравнений и в других областях науки и инженерии.
Определение понятий

Конвергенция - это противоположное понятие дивергенции. Конвергенция описывает сходимость или сближение двух точек или векторов друг с другом. Векторная конвергенция обозначает, насколько поле векторов сходится к данной точке. Если конвергенция равна нулю, это означает, что поле является равномерным или нерасходящимся. Если конвергенция не равна нулю, это говорит о том, что поле сходится или сближается с данной точкой.
Дивергенция и конвергенция - это важные понятия в математике и физике, которые помогают описывать изменения величин и направлений в пространстве. Они применяются в различных областях, таких как векторное поле, электромагнетизм, гидродинамика, оптика и других науках. Знание этих понятий позволяет лучше понимать происходящие процессы и предсказывать их дальнейшее развитие.
Дивергенция в физике

Векторное поле можно представить как набор векторов, расположенных в каждой точке пространства. Дивергенция векторного поля определяется с помощью понятия частной производной, и показывает, насколько интенсивно векторы поля сходятся или уходят друг от друга в каждой точке пространства.
Дивергенция обозначается обычно символом ∇·F, где ∇ («набла») - оператор, а F - векторное поле. Если дивергенция векторного поля равна нулю, то можно сказать, что в данной точке нет источников или стоков этого поля.
Дивергенция играет важную роль в физике, особенно в уравнениях, описывающих законы сохранения. Она позволяет выразить закон сохранения массы, импульса, энергии и других величин в виде дифференциальных уравнений.
Примерами использования дивергенции в физике являются уравнения Максвелла, описывающие электромагнитное поле, уравнение неразрывности в гидродинамике, а также законы сохранения энергии и импульса.
Примеры дивергенции в природе

1. Морские течения: Морские течения могут быть примером дивергенции. Когда горячая вода в океане движется от экватора к полюсам, она начинает охлаждаться. В результате часть тепла передается в атмосферу, и эти движения морской воды создаются вверху полюсов воздуховоды, которые движутся в противоположных направлениях.
2. Распространение растений и животных: Эволюция привела к появлению различных видов растений и животных на планете Земля. Каждый вид развивается в свою сторону и адаптируется к своей среде обитания. В результате возникает дивергенция в особенностях строения и поведения живых существ, что позволяет им разнообразно используют доступные ресурсы для выживания.
3. Скопления звезд: В галактиках, таких как Млечный Путь, происходит дивергенция звезд. Миллионы звезд расходятся от центральной точки и движутся во все стороны. Это создает красивые и сложные структуры, такие как спиральные или сферические скопления.
4. Разветвление реки: Потоки воды в реке также могут претерпевать дивергенцию. Когда река встречает преграду, такую как горы или скалы, потоки воды начинают разделяться и двигаться в разные направления. Это создает новые русла, притоки и изменяет ландшафт.
Все эти примеры демонстрируют концепцию дивергенции в разных аспектах природы. Они помогают нам лучше понять, как разнообразие и изменение могут возникать из единого источника. Эти явления являются очень интересными и важными для изучения и понимания нашего мира.
Конвергенция и ее иллюстрация
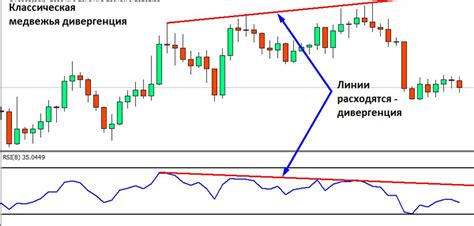
Примером конвергенции может служить развитие моды и стилей в искусстве. В основе этого процесса лежит сближение и комбинирование различных элементов идеи, характерных для разных периодов искусства. При этом возникает новое творческое решение, обогащенное вариациями и инновационными идеями.
Применение дивергенции и конвергенции в науке
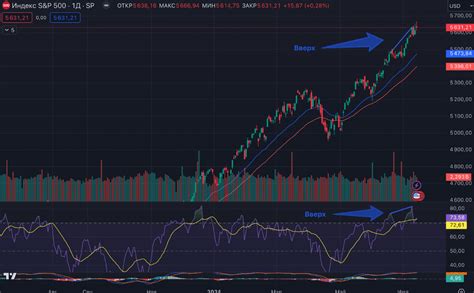
В физике, дивергенция используется для описания распределения потока векторного поля. Она позволяет определить, с какой силой масса или энергия источника распространяется или расходится из определенной точки или области. Например, дивергенция газового потока может быть использована для описания скорости расхода газа из определенного объема или разность концентраций в разных точках пространства.
Конвергенция, с другой стороны, используется для описания схожих точек или объектов, которые сходятся в одной области или точке. Например, в математике, ряд, который сходится к определенному числу, может быть описан с помощью конвергенции. Также конвергенция может использоваться для анализа сходимости алгоритмов в численных методах и компьютерных моделях.
В области искусственного интеллекта и машинного обучения, дивергенция и конвергенция используются для определения сходимости моделей. Например, в алгоритмах кластеризации, определение конвергенции может указать на то, что модель достигла оптимального разбиения данных на кластеры. Дивергенция, с другой стороны, может использоваться для оценки различий между двумя разными моделями или распределениями данных.
В целом, дивергенция и конвергенция играют важную роль в науке, обеспечивая качественное описание и анализ различных процессов и явлений. Они позволяют исследователям более точно определить и понять свойства и характеристики различных систем и моделей, а также применять их в различных практических областях знаний.



