Комплексные числа - это числа, состоящие из двух частей: действительной и мнимой. Действительная часть представляет собой обычное вещественное число, а мнимая часть имеет вид произведения на мнимую единицу i, где i - корень из -1. Такое представление чисел позволяет решать математические задачи, которые невозможно решить с помощью обычных вещественных чисел.
Основное значение комплексных чисел заключается в том, что они позволяют нам работать с математическими объектами, которые не имеют аналогов среди вещественных чисел. Например, комплексные числа используются в физике для описания электрических цепей, в финансах для моделирования стоимости финансовых инструментов, а также в теории вероятности и статистике.
Кроме того, комплексные числа широко применяются в математике для решения уравнений, включая квадратные и кубические уравнения. В радиотехнике комплексные числа используются для анализа и проектирования электрических схем и систем связи. Они также находят применение в физике при описании колебательных процессов и волновых явлений, таких как световые волны и звуковые волны.
Значение комплексных чисел в математике

Одно из важных применений комплексных чисел - решение уравнений, которые не имеют действительных корней. Например, уравнение x^2 + 1 = 0 не имеет действительных корней, но его можно решить с помощью комплексных чисел. Решение данного уравнения будет x = ±i, где i - мнимая единица.
Комплексные числа широко используются в электротехнике и физике. Они позволяют описывать колебания и взаимодействие различных физических величин. Например, комплексное сопротивление используется для описания электрических цепей, а комплексные амплитуды используются для описания колебаний волн в физике.
Комплексные числа также играют важную роль в теории функций, где они используются для анализа и описания поведения функций в комплексной плоскости. Они помогают решать различные интегральные и дифференциальные уравнения, а также находить точки минимума и максимума функций.
Использование комплексных чисел в математике позволяет решать сложные задачи, которые не могут быть решены с помощью действительных чисел. Они являются мощным инструментом, который активно применяется не только в математике, но и во многих других областях науки и техники.
Применение комплексных чисел в физике и технике

В области электрических цепей комплексные числа используются для описания переменного тока и переменного напряжения. Сочетание действительной и мнимой частей комплексных чисел позволяет учитывать как активную (потеряную), так и реактивную (хранящуюся в энергетических элементах) составляющие электрической цепи.
Также комплексные числа применяются в анализе электрических и магнитных полей. С помощью комплексных чисел можно описать амплитуду и фазу переменных полей, а также вычислить их значения в различных точках пространства. К примеру, комплексное представление позволяет анализировать процессы распространения электромагнитных волн, в том числе радиоволн, микроволн и световых волн.
Необходимо отметить, что комплексные числа также имеют широкое применение в области сигнальной обработки и передачи данных. Они используются, например, при модуляции сигналов, кодировании и декодировании данных, анализе спектра сигналов и многое другое.
В области техники комплексные числа применяются во многих областях, таких как контроль и регулирование систем, описание и анализ электрических и механических колебаний, расчеты в схемотехнике и электронике, моделирование и анализ физических процессов и технических систем.
Общее применение комплексных чисел в физике и технике связано с их способностью описывать и учитывать фазовые сдвиги, амплитуды и периодические процессы. Благодаря этому комплексные числа становятся мощным инструментом для решения различных задач и анализа сложных систем.
Решение квадратного уравнения с комплексными корнями

Если дискриминант D = b^2 - 4ac меньше нуля, то квадратное уравнение имеет комплексные корни. В этом случае корни могут быть найдены с использованием комплексных чисел.
Для решения квадратного уравнения с комплексными корнями применяются следующие шаги:
| Шаг | Действие |
|---|---|
| 1 | Вычислите дискриминант D = b^2 - 4ac. |
| 2 | Если D |
| 3 | Найдите комплексные корни уравнения с использованием формулы: |
| x = ( -b ± √D ) / ( 2a ) , где √D - квадратный корень из D. | |
| Обратите внимание, что комплексные корни представляются в виде x = a + bi, где a и b - действительные числа, а i - мнимая единица (i^2 = -1). | |
| Таким образом, корни будут иметь вид: | |
| x1 = ( -b + √D ) / ( 2a) | |
| x2 = ( -b - √D ) / ( 2a) |
Например, рассмотрим квадратное уравнение x^2 + x + 1 = 0.
Дискриминант этого уравнения равен: D = 1 - 4 * 1 * 1 = -3.
Так как D
Применяя формулу, получаем:
x1 = ( -1 + √(-3) ) / ( 2 * 1 ) = ( -1 + i√3 ) / 2
x2 = ( -1 - √(-3) ) / ( 2 * 1 ) = ( -1 - i√3 ) / 2
Таким образом, корни квадратного уравнения x^2 + x + 1 = 0 равны x1 = ( -1 + i√3 ) / 2 и x2 = ( -1 - i√3 ) / 2.
Графическое представление комплексных чисел на плоскости
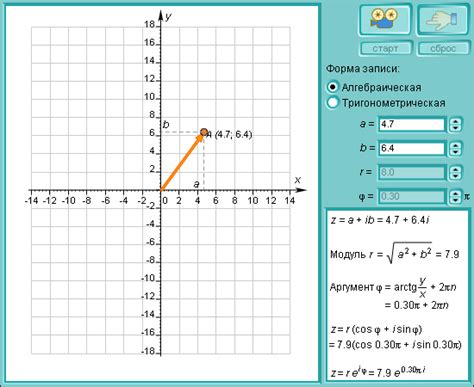
Комплексная плоскость представляет собой двумерную плоскость, где горизонтальная ось обозначает действительные числа, а вертикальная ось – мнимые числа. Точка на комплексной плоскости представляет комплексное число вида a + bi.
При графическом представлении комплексного числа его действительная часть обычно обозначается координатой по горизонтальной оси, а мнимая – координатой по вертикальной оси. Таким образом, легко можно визуально определить действительную и мнимую части комплексного числа.
Также на комплексной плоскости можно указать аргумент комплексного числа, который показывает угол между положительным направлением действительной оси и линией, соединяющей начало координат и комплексное число. Модуль комплексного числа, то есть его абсолютное значение, можно определить как расстояние от начала координат до точки, соответствующей комплексному числу.
Графическое представление комплексных чисел на плоскости позволяет удобно выполнять операции с комплексными числами, такие как сложение, вычитание, умножение и деление. Оно также находит применение в различных областях науки и техники, таких как электротехника, физика, теория сигналов и др.
Примеры применения комплексных чисел в реальной жизни

Электрические цепи
Комплексные числа широко используются в электрических цепях. Они позволяют описывать фазовые сдвиги и импеданс, что позволяет разрабатывать и анализировать сложные электрические системы, такие как сети передачи энергии, электронные схемы и сети связи.
Квантовая механика
В квантовой механике комплексные числа играют важную роль. Волновая функция, описывающая состояние частицы в квантовой системе, является комплексной функцией. Комплексные числа используются для описания вероятности нахождения частицы в определенном состоянии и для описания суперпозиций состояний.
Анализ колебаний и волн
Комплексные числа играют важную роль в анализе колебаний и волн. Они позволяют представить гармонические колебания, такие как звук и электромагнитные волны, с помощью комплексных функций. Комплексные числа также позволяют анализировать спектральную структуру и фазовые свойства колебаний.
Статистика и вероятность
Комплексные числа также могут быть использованы для описания статистических систем и вероятности. Комплексные числа позволяют описывать случайные переменные векторами в комплексном пространстве. Это может быть полезно, например, при анализе случайных процессов и моделировании вероятностных распределений.
Сигнальная обработка
Комплексные числа широко используются в области сигнальной обработки для анализа и обработки временных и частотных сигналов. Комплексные числа позволяют представить сигналы в комплексном пространстве, что упрощает анализ и обработку их спектральной структуры.
Это лишь некоторые примеры применения комплексных чисел в реальной жизни. Они также находят применение в других областях, таких как физика, инженерия, экономика и системы управления.



