Треугольник - это одна из основных геометрических фигур, которая имеет огромное значение в математике. Изучение треугольников помогает понять и применять различные формулы и свойства, которые необходимы для решения задач в различных областях. Формулы треугольника позволяют определить его площадь, периметр, а также длины сторон и углы.
Формула площади треугольника - одна из наиболее известных и используемых формул в математике. Площадь треугольника можно найти, зная длины двух его сторон и величину угла между ними. В зависимости от известных данных применяются различные формулы: для прямоугольного треугольника, равнобедренного треугольника и т.д.
Свойства треугольника также играют важную роль в решении геометрических задач. Одним из основных свойств треугольника является то, что сумма всех его внутренних углов равна 180 градусам. Это свойство называется суммой углов треугольника и позволяет находить неизвестные углы, зная значения других.
...
Основные свойства треугольника в математике

1. Сумма углов треугольника:
В любом треугольнике сумма всех его внутренних углов равна 180 градусам. То есть:
Угол A + Угол B + Угол C = 180°
2. Неравенство двух углов треугольника:
Сумма двух углов треугольника всегда больше третьего угла. Другими словами:
Угол A + Угол B > Угол C
Угол B + Угол C > Угол A
Угол A + Угол C > Угол B
3. Соотношение между сторонами и углами:
В прямоугольном треугольнике гипотенуза (самая длинная сторона) является противолежащей главному углу (прямому углу) и всегда больше остальных двух сторон.
В остроугольном треугольнике каждая из сторон меньше суммы двух других сторон.
В тупоугольном треугольнике одна из сторон больше суммы двух других сторон.
4. Теорема Пифагора:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин других двух сторон. Это можно записать следующим образом:
с² = a² + b²
5. Формулы для нахождения площади треугольника:
Площадь треугольника можно найти, используя различные формулы в зависимости от имеющихся данных:
а) Если известны длины всех трех сторон треугольника (a, b, c), то площадь можно найти по формуле Герона:
S = √(p(p-a)(p-b)(p-c))
где p = (a + b + c)/2 - полупериметр треугольника.
б) Если известны длины стороны треугольника (a) и высота, проведенная к этой стороне (h), то площадь можно найти по формуле:
S = (a * h)/2
6. Формулы для нахождения периметра треугольника:
Периметр треугольника можно найти, просто сложив длины всех его сторон:
P = a + b + c
Формулы для вычисления площади, периметра и углов треугольника
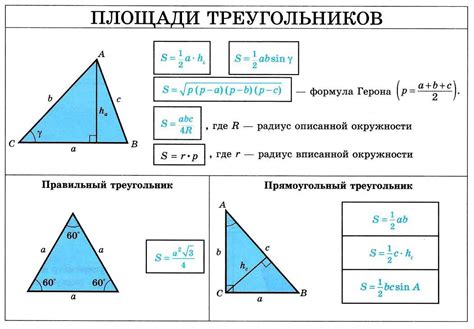
Площадь треугольника:
- По формуле Герона:
- По формуле для прямоугольного треугольника:
С помощью данной формулы можно вычислить площадь треугольника, зная длины его сторон. Формула выглядит следующим образом:
S = sqrt(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, a, b, c - длины сторон треугольника, p - полупериметр треугольника (p = (a + b + c) / 2).
Если треугольник является прямоугольным, то его площадь можно вычислить по формуле:
S = (a * b) / 2,
где S - площадь треугольника, a, b - длины катетов.
Периметр треугольника:
Периметр треугольника вычисляется путем сложения длин всех его сторон:
P = a + b + c,
где P - периметр треугольника, a, b, c - длины сторон треугольника.
Углы треугольника:
Треугольник имеет три угла, обозначаемых символами A, B и C. Сумма углов треугольника равна 180 градусов:
A + B + C = 180°.
Также существуют различные формулы для вычисления значений углов треугольника. Например:
- Для прямоугольного треугольника:
- Для равнобедренного треугольника:
- Для разностороннего треугольника:
Угол С равен 90 градусов.
Если треугольник равнобедренный (два равных угла и две равные стороны), то третий угол можно вычислить по формуле:
Угол С = 180° - 2 * A,
где A - значение равных углов треугольника.
В этом случае вычисление значений углов треугольника может производиться с помощью закона косинусов или закона синусов.
Знание формул для вычисления площади, периметра и углов треугольника является важной основой в геометрии и математике в целом.
Применение треугольников в различных областях науки и техники

Одним из основных применений треугольников является измерение расстояний и вычисление площадей. С помощью формулы Герона можно вычислить площадь любого треугольника, зная длины его сторон. Это очень полезно, например, для архитекторов и инженеров при планировании и строительстве зданий и мостов.
Треугольники также используются для решения задач оптики. Линзы и зеркала имеют форму треугольников или их частей, что позволяет управлять лучами света и фокусировать их в определенные точки. Это фундаментальное свойство треугольников используется в оптических приборах, таких как микроскопы, телескопы и фотокамеры.
В астрономии треугольники используются для измерения расстояний до звезд и планет. Метод параллакса основан на измерении изменения угла между двумя наблюдателями на земле и звездой. Это позволяет определить расстояние до объекта на небесной сфере. Также треугольники применяются для моделирования траекторий и расчета орбит спутников и планет.
Треугольники используются в компьютерной графике для рендеринга трехмерных моделей и расчета их освещения. Помимо этого, они используются в алгоритмах компьютерного зрения для обнаружения и измерения объектов на изображениях.
Другим применением треугольников является анализ данных. В математической статистике треугольники используются для построения доверительных интервалов и проведения статистических тестов. Также они применяются при решении задач оптимизации и моделирования.



