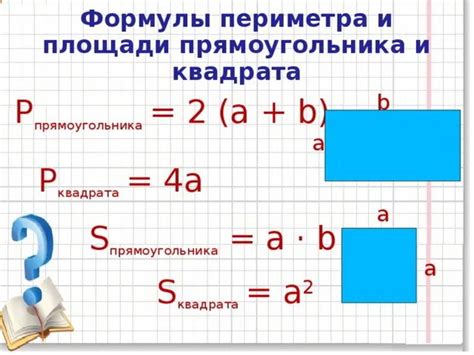
Квадрат – это геометрическая фигура, имеющая все стороны равными. Это одна из самых простых и изучаемых фигур в математике. Она имеет много применений как в повседневной жизни, так и в различных областях науки. Один из основных параметров квадрата – площадь. Площадь квадрата определяется как произведение длины его стороны на саму себя. Например, если сторона квадрата равна 6 см, то его площадь составит 36 квадратных сантиметров.
Однако помимо площади, очень важным параметром квадрата является его периметр. Периметр – это сумма длин всех сторон квадрата. Так как все стороны квадрата равны между собой, то периметр можно вычислить, умножив длину одной стороны на 4. Например, если длина стороны квадрата равна 6 см, то его периметр будет равен 24 сантиметра.
Формула для вычисления площади квадрата: S = a2, где S – площадь, а – длина стороны квадрата.
Что такое площадь квадрата?
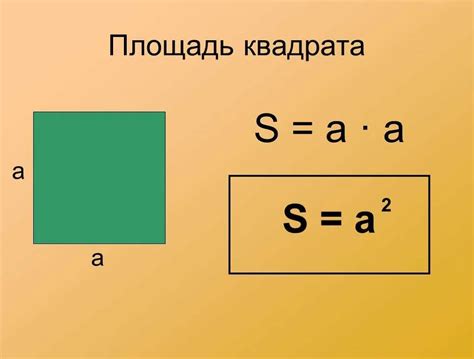
Формула для расчета площади квадрата:
| Формула | Пример |
|---|---|
| Площадь = Сторона^2 | Площадь = 6^2 = 36 см^2 |
В данной формуле "Сторона" обозначает длину стороны квадрата. В нашем примере, если сторона квадрата составляет 6 см, то его площадь равна 36 квадратным сантиметрам.
Важно помнить, что единицы измерения площади квадрата указываются в квадратных единицах длины.
По формуле для площади квадрата также можно рассчитать длину его стороны, если известна площадь. Для этого необходимо извлечь квадратный корень из площади. Например, если площадь квадрата составляет 36 см^2, то его сторона будет равна 6 см.
Как вычислить площадь квадрата 36 см?
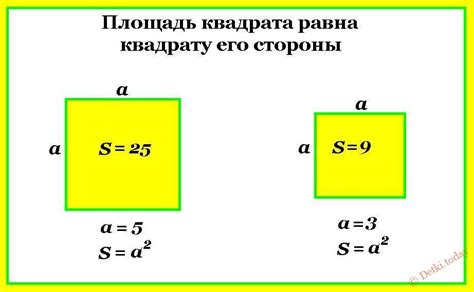
Для вычисления площади квадрата необходимо знать длину его стороны. В данном случае сторона квадрата равна 36 см, поэтому мы можем просто возвести эту длину в квадрат.
Формула для вычисления площади квадрата выглядит следующим образом:
S = a2
где S - площадь квадрата, а a - длина стороны квадрата.
Подставляя в формулу значение, получаем:
S = 362
Таким образом, площадь квадрата 36 см равна 1296 квадратным сантиметрам.
Формула расчета площади квадрата

Площадь квадрата можно вычислить с использованием простой формулы. Для этого необходимо знать длину стороны квадрата. Формула расчета площади квадрата выглядит следующим образом:
S = a^2
Где S - площадь квадрата, а - длина стороны.
Например, если длина стороны квадрата равна 6 см, то площадь квадрата будет:
S = 6^2 = 36 см^2
Таким образом, площадь квадрата с длиной стороны 6 см составляет 36 квадратных сантиметров.
Примеры расчета площади квадрата 36 см
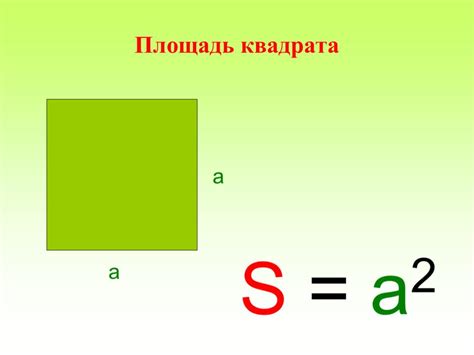
Для расчета площади квадрата, если известна его сторона, нужно возвести ее в квадрат.
В данном случае известно, что периметр квадрата равен 36 см, и нужно найти его площадь.
Периметр квадрата вычисляется по формуле P = 4 * a, где а - длина стороны квадрата.
Для данного примера, периметр равен 36 см, значит, a = 36 / 4 = 9 см.
Теперь, чтобы найти площадь квадрата, нужно возвести длину его стороны в квадрат: S = a^2, где а - длина стороны.
Подставив значение a = 9 см в формулу, получим: S = 9^2 = 81 см².
Итак, площадь квадрата со стороной 9 см равна 81 см².
Данный пример показывает, как можно вычислить площадь квадрата, если известен его периметр.
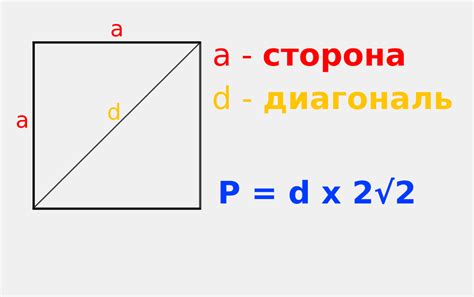
Что такое периметр квадрата?

Для квадрата со стороной S формула для расчета периметра будет следующей:
| Периметр квадрата (P) | = | 4 * S |
Например, если известна длина стороны квадрата и она равна 9 см, то его периметр будет равен:
| Периметр (P) | = | 4 * 9 | = | 36 см |
Таким образом, периметр квадрата со стороной 9 см равен 36 см.
Как вычислить периметр квадрата?
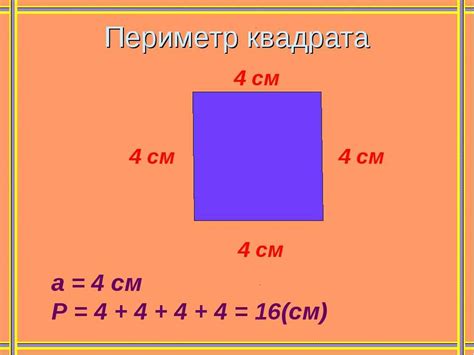
Периметр квадрата = 4 * сторона квадрата
Где сторона квадрата - это длина одной из его сторон.
Давайте рассмотрим пример вычисления периметра квадрата, если известна его площадь. Допустим, площадь квадрата равна 36 квадратным сантиметрам. Чтобы найти длину стороны квадрата, можно извлечь квадратный корень из площади:
Длина стороны квадрата = квадратный корень из площади
В нашем случае, длина стороны квадрата будет равна:
Длина стороны квадрата = √36 = 6 сантиметров
Теперь, мы можем вычислить периметр квадрата, используя найденную длину стороны:
Периметр квадрата = 4 * 6 = 24 сантиметра
Итак, периметр квадрата с площадью 36 квадратных сантиметров равен 24 сантиметрам.
Формула расчета периметра квадрата
| Формула: | Периметр квадрата = 4 * длина стороны |
Для примера, если известно, что площадь квадрата составляет 36 квадратных сантиметров, то мы можем найти длину стороны, используя формулу для расчета площади квадрата:
| Дано: | Площадь квадрата = 36 см² |
| Решение: | Длина стороны = √площадь квадрата |
| Длина стороны = √36 см² | |
| Длина стороны = 6 см |
Теперь, когда у нас есть длина стороны, мы можем использовать формулу для расчета периметра квадрата:
| Дано: | Длина стороны = 6 см |
| Решение: | Периметр квадрата = 4 * длина стороны |
| Периметр квадрата = 4 * 6 см | |
| Периметр квадрата = 24 см |
Таким образом, при условии, что площадь квадрата составляет 36 сантиметров квадратных, периметр квадрата будет равен 24 сантиметрам.
Примеры расчета периметра квадрата
Периметр квадрата можно рассчитать, зная значение стороны. Формула для расчета периметра квадрата проста: нужно умножить значение стороны на 4.
Пример 1:
Допустим, у нас есть квадрат со стороной 5 см. Чтобы найти периметр, нужно умножить 5 на 4:
Периметр = 5 см * 4 = 20 см
Таким образом, периметр квадрата со стороной 5 см будет равен 20 см.
Пример 2:
Пусть у нас есть квадрат с стороной 10 см. Чтобы найти периметр, нужно умножить 10 на 4:
Периметр = 10 см * 4 = 40 см
Периметр квадрата со стороной 10 см будет равен 40 см.
Таким образом, зная значение стороны квадрата, можно легко найти его периметр, применяя формулу периметра квадрата.



