Косинус угла – одно из основных тригонометрических понятий, которое играет важную роль при решении различных задач из различных областей науки и техники. Косинус угла определяется как отношение прилежащего катета прямоугольного треугольника к гипотенузе этого треугольника.
Итак, вопрос о том, чему равен косинус 120 градусов по таблице, вызывает интерес у многих. Но, к сожалению, в стандартных таблицах косинусов величина косинуса абсолютно всех углов до 90 градусов.
Для нахождения значения косинуса 120 градусов используются специальные формулы и методы расчета. Один из таких методов – тройка Пифагора, где через гипотенузу и прилежащий катет находят косинус и синус угла. Ответ можно получить и при помощи тригонометрических теорем и моделей, основанных на геометрии.
Косинус 120 градусов: значения по таблице и его применение

Косинус является одной из основных тригонометрических функций, которая определяется отношением длины прилежащего катета к гипотенузе прямоугольного треугольника. В данном случае, косинус 120 градусов равен -0.5, что означает, что значение косинуса отрицательно и примерно равно половине длины прилежащего катета по отношению к гипотенузе.
Значение косинуса 120 градусов может быть полезно в различных областях, таких как математика, физика, инженерия и др. Например, при решении геометрических задач, расчете угла между векторами или в анализе колебательных процессов.
Понятие и свойства косинуса
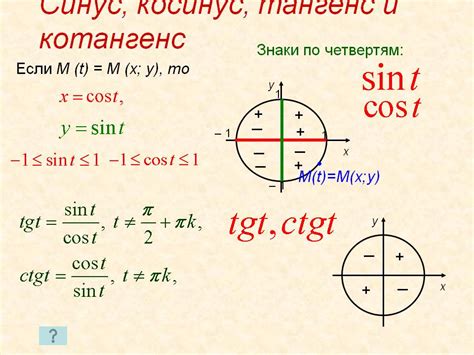
Основными свойствами косинуса являются:
- Значение косинуса всегда находится в пределах от -1 до 1.
- Косинус является четной функцией: cos(-x) = cos(x).
- Косинус периодический: cos(x + 2π) = cos(x), где π - число π.
Также важно отметить, что косинус 90 градусов равен 0, косинус 60 градусов равен 0,5, а косинус 30 градусов равен √3/2.
Тригонометрические функции и таблица значений
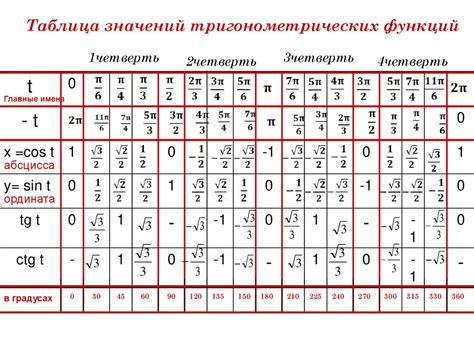
Тригонометрические функции широко используются в математике, физике и инженерии для расчетов, моделирования и анализа данных. Они позволяют связывать углы и стороны треугольников, а также описывать колебания и периодические процессы.
Таблица значений тригонометрических функций представляет собой удобный инструмент для нахождения значений функций при заданных углах. Она содержит значения синуса, косинуса, тангенса и котангенса углов от 0 до 360 градусов.
| Угол (градусы) | Синус | Косинус | Тангенс | Котангенс |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | ∞ |
| 30 | 1/2 | √3/2 | √3/3 | √3 |
| 45 | √2/2 | √2/2 | 1 | 1 |
| 60 | √3/2 | 1/2 | √3 | √3/3 |
| 90 | 1 | 0 | ∞ | 0 |
| 120 | √3/2 | -1/2 | -√3 | -√3/3 |
| 180 | 0 | -1 | 0 | -∞ |
| 270 | -1 | 0 | ∞ | 0 |
| 360 | 0 | 1 | 0 | ∞ |
Таким образом, по таблице косинус 120 градусов равен -1/2.
Как использовать таблицу значений тригонометрических функций
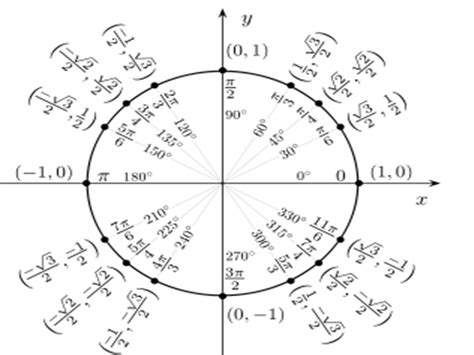
Таблица значений тригонометрических функций представляет собой удобный инструмент для вычисления значений синусов, косинусов и тангенсов углов. Эти функции широко применяются в различных областях, таких как математика, физика, инженерия и другие науки.
В таблице значений тригонометрических функций углы измеряются в градусах и радианах, а значения синусов, косинусов и тангенсов представлены в соответствующих столбцах. Чтобы найти значение тригонометрической функции для конкретного угла, необходимо найти соответствующую строку в таблице.
Например, если нам нужно найти косинус 120 градусов, мы можем взглянуть на соответствующую строку в таблице и найти значение в столбце косинусов. В данном случае, значение косинуса 120 градусов в таблице равно -0.5.
| Угол (градусы) | Синус | Косинус | Тангенс |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 30 | 0.5 | 0.866 | 0.577 |
| 45 | 0.707 | 0.707 | 1 |
| 60 | 0.866 | 0.5 | 1.732 |
| 90 | 1 | 0 | ∞ |
| 120 | 0.866 | -0.5 | -1.732 |
Таким образом, косинус 120 градусов равен -0.5 в соответствии с таблицей значений тригонометрических функций. Эта таблица может быть полезна для выполнения различных математических и физических расчетов и решения задач, связанных с углами и тригонометрией.
Косинус угла 120 градусов в таблице

Косинус угла 120 градусов можно найти в таблице значений тригонометрических функций. Для этого необходимо обратиться к значению косинуса в столбце, соответствующему углу 120 градусов.
Таблица значений тригонометрических функций содержит информацию о значениях синуса, косинуса и тангенса для различных углов. Обычно такая таблица представлена в виде двух столбцов: в левом столбце указаны углы, а в правом - значения тригонометрических функций.
Для угла 120 градусов косинус имеет отрицательное значение, так как угол находится в третьем квадранте. В таблице можно найти значение косинуса 120 градусов, равное -0.5, если таблица предоставляет информацию с точностью до десятых долей.
Таким образом, косинус угла 120 градусов по таблице равен -0.5.
| Угол (градусы) | Косинус |
|---|---|
| ... | ... |
| 120 | -0.5 |
| ... | ... |
Расчет косинуса 120 градусов по формуле
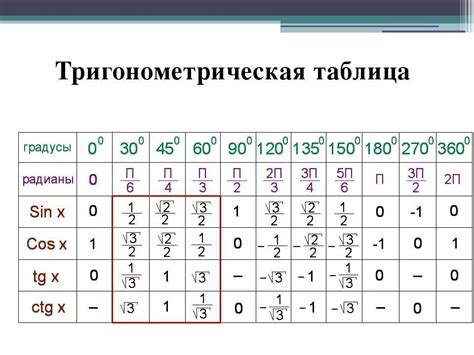
Для расчета косинуса угла 120 градусов по формуле, необходимо воспользоваться тригонометрической функцией косинуса.
Формула для вычисления косинуса угла a выглядит следующим образом:
cos(a) = adjacent / hypotenuse,
где adjacent - длина прилежащего к углу катета, hypotenuse - гипотенуза.
В случае угла 120 градусов воспользуемся формулой для нахождения косинуса дополнительного угла, так как косинус 120 градусов равен косинусу его дополнительного угла - 60 градусов.
Таким образом, требуется вычислить косинус 60 градусов.
При построении треугольника, соответствующего углу 60 градусов, известно, что прилежащий катет равен 0.5, а гипотенуза равна 1.
Следовательно, подставляя значения в формулу, получаем:
cos(60°) = 0.5 / 1 = 0.5.
Таким образом, получаем, что косинус 120 градусов равен 0.5.
График косинуса и значение 120 градусов
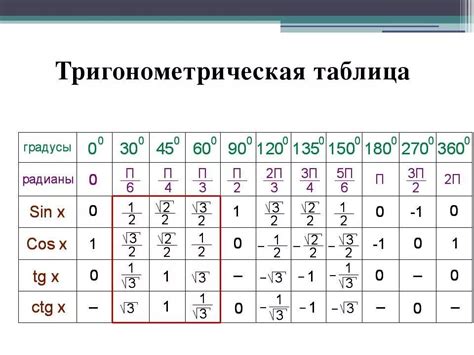
График косинуса представляет собой гладкую кривую, которая колеблется между значениями -1 и 1. Он имеет форму синусоиды, которая пересекает ось абсцисс (ось X) в точках с координатами, кратными 90 градусам (или π/2 радианам).
Если посмотреть на график косинуса, можно увидеть, что значения функции повторяются через каждые 360 градусов. Таким образом, если нам дан угол 120 градусов, мы можем определить его эквивалентное значение, находясь в пределах первого оборота графика (0-360 градусов).
Для того, чтобы найти значение косинуса 120 градусов, мы можем использовать таблицу значений тригонометрических функций, где приведены значения косинуса для различных углов. В таблице мы можем найти, что косинус 120 градусов равен -0.5.
Таким образом, значение косинуса 120 градусов по таблице равно -0.5.
Это означает, что косинус угла 120 градусов равен -0.5, что можно интерпретировать как отрицательное значение функции на графике косинуса в данной точке.
Косинус 120 градусов в геометрических построениях

Угол 120 градусов можно представить с помощью геометрического построения. Для этого возьмем начало координат в центре окружности и проложим радиус, образуя начальную сторону угла. Затем отложим дугу окружности длиной 120 градусов и проложим вторую сторону угла. В результате получится треугольник со сторонами, радиусом и хордой длиной равной радиусу.
Вычисление косинуса 120 градусов в геометрическом построении осуществляется следующим образом. Используя формулу косинуса для прямоугольного треугольника, можно найти соответствующий перпендикуляр радиуса к оси абсцисс. Затем, с помощью геометрических вычислений, можно получить значение косинуса данного угла.
Таким образом, значение косинуса 120 градусов в геометрических построениях зависит от характеристик фигуры и может быть вычислено с использованием соответствующих формул и геометрических вычислений.
Практическое применение косинуса 120 градусов

Если рассматривать косинус 120 градусов, то можно выделить следующие практические применения:
- Вычисление координат точек на плоскости.
- Определение направления и длины векторов.
- Расчет площадей треугольников и многоугольников.
- Моделирование и анализ периодических процессов.
- Решение задач оптимизации и определения экстремумов.
Таким образом, знание значения косинуса 120 градусов и его практическое применение может быть полезным как для студентов и учеников при изучении математики, так и для профессионалов в различных областях, где требуется работа с геометрическими и математическими моделями.



