Прямоугольник – это особый вид четырехугольника, который имеет следующие характеристики: все его углы равны 90 градусам, а противоположные стороны равны. Также прямоугольник может быть определен через свойства его диагоналей – отрезков, соединяющих противоположные вершины.
Для доказательства равенства диагоналей в прямоугольнике, воспользуемся свойствами этой фигуры и геометрическими соображениями. Рассмотрим некоторый произвольный прямоугольник. Обозначим его вершины точками A, B, C и D. Соединим точки A и C отрезком. Пусть точка пересечения диагоналей будет обозначена буквой O.
Чтобы доказать равенство диагоналей, рассмотрим треугольники AOB и COD. По определению прямоугольника, углы AOB и COD равны 90 градусам. Также, по свойству прямоугольника, сторона AB равна стороне CD и сторона AO равна стороне CO. Исходя из этих соответствий и свойств равенства углов, мы можем заключить, что треугольники AOB и COD равны. Следовательно, диагонали AC и BD в прямоугольнике равны между собой.
Четырехугольник называется прямоугольником?

Чтобы доказать, что диагонали прямоугольника равны, рассмотрим треугольник, образованный диагоналями. Пусть AB и CD - диагонали прямоугольника ABCD.
Используя свойства прямоугольника, мы можем утверждать, что AD и BC - это пары параллельных сторон прямоугольника.
Так как AD и BC параллельны и AB и CD параллельны, по свойству параллельных линий, мы можем утверждать, что углы A и C равны, а также углы B и D равны.
Таким образом, получен треугольник ACD с тремя равными углами, а значит, он является равнобедренным треугольником. В равнобедренном треугольнике стороны, противоположные равным углам, равны.
В нашем случае сторона AD равна стороне BC, и сторона CD равна стороне AB.
Таким образом, диагонали прямоугольника являются равными.
Определение прямоугольника
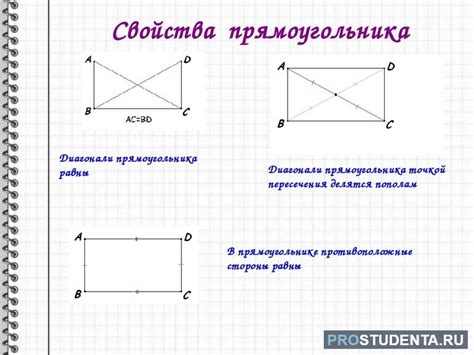
Прямоугольник можно также определить как частный случай параллелограмма, у которого все углы равны 90 градусам.
Высота прямоугольника является отрезком, перпендикулярным основанию и соединяющим его середину с противоположной стороной.
Основание прямоугольника - это одна из его сторон, на которой лежит высота.
Диагонали прямоугольника являются отрезками, соединяющими противоположные вершины.
Докажем, что диагонали прямоугольника являются равными:
- Пусть AB и CD - стороны прямоугольника, а AC и BD - его диагонали.
- По свойству прямоугольника, стороны AB и CD перпендикулярны.
- Из свойств перпендикуляров следует, что угол A и угол C являются прямыми.
- Таким образом, треугольники ABC и CDA являются прямоугольными.
- Также, по свойству прямоугольника, угол A равен углу C, и угол B равен углу D.
- Треугольники ABC и CDA имеют по два равных угла и общую сторону AC.
- Треугольники ABC и CDA равны (по критерию равенства двух треугольников).
- Из равенства треугольников ABC и CDA следует, что сторона BC равна стороне AD.
- Таким образом, диагонали AC и BD прямоугольника равны друг другу.
Прямоугольник и его особенности
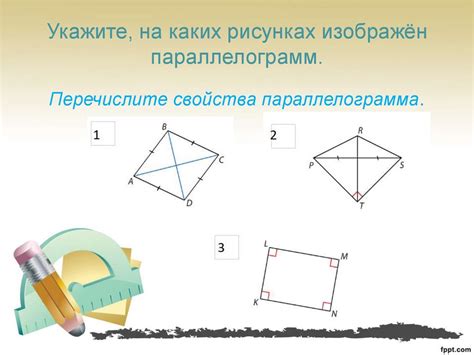
Основные особенности прямоугольника:
- Углы: Все углы прямоугольника равны 90 градусам. Такое свойство делает его идеальным для построения квадратных и прямоугольных форм.
- Стороны: Прямоугольник имеет две пары параллельных сторон. Эти пары сторон равны по длине, что делает прямоугольник симметричным.
- Диагонали: Диагонали прямоугольника имеют одинаковую длину. Это может быть доказано с помощью различных способов, например через теорему Пифагора, с использованием свойств подобных треугольников или методом моментов.
Доказательство равенства диагоналей прямоугольника может быть представлено следующим образом:
Пусть ABCD - прямоугольник, AC и BD - его диагонали. Требуется доказать, что AC = BD.
Рассмотрим треугольники ABC и ADC. Они являются прямоугольными, так как углы ABC и ADC равны 90 градусам.
Они также являются равнобедренными, так как стороны AB и AD равны прямоугольнику AD и AD и углы ABC и ADC равны 90 градусам. Следовательно, углы BAC и DAC равны по мере BS=DS и углы ACD и BCD равны по мере CS=AS.
Таким образом, треугольники ABC и ADC подобны, поскольку у них одинаковая форма и соответствующие углы равны.
Отсюда следует, что соотношение между их сторонами также будет одинаковым, то есть AB/AC = BC/DC = AD/AC.
Следовательно, мы можем сказать, что AB = DC и AD = BC.
Наконец, складывая равенства AB = DC и AD = BC, мы получаем AB + AD = DC + BC.
Таким образом, AC = BD, что доказывает, что диагонали прямоугольника равны.
Как доказать, что четырехугольник является прямоугольником?
- Проверить, что все углы четырехугольника равны. Для этого можно измерить каждый угол с помощью транспортира или использовать специальные инструменты для измерения углов.
- Убедиться, что все углы четырехугольника равны 90 градусов. Для этого можно использовать теорему о сумме углов в четырехугольнике, которая гласит, что сумма углов в любом четырехугольнике равна 360 градусов. Если все углы равны и их сумма составляет 360 градусов, то каждый угол четырехугольника равен 90 градусов.
Равенство диагоналей
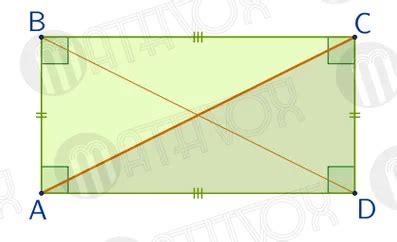
Для доказательства равенства диагоналей в прямоугольнике можно воспользоваться свойствами этой фигуры. Итак, пусть ABCD - это прямоугольник, где AB и CD - это стороны, а AC и BD - это диагонали.
Для начала, заметим, что в прямоугольнике AC и BD являются биссектрисами сторон AB и CD. Из этого следует, что треугольники ABC и ADC равнобедренные, поскольку биссектриса каждому из них делит угол при основании пополам.
Также, учитывая свойства прямоугольника, сторона AB параллельна стороне CD, и сторона BC параллельна стороне AD. Из этого следует, что углы ABC и CDA также равны, так как они соответственно противоположные.
Теперь мы можем применить свойства равнобедренных треугольников. В треугольниках ABC и ADC углы ABC и CDA равны, и углы BAC и CDA также равны (так как дополнительны). Следовательно, треугольники ABC и ADC равны между собой по двум сторонам и углу.
Таким образом, по теореме о равенстве треугольников, стороны AB и CD равны, а углы при основании ABC и CDA также равны. Из этого следует, что прямоугольник ABCD является параллелограммом с равными сторонами и углами при основании. В параллелограмме диагонали всегда равны, поэтому в прямоугольнике AC и BD также равны.
Способы доказательства равенства диагоналей
Для доказательства равенства диагоналей прямоугольника существуют несколько способов. Ниже приведены два основных способа, которые наиболее часто используются в геометрии.
1. Использование свойств прямоугольника.
Прямоугольник характеризуется следующими свойствами:
- У прямоугольника все углы равны 90 градусам;
- Противоположные стороны прямоугольника параллельны;
- Диагонали прямоугольника перпендикулярны и равны между собой.
2. Использование координатной геометрии.
Можно использовать координатную геометрию для доказательства равенства диагоналей прямоугольника, используя формулы расстояния между точками.
Пусть A(x1, y1) и C(x2, y2) - вершины прямоугольника, а B(x3, y3) и D(x4, y4) - середины сторон AC и BD соответственно. Расстояния между точками можно найти по формулам:
AB = sqrt((x2-x1)^2 + (y2-y1)^2)
CD = sqrt((x4-x3)^2 + (y4-y3)^2)
Если AB = CD, то диагонали прямоугольника равны между собой.
Оба эти способа позволяют доказать равенство диагоналей прямоугольника и использовать его свойства в решении геометрических задач.
Метод с использованием свойств прямоугольника

Для доказательства того, что диагонали прямоугольника равны, можно воспользоваться его свойствами.
Пусть дан прямоугольник ABCD, где AB и CD - его стороны, а AC и BD - его диагонали.
Свойство 1: В прямоугольнике противоположные стороны равны. Поэтому AB = CD.
Свойство 2: В прямоугольнике все углы прямые. Таким образом, угол BAD и угол CBA являются прямыми углами.
Свойство 3: В любом треугольнике, у которого один угол прямой, диагональ является гипотенузой, а две стороны становятся катетами. Из этого следует, что треугольники ABD и BAC являются прямоугольными.
Свойство 4: В прямоугольном треугольнике гипотенуза является самой длинной стороной, а катеты - короче гипотенузы. Применительно к нашему прямоугольнику это означает, что диагональ AC является самой длинной стороной треугольника ABD, а диагональ BD - самой длинной стороной треугольника BAC.
Итак, поскольку в прямоугольнике все стороны равны, то AB=CD, следовательно, треугольники ABD и BAC равнобедренные. А так как в этих треугольниках диагонали являются боковыми сторонами, то это означает, что AC = BD.
Таким образом, доказано, что диагонали прямоугольника равны друг другу.
Метод с использованием координат
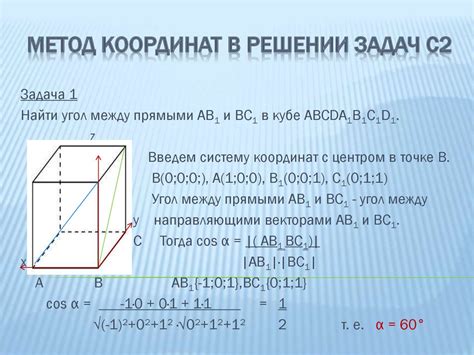
Для доказательства, что диагонали прямоугольника равными, можно использовать метод с использованием координат. Для этого рассмотрим прямоугольник ABCD с вершинами A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) и D(x₄, y₄).
Расстояние между двуми точками (x₁, y₁) и (x₂, y₂) на плоскости можно вычислить с помощью формулы:
AB = √((x₂ - x₁)² + (y₂ - y₁)²)
AC = √((x₃ - x₁)² + (y₃ - y₁)²)
BD = √((x₄ - x₂)² + (y₄ - y₂)²)
CD = √((x₄ - x₃)² + (y₄ - y₃)²)
Докажем, что диагональ AC равна диагонали BD:
Сравним квадраты длин этих диагоналей:
AC² = (x₃ - x₁)² + (y₃ - y₁)²
BD² = (x₄ - x₂)² + (y₄ - y₂)²
Подстановкой соответствующих координат можно убедиться, что AC² = BD²:
(x₃ - x₁)² + (y₃ - y₁)² = (x₄ - x₂)² + (y₄ - y₂)²
Следовательно, диагонали AC и BD прямоугольника равными.
Таким образом, данный метод доказывает, что в прямоугольнике диагонали равными.
Теоремы и правила, помогающие доказать равенство диагоналей
| 1. | В прямоугольнике противоположные стороны параллельны и равны между собой. Таким образом, сторона, opposite to диагональ, параллельна диагональ. |
| 2. | В прямоугольнике все стороны равны, поэтому его диагонали равны по определению. |
| 3. | Прямоугольник можно разразить на два прямоугольных треугольника по диагонали, которые являются равнобедренными. В равнобедренном треугольнике диагонали, проведенные из вершины с равными углами, равны между собой. Применительно к прямоугольнику это означает, что его диагонали равны. |
Как видно из этих теорем и правил, доказательство равенства диагоналей в прямоугольнике основано на его геометрических свойствах и определениях.
Применение равенства диагоналей в геометрических задачах
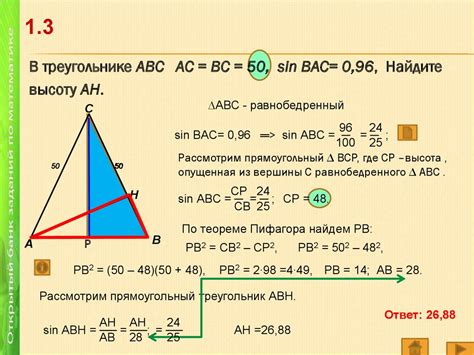
Равенство диагоналей прямоугольника может быть использовано в различных геометрических задачах. Например, при доказательстве свойств прямоугольника, с использованием равенства диагоналей, можно установить следующие факты:
| Свойство | Доказательство |
|---|---|
| Диагонали делят прямоугольник на четыре равных треугольника | Равенство диагоналей дает возможность разделить прямоугольник на два равных прямоугольных треугольника. Каждая диагональ является гипотенузой в одном из этих треугольников, а стороны прямоугольника - катетами. |
| Сумма квадратов длин сторон прямоугольника равна квадрату длины диагоналей | Используя теорему Пифагора для каждого из четырех треугольников, образованных диагоналями и сторонами прямоугольника, можно показать, что сумма квадратов длин сторон равна квадрату длины диагоналей. |
| Диагонали являются биссектрисами углов прямоугольника | Так как диагонали делят прямоугольник на два равных треугольника, то они являются биссектрисами углов этих треугольников. Следовательно, диагонали также являются биссектрисами углов прямоугольника. |
Таким образом, равенство диагоналей в прямоугольнике предоставляет нам много информации о его свойствах и позволяет использовать ее при решении геометрических задач.



