В математике, решение уравнений часто требует нахождения неизвестных значений. Одна из таких задач заключается в определении числа, на которое нужно умножить 15, чтобы получить 100. Казалось бы, для решения данной проблемы потребуется выполнить длительные вычисления, однако существует простой и быстрый способ найти ответ.
Для начала, давайте представим задачу в виде уравнения:
15 * X = 100
где 15 - число, которое необходимо умножить на Х, чтобы получить 100.
Теперь, чтобы найти значение Х, нужно разделить обе стороны уравнения на 15 :
X = 100 / 15
X ≈ 6.6667
Таким образом, наше искомое число равно примерно 6,6667. Это быстрый способ вычисления позволяет найти ответ без применения сложных математических операций. Но важно помнить, что в реальной жизни дробные значения могут быть округлены или выражены более точно в зависимости от конкретной задачи.
Что умножить 15, чтобы получить 100 - быстрый способ вычисления

Один из самых быстрых и эффективных способов вычислить, на что нужно умножить число 15, чтобы получить 100, заключается в нахождении обратного значения этого числа и умножении его на искомое значение. В данном случае, нужно найти обратное значение для числа 15.
Обратное значение числа x представляет собой десятичную дробь, которую можно найти путем деления единицы на число x: 1/x. Таким образом, необходимо вычислить обратное значение для числа 15:
1/15 = 0.0666666667
Теперь, чтобы получить число 100, нужно умножить найденное обратное значение на 100:
0.0666666667 * 100 = 6.66666667
Таким образом, чтобы получить число 100, необходимо умножить число 15 на приблизительно 6.66666667.
Этот способ вычисления является достаточно точным и позволяет получить нужный результат без необходимости выполнять долгие вычисления в уме или использовать калькулятор.
Как узнать, на что умножить 15, чтобы получить 100?
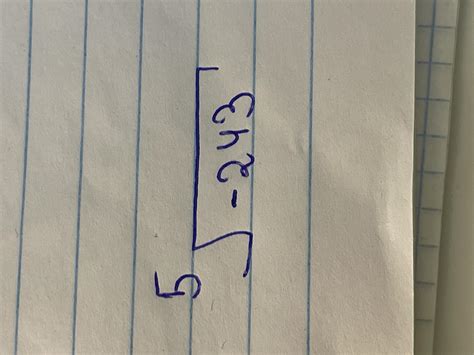
Если бы мы могли использовать десятичные числа при умножении, то ответ был бы 6.66667. Однако, в большинстве случаев требуется использовать целые числа, поэтому ответ будет 7.
Таким образом, на число 7 нужно умножить 15, чтобы получить 100.
Быстрый способ нахождения искомого числа Чтобы найти число, на которое нужно умножить 15, чтобы получить 100, можно использовать простой математический подход. Для этого нужно разделить целевое число (в данном случае, 100) на число, с которым умножается (здесь, 15). Таким образом, мы находим ответ. В данном случае: 100 / 15 = 6,666666666666667. Итак, чтобы получить 100, нужно умножить 15 на округленное до двух знаков после запятой значение 6,67. |
Умножение и деление как простые арифметические действия

Умножение - это операция, при которой одно число увеличивается в заданное количество раз. Например, если мы умножим число 5 на 3, то получим результат 15, потому что 5 × 3 = 15. Операцию умножения можно представить как сложение одного числа с самим собой несколько раз. Например, 5 × 3 можно представить как 5 + 5 + 5.
Деление - это операция, при которой одно число делится на другое число. Например, если мы разделим число 15 на 5, то получим результат 3, потому что 15 ÷ 5 = 3. Операцию деления можно представить как распределение одного числа на несколько равных групп. Например, 15 ÷ 5 можно представить как разделение 15 на 5 равных групп, где каждая группа содержит по 3 элемента.
Умножение и деление - это простые арифметические действия, которые мы часто используем в повседневной жизни. Знание этих операций помогает нам решать задачи связанные с расчетами, измерениями и многими другими ситуациями, где требуется проводить простые математические операции.
Важность знания таблицы умножения для быстрого вычисления
Знание таблицы умножения позволяет выполнять умножения в уме, без необходимости использования калькулятора или бумажного блока. Это не только экономит время, но и развивает интеллектуальные способности, улучшает концентрацию и позволяет решать задачи более эффективно.
Например, чтобы найти результат умножения 15 на 7, необходимо знать, что 7 умножить на 1 даёт 7, на 2 - 14, на 3 - 21, и так далее. С помощью знания таблицы умножения, можно сразу же определить, что 15 умножить на 7 будет равно 105.
Знание таблицы умножения также позволяет легко выполнять различные операции - деление, нахождение обратного числа и другие. Оно даже помогает в повседневной жизни, например при посещении магазина, когда нужно быстро сосчитать стоимость нескольких товаров.
Поэтому, развитие навыка знания таблицы умножения должно быть приоритетом в обучении детей. Регулярные тренировки и повторение помогут закрепить знания и сделать умножение автоматическим процессом, что значительно упростит выполнение математических операций в будущем.
Техника умножения на две цифры

Умножение на двухзначное число может показаться сложным заданием, но с правильной методикой можно выполнить его быстро и безошибочно. В данном разделе мы рассмотрим технику умножения на двух цифры.
Шаг 1: Разбиение чисел
Первый шаг заключается в разбиении обоих чисел на десятки и единицы. Например, если у нас есть число 15, мы можем представить его как 10 + 5.
Шаг 2: Умножение десятков
Затем мы умножаем десятки одного числа на число другого. Например, если у нас есть число 15 и мы хотим умножить его на 35, мы умножаем 10 на 35, что дает нам 350.
Шаг 3: Умножение единиц
После этого мы умножаем единицы одного числа на число другого. В нашем примере у нас есть 5 единиц в числе 15, и мы умножаем их на 35, получая 175.
Шаг 4: Сложение
В финальном шаге мы складываем результат умножения десятков и результат умножения единиц. В нашем примере это 350 + 175, что дает нам результат 525.
Таким образом, используя эту технику умножения на двух цифрах, мы можем быстро вычислить произведение двух чисел. Помните, что практика и привыкание к этому методу помогут сделать вычисления еще более быстрыми и точными.
Специальные числа, которые помогут найти решение

Чтобы найти число, на которое необходимо умножить 15, чтобы получить 100, можно разделить 100 на 15. На первый взгляд результат этого деления будет десятичной дробью, но на самом деле она является периодической десятичной дробью. В данном случае, результат будет представлен как 6,666... (6.666...).
Так как мы ищем целое число, на которое нужно умножить 15, мы можем округлить данное специальное число до ближайшего целого значения. В данном случае округление будет в большую сторону, поскольку 6,666... (6.666...) ближе к 7, чем к 6. Таким образом, ответ на данный вопрос будет 7.
Таким образом, специальное число 6,666... (6.666...) позволяет быстро и легко найти решение данной задачи и определить, на что умножить число 15, чтобы получить 100.
Улучшение навыка ментального вычисления

Существует множество способов развить навык ментального вычисления. Один из них - осознанное практикование. Регулярные тренировки помогут улучшить скорость и точность вычислений, а также укрепить мозговые связи, связанные с математикой. Можно начать с простых операций и постепенно переходить к более сложным.
Еще один прием для улучшения навыка ментального вычисления - использование хитростей и трюков. Некоторые числа имеют особые свойства, которые можно использовать для упрощения вычислений. Например, для умножения числа на 15 можно воспользоваться "правилом 15". Вместо того, чтобы умножать число на 15, можно умножить его сначала на 10, а затем прибавить половину самого числа. Например, чтобы умножить 24 на 15, мы сначала умножаем на 10 (240) и затем прибавляем половину числа (12), что дает нам результат 360.
Улучшение навыка ментального вычисления требует практики и терпения. Чем больше вы будете тренировать свой мозг, тем лучше станете в ментальном вычислении. Не бойтесь использовать различные хитрости и трюки, которые помогут вам сократить время и упростить сложные вычисления.



