Формула Ампера является одной из основных формул в физике, которая позволяет определить магнитное поле, возникающее вокруг проводящего электрического тока. Эта формула была открыта французским физиком Андре-Мари Ампером в начале XIX века и стала одним из важных законов электромагнетизма.
Формула Ампера устанавливает, что сила магнитного поля прямо пропорциональна силе электрического тока и обратно пропорциональна расстоянию от провода, по которому протекает ток. Таким образом, с помощью формулы Ампера можно определить интенсивность магнитного поля в любой точке пространства вблизи провода.
Формула Ампера находит много применений в современной технике и науке. Она используется для расчета магнитного поля, создаваемого электромагнитами, соленоидами, электромагнитными клапанами, а также для определения силы и плотности магнитного поля, которые могут влиять на магнитные материалы и электромагнитные устройства.
Вычисление с помощью формулы Ампера помогает инженерам и физикам разрабатывать и проектировать различные устройства, основанные на явлениях электромагнетизма, такие как электромагниты, генераторы, двигатели и трансформаторы. Формула Ампера также используется при решении задач в физических и инженерных науках, связанных со свойствами магнитных полей и влиянием электромагнитных явлений.
Роли формулы Ампера в определении физических явлений

Одной из ролей формулы Ампера в физических явлениях является определение магнитного поля вокруг проводника с током. Согласно закону Ампера, интеграл от силы магнитного поля по замкнутому контуру равен произведению тока, пронизывающего этот контур, на коэффициент пропорциональности.
Формула Ампера также используется для вычисления магнитного поля вокруг соленоида или катушки с проводником. С помощью этой формулы можно определить форму и силу магнитного поля внутри и вокруг таких устройств.
Кроме того, формула Ампера играет важную роль в определении силы взаимодействия между двумя параллельными проводниками с током. В соответствии с законом Ампера, сила взаимодействия пропорциональна произведению силы магнитного поля каждого проводника и длины сегмента проводника, через который протекает ток.
Таким образом, формула Ампера играет важную роль в определении и описании различных физических явлений, связанных с магнитным полем и током. Она позволяет рассчитывать и предсказывать взаимодействия и эффекты, связанные с этими явлениями, и находит применение в различных областях науки и техники.
Магнитное поле вокруг проводника
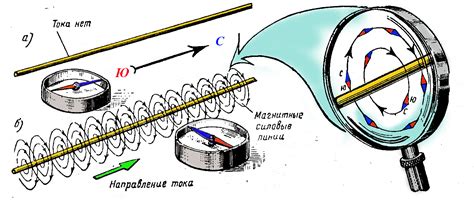
Согласно формуле Ампера, интеграл от магнитной индукции (B) по замкнутому контуру (c) равен произведению электрического тока (I) внутри контура и коэффициента пропорциональности (μ0), который называется магнитной постоянной:
| Формула Ампера: | ∮cB·dl = μ0·I |
|---|
Используя формулу Ампера, можно определить магнитное поле вокруг прямолинейного проводника, кругового проводника, спиральной катушки и других геометрических форм. Зная величину электрического тока и геометрию проводника, можно рассчитать интенсивность магнитного поля в различных точках пространства.
Магнитное поле вокруг проводника имеет особенности, такие как симметрия и силовые линии, которые формируются вокруг проводника. Также важно отметить, что направление магнитного поля зависит от направления электрического тока в проводнике. Формула Ампера позволяет учесть все эти особенности и определить магнитное поле вокруг проводника.
Формула Ампера имеет широкое применение в различных областях, включая электротехнику, электронику и физику. Это один из основных инструментов, используемых для анализа и проектирования магнитных систем и устройств. Понимание магнитного поля вокруг проводника является важным для работы с электромагнетическими явлениями и устройствами, такими как электромагнеты, соленоиды и электромагнитные клапаны.
Закон Ампера и сила электромагнитного поля

Закон Ампера, выраженный в формуле, позволяет определить силу электромагнитного поля, возникающего при прохождении тока через проводник.
Согласно закону Ампера, сила электромагнитного поля вокруг проводника пропорциональна величине тока и обратно пропорциональна расстоянию до проводника. Формула Ампера позволяет вычислить силу этого поля, используя данные о токе и расстоянии.
Формула Закона Ампера имеет вид:
F = (μ₀/2π) * (I₁ * I₂ * sinθ)/d
где:
- F - сила электромагнитного поля;
- μ₀ - магнитная постоянная, значение которой равно 4π * 10^-7 Н/А²;
- I₁, I₂ - величины токов, проходящих через проводники;
- θ - угол между направлениями этих токов;
- d - расстояние между проводниками.
Благодаря формуле Ампера, можно определить силу электромагнитного поля, что является важным величиной при решении задач и проектировании устройств, работающих на основе электромагнитных явлений.
Индукция электрического тока в круговом проводнике

С помощью формулы Ампера можно определить индукцию электрического тока в круговом проводнике. Формула Ампера связывает магнитное поле, ток и путь интегрирования. Индукция тока может быть рассчитана с использованием следующей формулы:
B = μ0 * I * l / (2 π * r)
Где B - индукция магнитного поля, μ0 - магнитная постоянная, I - сила тока, l - длина проводника, r - расстояние от центра проводника.
Эта формула позволяет определить магнитное поле, создаваемое круговым проводником при протекании через него электрического тока. Индукция электрического тока в круговом проводнике может быть использована для расчета силы, действующей на другой проводник или магнит, находящихся в этом поле.
Кроме того, формула Ампера может быть использована для определения индукции тока в других геометрических конфигурациях проводников, таких как прямолинейный проводник или соленоид. Это позволяет рассчитать магнитное поле в различных устройствах и системах.
Использование формулы Ампера в определении индукции электрического тока в круговом проводнике помогает в практических расчетах и проектировании магнитных устройств.



