Формулы являются неотъемлемой частью многих областей науки, начиная от математики и физики, и заканчивая химией и биологией. Они помогают выразить законы и закономерности природы, описать сложные процессы и взаимодействия. Формулы могут содержаться в уравнениях, функциях, теоремах, их использование позволяет производить точные расчеты и прогнозы.
Список формул, которые могут встречаться в научных и учебных материалах, весьма обширен. Он включает в себя:
- Математические формулы - такие как уравнения, функции, интегралы, дифференциалы и многое другое. Они используются для решения задач в математике, физике, экономике и других научных дисциплинах.
- Химические формулы - включают в себя соединения и реакции, представленные символами элементов и числами. Они используются для описания химических реакций и состава веществ.
- Биологические формулы - описывают ключевые процессы в биологии, такие как генетические коды, молекулярные структуры и биохимические реакции.
Важно отметить, что формулы являются универсальным языком для передачи знаний и исследований в научных областях. Они позволяют ученым и специалистам обмениваться информацией и строить дальнейшие исследования на основе уже имеющихся результатов.
Понятие формулы и ее значение

Значение формулы - это результат вычисления формулы при заданных значениях переменных. Оно может быть числом или другим математическим объектом, таким как множество или график. Значение формулы может использоваться для решения различных математических задач, моделирования реальных процессов или анализа данных.
Формулы являются важным инструментом в математике, физике, химии, экономике и других науках. Они позволяют представить сложные математические законы и связи в компактной и понятной форме. Формулы также используются для вычисления различных величин и прогнозирования результатов.
Ниже приведен список возможных элементов, которые могут содержаться в формуле:
| Математические операции | +, -, *, / |
| Возведение в степень | ^ |
| Круглые скобки | (, ) |
| Функции | sin, cos, tan, log и другие |
| Переменные | x, y, z и другие |
Это лишь некоторые примеры элементов, которые могут входить в состав формулы. Фактически, формулы могут быть очень разнообразными и сложными, в зависимости от конкретной математической задачи или модели, которую они описывают.
Основные элементы формулы
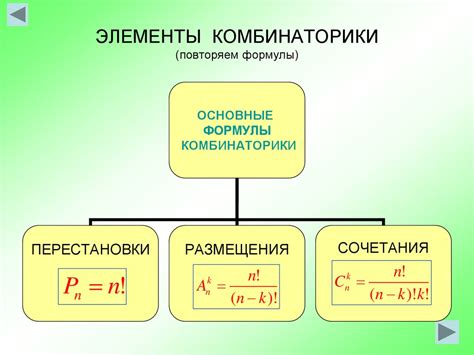
1. Числа: Формулы могут содержать числа, как константы или переменные. Числа могут быть целыми, десятичными или дробными.
2. Операции: Формулы могут содержать различные математические операции, такие как сложение, вычитание, умножение и деление. Операции выполняются между числами и переменными, чтобы получить результат.
3. Переменные: Формулы могут содержать переменные, которые представляют неизвестные значения. Переменные обычно обозначаются буквами и могут быть использованы для решения уравнений или задач, связанных с неизвестными значениями.
4. Функции: Формулы могут содержать математические функции, которые принимают один или несколько аргументов и возвращают результат. Некоторые примеры функций включают синус, косинус, экспоненту и логарифм.
Пример: Формула для вычисления площади круга (S) радиусом (r) использует переменную и математическую операцию:
S = π * r2
В этом примере "S" и "r" - переменные, "*" - операция умножения, и "π" - математическая константа, представляющая отношение длины окружности к диаметру.
Список символов, используемых в формулах
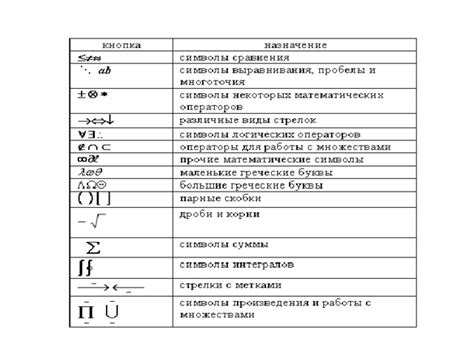
В формулах математической нотации широко используется ряд символов, которые имеют свои специфические значения и назначения. Вот некоторые из них:
- Символы операций:
- +
- -
- *
- /
- =
- <
- >
- Символы скобок:
- () - круглые скобки
- [] - квадратные скобки
- { } - фигурные скобки
- Символы индексации и верхнего и нижнего индекса:
- n - нижний индекс
- n - верхний индекс
- Символы греческого алфавита:
- α - альфа
- β - бета
- γ - гамма
- δ - дельта
- ε - эпсилон
- Символы специальных функций:
- √ - квадратный корень
- ∑ - сумма
- π - пи
- σ - сигма
Это только некоторые из символов, используемых в математических формулах. Знание и понимание этих символов позволяет более точно и ясно выражать математические понятия.
Примеры конкретных формул из предложенного списка
В предложенном списке формулы могут содержать следующие элементы:
1. Базовые арифметические операции: сложение (+), вычитание (-), умножение (*), деление (/). Например, 2 + 3 = 5.
2. Возведение в степень (^). Например, 2^3 = 8.
3. Квадратный корень (√). Например, √9 = 3.
4. Тригонометрические функции: синус (sin), косинус (cos), тангенс (tan). Например, sin(30°) = 0.5.
5. Логарифмы: натуральный логарифм (ln), десятичный логарифм (log). Например, ln(e) = 1.
6. Математические константы: число пи (π), экспонента (e). Например, π ≈ 3.14159, e ≈ 2.71828.
7. Математические функции: факториал (!), модуль (|x|), округление (round). Например, 5! = 120, |-4| = 4, round(2.6) = 3.
Это лишь некоторые примеры формул, которые могут встретиться в предложенном списке. Формулы могут быть составлены из комбинации этих элементов и использоваться для решения различных математических задач.



