Когда мы работаем с числами, часто возникает задача найти множество чисел, удовлетворяющих определенным условиям. Одним из таких условий может быть кратность чисел. Например, мы можем быть заинтересованы в поиске всех двузначных чисел, которые делятся на заданное число без остатка.
Множество двузначных чисел включает в себя все числа от 10 до 99. Чтобы найти числа, кратные заданному числу, мы должны проверить каждое число из этого множества и определить, делится ли оно на заданное число без остатка.
Для выполнения такой задачи можно использовать цикл, который будет перебирать каждое число из множества двузначных чисел. Если число делится на заданное число без остатка, мы можем добавить его в новое множество чисел, удовлетворяющих условию.
Таким образом, нахождение множества двузначных чисел, кратных заданному числу, является простой задачей, которая может быть решена с помощью цикла и проверки условия кратности. Это полезный инструмент при работе с числами и может быть применен в различных областях, включая математику, программирование и статистику.
Что такое множество двузначных чисел?
Множество двузначных чисел можно представить в виде таблицы:
| 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 | 32 | 33 |
| 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 |
| 46 | 47 | 48 | 49 | 50 | 51 |
| 52 | 53 | 54 | 55 | 56 | 57 |
| 58 | 59 | 60 | 61 | 62 | 63 |
| 64 | 65 | 66 | 67 | 68 | 69 |
| 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 |
| 82 | 83 | 84 | 85 | 86 | 87 |
| 88 | 89 | 90 | 91 | 92 | 93 |
| 94 | 95 | 96 | 97 | 98 | 99 |
Множество двузначных чисел может быть использовано при решении различных задач, в том числе и задач связанных с кратными числами.
Определение двузначных чисел

Можно заметить, что количество двузначных чисел равно 90, так как первая цифра может принимать десять значений (от 1 до 9), а вторая - десять значений (от 0 до 9). Таким образом, общее количество двузначных чисел равно 10 умножить на 10, что равно 100. Однако, у нас исключается число 00, так как оно не является двузначным числом.
Двузначные числа могут быть положительными или отрицательными, целыми или десятичными. Они являются частью натуральных чисел и используются в различных областях, таких как математика, физика, экономика и многие другие. Изучение и понимание двузначных чисел играет важную роль в развитии основных навыков математики и логики.
Как определить кратность числа?
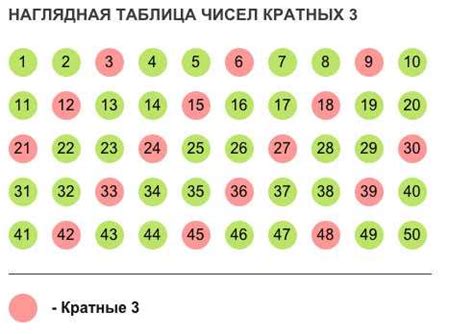
Для определения кратности числа необходимо проверить, делится ли оно на заданное число без остатка. Кратность числа означает, что число можно представить в виде произведения заданного числа на некоторое целое число.
Для этого можно использовать операцию остатка от деления (%). Если при делении числа на заданное число остаток равен нулю, то число является кратным. Например, для числа 10 и делителя 2, число 10 кратно 2, так как при делении 10 на 2 получается остаток 0.
Кратность числа может быть положительной или отрицательной. Если число делится на заданный делитель без остатка, то оно кратно этому числу. Если же при делении остается остаток, то число не кратно заданному числу.
Определение кратности числа может быть полезным при решении различных математических и арифметических задач. Например, при поиске кратных чисел для проведения деления с остатком, нахождении общих кратных чисел и т.д.
Кратность и двузначные числа

Кратность числа означает, что это число может быть делены на заданное число без остатка. В случае с двузначными числами, это значит, что в результате деления данного числа на заданное число мы получим целое число, без дробной части.
Для определения множества двузначных чисел, кратных заданному числу, можно использовать различные алгоритмы и подходы. Один из них - перебор всех двузначных чисел и проверка их кратности заданному числу.
К примеру, если заданное число равно 5, то мы можем начать перебор двузначных чисел с числа 10 и проверять каждое число на кратность 5. Если число кратно 5, то оно будет добавлено в множество двузначных чисел, кратных 5.
Используя этот алгоритм, можно быстро найти все двузначные числа, кратные заданному числу. Это может быть полезно, например, в задачах программирования или математических расчетах.
Примеры двузначных чисел, кратных заданному числу

Пример 1:
Для числа 5:
10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95
Пример 2:
Для числа 7:
14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98
Пример 3:
Для числа 12:
24, 36, 48, 60, 72, 84, 96
Это лишь некоторые примеры, и все двузначные числа, которые являются кратными выбранному числу, невозможно перечислить, так как их бесконечное множество.
Зная эти примеры, мы можем ориентироваться на понимание, что кратность представляет собой множество чисел, увеличенных на выбранное число.
Как найти все двузначные числа, кратные заданному числу?

Для того чтобы найти все двузначные числа, кратные заданному числу, нужно выполнить следующие шаги:
- Определить заданное число.
- Определить, является ли заданное число двузначным.
- Если заданное число двузначное, продолжайте шаги.
- Найти минимальное двузначное число, кратное заданному числу.
- Найти максимальное двузначное число, кратное заданному числу.
- Составить список всех двузначных чисел, кратных заданному числу, в интервале от минимального до максимального числа.
Теперь у вас есть список всех двузначных чисел, кратных заданному числу. Вы можете использовать этот список для своих нужд, например, при решении задач по программированию или математике. Удачи!



