Квадрат - это геометрическая фигура, которая имеет четыре равные стороны и четыре прямых угла. Он является одним из основных объектов изучаемых в геометрии, и знание его свойств является важным для решения множества задач.
Одним из самых простых вопросов, связанных с квадратом, является расчет значения его стороны. Если известно значение одной из сторон, то возникает вопрос о том, как найти значение оставшихся.
Формула для расчета значения стороны квадрата очень простая. Так как все стороны квадрата равны друг другу, то мы можем найти значение одной стороны, зная значение другой. Например, если сторона квадрата равна 8 см, то значение оставшихся сторон также будет равно 8 см.
Квадрат со стороной в 8 см: значение, формула и расчет
Формулой для расчета периметра квадрата с заданной стороной можно воспользоваться следующим образом:
Периметр квадрата = 4 * длина стороны
В нашем случае значение периметра будет следующим:
Периметр квадрата = 4 * 8 см = 32 см
Таким образом, периметр квадрата со стороной в 8 см составляет 32 см.
Знакомство с квадратом и его стороной

Зная длину стороны квадрата, можно определить и другие его характеристики, например, периметр (сумма длин всех сторон квадрата) и площадь (произведение длины стороны на саму себя).
Давайте рассмотрим пример. Предположим, что сторона квадрата равна 8 см. Тогда периметр данного квадрата будет равен 8 см + 8 см + 8 см + 8 см = 32 см. А его площадь будет равна 8 см * 8 см = 64 см².
Однако, чтобы рассчитать периметр и площадь квадрата, нам не обязательно знать именно длину стороны. Мы можем использовать специальную формулу для этих расчетов. Например, периметр квадрата можно рассчитать по формуле: P = 4a, где P - периметр, а - длина стороны квадрата.
В случае нашего примера: P = 4 * 8 см = 32 см.
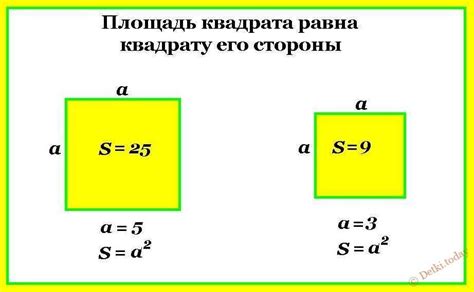
А площадь квадрата можно рассчитать по формуле: S = a^2, где S - площадь, а - длина стороны квадрата.
В случае нашего примера: S = 8 см * 8 см = 64 см².
Знание формулы и умение рассчитывать периметр и площадь квадрата по длине его стороны позволяет более гибко работать с этой геометрической фигурой и применять ее в различных задачах и вычислениях.
Важность стороны квадрата в геометрии
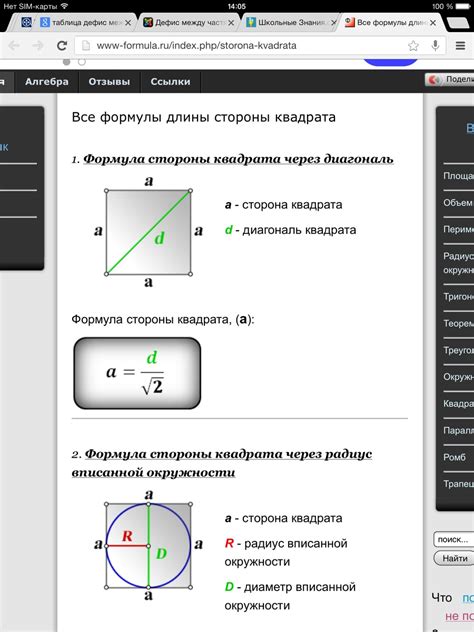
Знание стороны квадрата позволяет нам рассчитать множество других параметров, таких как периметр и площадь. Например, формула для нахождения периметра квадрата - это просто умножение длины стороны на 4.
Площадь квадрата также легко рассчитать, зная длину его стороны. Формула для нахождения площади квадрата - это квадрат длины его стороны. Таким образом, важность стороны квадрата проявляется в возможности рассчитать его основные параметры.
В геометрии сторона квадрата также играет существенную роль при решении различных задач. Например, если известна одна сторона квадрата и требуется найти другую, можно использовать теорему Пифагора или другие геометрические методы.
Таким образом, необходимо быть внимательными и не пренебрегать изучением и пониманием стороны квадрата в геометрии. Это позволит нам лучше понять основы геометрии и правильно решать задачи, связанные с квадратами и другими фигурами.
Значение стороны квадрата в математике
Значение стороны квадрата может быть различным и зависит от конкретной задачи или условий, указанных в задании.
Один из способов найти значение стороны квадрата - использовать формулу для расчета периметра квадрата. Периметр - это сумма длин всех четырех сторон квадрата.
Формула для расчета периметра квадрата: P = 4 * a, где P - периметр, a - сторона квадрата.
Если в задании указано значение периметра квадрата, то его можно использовать для нахождения значения стороны. Для этого нужно разделить периметр на 4: a = P / 4.
Например, если периметр квадрата равен 32 см, то значение его стороны будет a = 32 / 4 = 8 см.
Знание значения стороны квадрата позволяет решать различные задачи, связанные с этой геометрической фигурой, такие как нахождение площади, диагонали, и т. д.
Итак, значение стороны квадрата в математике является важным параметром, который можно найти с помощью формулы для расчета периметра квадрата или использовать, уже зная периметр. Значение стороны позволяет проводить различные вычисления и решать задачи, связанные с квадратом.
Формула для вычисления площади квадрата
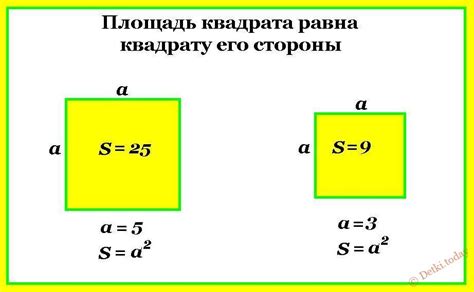
Площадь квадрата можно вычислить с помощью простой формулы. Для этого нужно умножить длину стороны квадрата на саму себя. Если сторона квадрата равна 8 см, то формула для вычисления площади будет следующей:
Площадь квадрата = сторона × сторона
Площадь квадрата = 8 см × 8 см
Подставив значения в формулу, получим:
Площадь квадрата = 64 см²
Таким образом, площадь квадрата со стороной в 8 см равна 64 см².
Использование стороны квадрата в реальной жизни
Знание длины стороны квадрата может быть полезным во многих ситуациях в реальной жизни. Например, в строительстве, можно использовать сторону квадрата для определения размеров участка земли или площади здания.
Строители часто используют квадраты для проверки прямых углов. Если все углы квадрата прямые, то можно быть уверенным в точности исполнения работ.
Также, знание стороны квадрата может помочь в расчете площадей различных поверхностей. Например, для покупки подложки или плитки для пола, можно узнать сколько квадратных метров материала понадобится.
В дизайне интерьера, сторона квадрата может использоваться для расчета размеров мебели или экспонатов. Знание размеров поможет подобрать подходящие предметы и создать гармоничный образ.
Также, зная длину стороны квадрата, можно определить его периметр и площадь, что будет полезным при изучении геометрии и математики.
В целом, знание стороны квадрата полезно во многих областях нашей жизни. Это базовое знание геометрии, которое может быть применено в повседневных ситуациях и в профессиональных областях.
Примеры расчета стороны квадрата в конкретных задачах

Представим, что у нас есть садовый участок в форме квадрата, для которого нам необходимо определить длину его стороны. В таком случае мы можем использовать формулу для расчета стороны квадрата, которая гласит: сторона = квадратный корень из площади.
Предположим, что площадь садового участка составляет 64 квадратных сантиметра. Применяя формулу, мы можем найти длину стороны следующим образом: сторона = √площадь = √64 = 8 сантиметров.
Теперь рассмотрим другую ситуацию. Допустим, у нас есть квадратный стол со стороной, измеренной в 8 сантиметров. Мы хотим узнать, какова будет площадь данного стола. В этом случае мы можем использовать формулу для расчета площади квадрата: площадь = сторона × сторона.
Применяя формулу к нашему примеру, мы найдем площадь стола следующим образом: площадь = 8 см × 8 см = 64 квадратных сантиметра.
Таким образом, применение формулы для расчета стороны и площади квадрата позволяет нам эффективно решать задачи, связанные с измерением и оценкой размеров квадратных объектов.
Способы измерения стороны квадрата
Строение квадрата подразумевает, что все его стороны равны между собой. Для определения длины стороны квадрата можно воспользоваться несколькими способами.
Первый и наиболее простой способ - использование линейки или штангенциркуля. С помощью измерительного инструмента можно точно определить длину стороны квадрата путем измерения расстояния между двумя противоположными вершинами. Результатом измерения будет значение стороны квадрата в соответствующей единице измерения, например, сантиметрах.
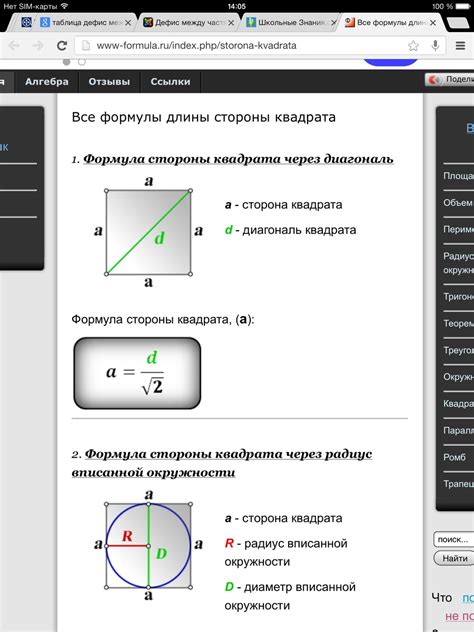
Второй способ заключается в использовании калькулятора и известной формулы для расчета стороны квадрата. Формула гласит, что длина стороны квадрата равна квадратному корню из его площади. Если известна площадь квадрата, то ее можно подставить в формулу и вычислить значение стороны.
Третий способ - использование готовых таблиц и справочников. Некоторые ресурсы предоставляют предварительно рассчитанные значения сторон квадратов с известной площадью. На таких таблицах можно легко найти нужное значение, сравнивая его с известной площадью квадрата.
Выбор способа измерения стороны квадрата зависит от наличия необходимых инструментов и первоначальных данных, однако любой из этих способов позволяет получить достоверное значение стороны квадрата.
Как узнать значение стороны квадрата без измерений
Иногда возникает необходимость узнать значение стороны квадрата, даже если нет возможности его измерить. В таких случаях можно воспользоваться различными методами расчета.
Один из простых способов – использовать площадь квадрата. Формула для вычисления площади квадрата выглядит так: S = a^2, где S – площадь, a – сторона квадрата.
Если известна площадь квадрата, то можно выразить сторону a через квадратный корень из площади. Например, если площадь квадрата равна 64 квадратным сантиметрам, то сторона будет равна квадратному корню из 64, то есть 8 сантиметрам.
Еще один способ – использовать периметр квадрата. Формула для вычисления периметра квадрата выглядит так: P = 4a, где P – периметр, a – сторона квадрата.
Если известен периметр квадрата, то можно найти значение стороны a, разделив периметр на 4. Например, если периметр квадрата равен 32 сантиметра, то сторона будет равна 32/4 = 8 сантиметрам.
Если нет возможности измерить сторону квадрата, можно воспользоваться различными математическими методами для расчета ее значения на основе известной информации, такой как площадь или периметр квадрата.
Значимость стороны квадрата для построения других геометрических фигур
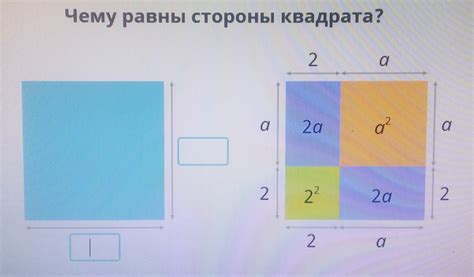
Сторона квадрата имеет большое значение в геометрии и используется для построения различных фигур. Зная длину стороны квадрата, мы можем вычислить разные параметры и размеры других форм, таких как прямоугольник, ромб, ромбоид, треугольник и т.д.
Например, если мы знаем длину стороны квадрата и хотим построить прямоугольник, мы можем использовать тот же размер стороны, чтобы определить длину и ширину прямоугольника. Это возможно, так как все углы квадрата являются прямыми углами, а значит, сторона квадрата является его диагональю.
При построении ромба, сторона квадрата может служить для определения длины его диагоналей. Каждая диагональ ромба является продолжением стороны квадрата, начинающимся из одного из его углов.
Также сторона квадрата может быть использована для определения высоты или основания треугольника. Для этого сторона квадрата может быть отложена на одной из сторон треугольника, и таким образом определить его высоту или основание.
Итак, понимание значения и характеристик стороны квадрата позволяет нам использовать ее для конструирования и анализа других геометрических фигур, обогащая наше понимание пространства и форм.



