Прямоугольник – это геометрическая фигура, у которой все углы равны 90 градусов. Он является одним из самых простых и широко распространенных многоугольников. Площадь и периметр прямоугольника можно рассчитать с помощью специальных формул.
Периметр прямоугольника – это сумма длин всех его сторон. Если длины сторон прямоугольника равны a и b, то формула для вычисления периметра будет выглядеть следующим образом: P = 2a + 2b. Например, если длина прямоугольника равна 5, а ширина – 3, то его периметр будет равен: P = 2 * 5 + 2 * 3 = 16.
Площадь прямоугольника – это произведение его двух сторон. Используя обозначения a и b для длин сторон, формула для расчета площади прямоугольника примет вид: S = ab. Например, если длина прямоугольника равна 5, а его ширина – 3, то его площадь будет равна: S = 5 * 3 = 15.
Знание формул для расчета периметра и площади прямоугольника является важным базовым навыком в геометрии. Оно позволяет решать задачи по нахождению площади земельных участков, строительства домов, а также проводить различные измерения. Поэтому помните и практикуйте эти формулы, чтобы с легкостью выполнять геометрические расчеты.
Чему равен периметр прямоугольника: формула и примеры
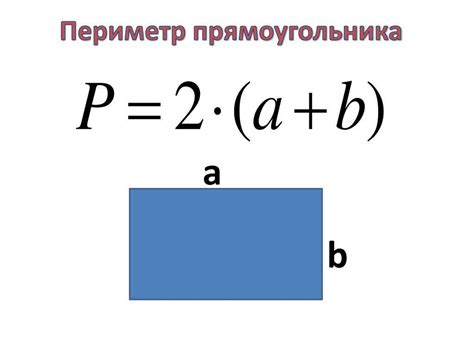
Периметр = 2 * (длина + ширина)
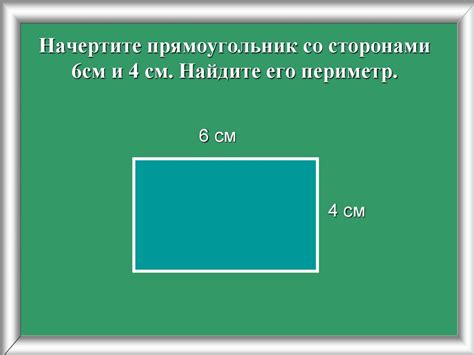
Для примера, рассмотрим прямоугольник с длиной 6 см и шириной 4 см.
Периметр этого прямоугольника равен:
Периметр = 2 * (6 см + 4 см) = 2 * 10 см = 20 см
Таким образом, периметр данного прямоугольника равен 20 см. Формула позволяет легко и быстро вычислить периметр любого прямоугольника, зная его длину и ширину.
Определение понятия "периметр прямоугольника"
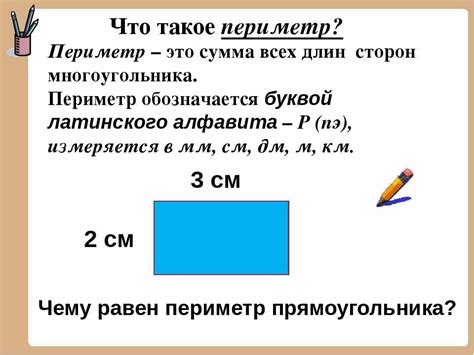
Периметр = 2a + 2b,
где a и b – длины двух сторон прямоугольника.
Например, если стороны прямоугольника равны 8 см и 12 см, то периметр будет равен:
Периметр = 2*8 + 2*12 = 16 + 24 = 40 см.
Таким образом, периметр прямоугольника равен 40 см.
Формула расчета периметра прямоугольника
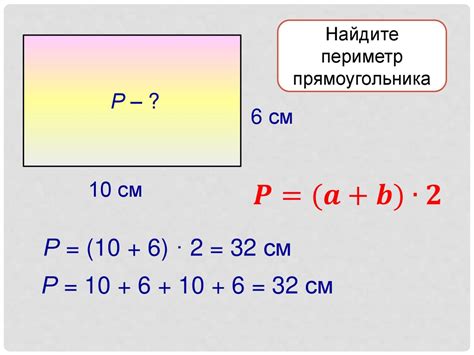
Формула для расчета периметра прямоугольника выглядит следующим образом:
P = 2a + 2b
где P - периметр прямоугольника, a - длина прямоугольника и b - ширина прямоугольника.
Например, если длина прямоугольника равна 5 см, а ширина - 3 см, то рассчитать его периметр можно по формуле:
P = 2 * 5 + 2 * 3 = 10 + 6 = 16 см
Таким образом, периметр данного прямоугольника составляет 16 см.
Примеры расчета периметра прямоугольника
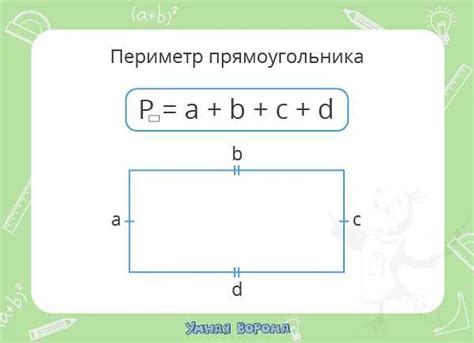
Периметр прямоугольника вычисляется по формуле:
Периметр = 2 * (длина + ширина)
Рассмотрим несколько примеров для наглядности:
Пример 1:
Дан прямоугольник со сторонами длиной 5 см и шириной 3 см. Чтобы найти его периметр, нужно использовать формулу:
Периметр = 2 * (5 + 3) = 2 * 8 = 16 см
Пример 2:
Пусть у нас есть прямоугольник с длиной 12 м и шириной 7 м. Можно вычислить его периметр следующим образом:
Периметр = 2 * (12 + 7) = 2 * 19 = 38 м
Пример 3:
Рассмотрим прямоугольник с длиной 9 дм и шириной 4 дм. Периметр можно найти так:
Периметр = 2 * (9 + 4) = 2 * 13 = 26 дм
Таким образом, зная длину и ширину прямоугольника, можно легко рассчитать его периметр, используя соответствующую формулу.
Формула расчета площади прямоугольника
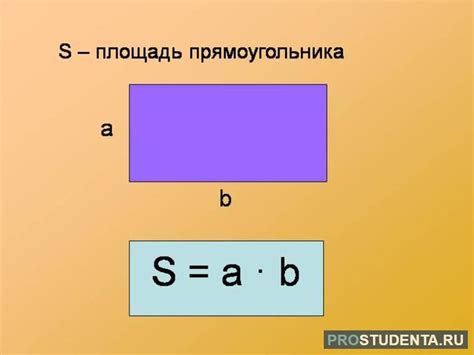
Площадь прямоугольника вычисляется как произведение его длины на ширину. Формула для расчета площади прямоугольника выглядит следующим образом:
Площадь = длина x ширина
Длина и ширина прямоугольника должны быть выражены в одной и той же единице измерения, например, сантиметры или метры. Если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь будет равна 50 квадратных сантиметров.
Формула для расчета площади прямоугольника является основной составляющей в задачах геометрии и строительства, где необходимо определить площадь поверхности для планирования материалов или вычисления затрат.
Определение площади прямоугольника с помощью формулы является довольно простым и позволяет быстро и точно рассчитать необходимые значения.
Как рассчитать площадь прямоугольника: примеры

Площадь прямоугольника можно рассчитать по формуле: площадь = длина * ширина.
Вот несколько примеров, чтобы лучше понять, как это работает:
Пример 1:
Дан прямоугольник со сторонами длиной 5 см и шириной 3 см.
Площадь прямоугольника равна 5 см * 3 см = 15 квадратных см.
Пример 2:
Дан прямоугольник со сторонами длиной 10 м и шириной 6 м.
Площадь прямоугольника равна 10 м * 6 м = 60 квадратных м.
Пример 3:
Дан прямоугольник со сторонами длиной 8 дм и шириной 4 дм.
Площадь прямоугольника равна 8 дм * 4 дм = 32 квадратных дм.
Таким образом, площадь прямоугольника рассчитывается путем умножения длины на ширину и измеряется в квадратных единицах (см², м², дм² и т. д.).
Отличия площади и периметра прямоугольника
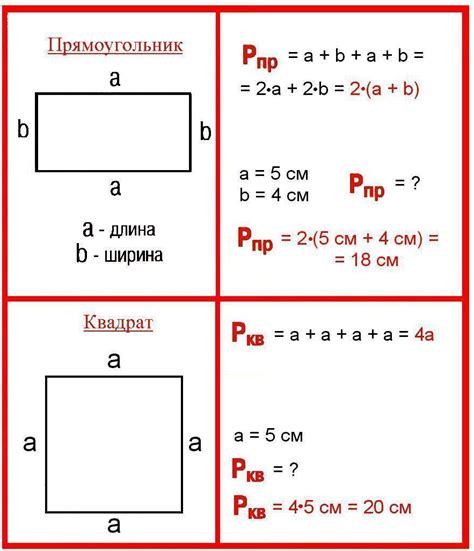
Периметр прямоугольника - это сумма всех его сторон. Для нахождения периметра нужно сложить длину всех сторон прямоугольника. Если ширина прямоугольника равна a, а длина - b, тогда периметр равен P = 2(a + b).
Площадь прямоугольника - это площадь его внутренней поверхности. Чтобы найти площадь прямоугольника, умножьте длину на ширину: S = a * b.
Таким образом, отличие между периметром и площадью прямоугольника заключается в том, что периметр - это длина границы фигуры, а площадь - это площадь внутренней поверхности. Оба понятия важны при изучении геометрии и применяются в различных практических задачах.
Значение периметра и площади прямоугольника в практических задачах
Периметр прямоугольника - сумма длин всех его сторон. Для вычисления периметра прямоугольника используется формула: P = 2a + 2b, где a и b - длины двух сторон прямоугольника.
Например, для прямоугольника со сторонами длиной 5 см и 8 см, периметр будет равен:
P = 2 * 5 + 2 * 8 = 10 + 16 = 26 см
Площадь прямоугольника - это площадь фигуры, ограниченной его сторонами. Для вычисления площади прямоугольника используется формула: S = a * b, где a и b - длины двух сторон прямоугольника.
Например, для прямоугольника со сторонами длиной 5 см и 8 см, площадь будет равна:
S = 5 * 8 = 40 см²
Знание формул для вычисления периметра и площади прямоугольника позволяет решать реальные задачи. Например, при строительстве забора нужно рассчитать необходимое количество материала, и для этого нужно знать периметр прямоугольного участка. При выборе напольного покрытия для комнаты необходимо рассчитать затраты материала, а значит, нужно знать площадь комнаты. Такие примеры можно привести множество, и понимание значений периметра и площади прямоугольника позволит эффективно решать задачи из разных областей.



