Физика - это наука, которая изучает законы природы и взаимодействие между объектами. Отличительной особенностью физики является использование математических моделей для объяснения физических явлений. Однако, для более наглядного представления и улучшения понимания физических процессов, графический подход также часто применяется.
Графическое решение задач по физике позволяет представить физические законы и явления с помощью визуальных моделей и диаграмм. Это особенно полезно при решении сложных задач, когда математические рассуждения могут быть сложными или неясными. Графический подход позволяет увидеть физическую ситуацию визуально и быстро оценить ее свойства и особенности.
При решении задач графически по физике, объекты и силы могут быть представлены в виде стрелок, диаграмм, графиков и других графических элементов. Это помогает увидеть взаимосвязи между различными переменными и силами, а также позволяет легче анализировать и понимать результаты. Графический подход также может быть использован для прогнозирования и предсказания поведения системы при изменении различных параметров.
Использование графического решения задач по физике позволяет улучшить эффективность обучения и понимания физических концепций. Визуализация физических процессов не только помогает студентам запомнить и понять теоретические основы, но и развивает их навыки анализа и критического мышления. Кроме того, графический подход позволяет студентам самостоятельно исследовать и экспериментировать, что способствует более глубокому и полному пониманию физики.
Задачи графического решения в физике
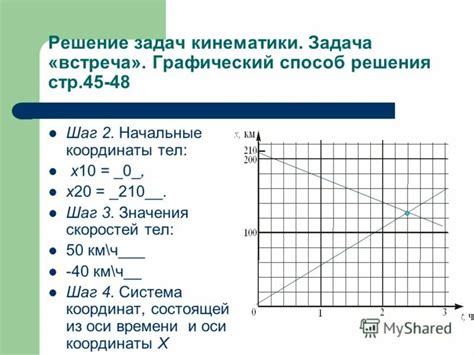
Графическое решение задач в физике имеет важное значение, так как позволяет наглядно представить различные физические явления и законы. Оно используется для визуального анализа и решения задач, а также для представления результатов экспериментов и исследований.
Одной из основных задач графического решения в физике является построение графика зависимости одной физической величины от другой. Это позволяет визуально представить связь между этими величинами и анализировать их взаимодействие. Например, график зависимости скорости от времени позволяет определить ускорение тела, а график зависимости силы от расстояния позволяет установить вид силового поля.
Графическое решение также используется для определения траектории движения объекта. Построение графика движения по известным данным о скорости и времени позволяет представить траекторию и выявить свойства движения, такие как равномерность или неравномерность.
Другим примером задач графического решения в физике является определение равновесного состояния системы. Построение графика сил, действующих на систему при различных позициях, позволяет определить точки, в которых сумма сил равна нулю. Эти точки соответствуют равновесному состоянию системы.
Также графическое решение используется для решения задач о работе и энергии. Построение графика зависимости работы или энергии от некоторого параметра позволяет анализировать изменения этих величин и связь между ними.
- Построение графиков зависимости
- Определение траектории движения
- Определение равновесного состояния системы
- Решение задач о работе и энергии
Таким образом, графическое решение задач в физике является мощным инструментом анализа и визуализации физических явлений. Оно позволяет лучше понять и исследовать законы природы, а также применять их для решения практических задач.
Изображение системы тел
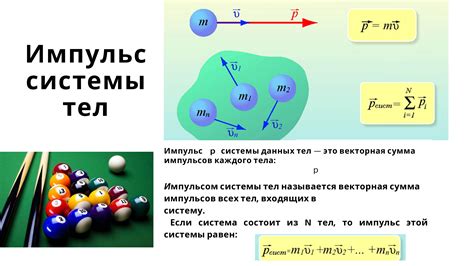
Для решения задач по физике графическим методом часто используют изображения системы тел. Такое изображение позволяет наглядно представить взаимодействие объектов и получить более полное представление о системе.
На изображении системы тел обычно обозначают каждый объект особым символом или цветом. Например, можно использовать стрелки для обозначения направления движения или векторов сил, а также разные масштабы для отображения относительных размеров объектов.
Кроме того, на изображении можно указать координатную систему, которая позволяет определить положение и перемещение объектов. Важно также учесть масштаб изображения, чтобы сохранить пропорции и относительные размеры объектов.
Изображение системы тел является важным инструментом при решении задач по физике. Оно помогает визуализировать задачу и лучше понять ее условия. Такой подход позволяет более точно определить начальные данные и связи между объектами, что в свою очередь упрощает решение задачи.
Графический метод решения задач по физике позволяет легче анализировать систему тел, пронаблюдать и оценить взаимодействие объектов в пространстве в различные моменты времени. Это особенно полезно при изучении динамики движения, колебаний и взаимодействия тел.
Анализ движения тела
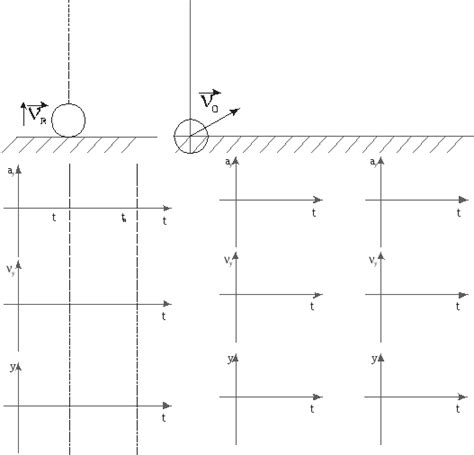
Для решения задачи графически по физике необходимо провести анализ движения тела. Анализ движения включает в себя определение начального положения тела, его скорости, ускорения, а также изменения этих параметров со временем.
Важным элементом анализа движения является построение графиков зависимости перемещения тела от времени, скорости от времени и ускорения от времени. Графики помогают наглядно представить изменение физических величин во времени и определить свойства движения тела, такие как равномерность, равнопеременность, изменение скорости и т.д.
Построение графика перемещения от времени позволяет определить, как изменяется положение тела во времени. График скорости от времени показывает, как изменяется скорость тела во времени. И, наконец, график ускорения от времени помогает понять, как изменяется ускорение тела во времени.
Используя графический метод анализа движения тела, можно определить основные характеристики движения, такие как средняя скорость, максимальная скорость, время движения, ускорение и другие параметры. Такой анализ позволяет более глубоко понять свойства движения тела и принять правильное решение по данной физической задаче.
Определение основных физических величин
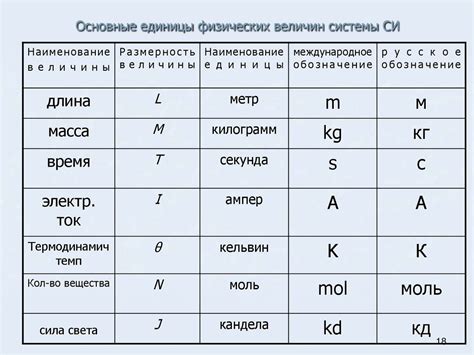
При решении задач графически по физике важно понимать основные физические величины и уметь их определять. Ниже приведена таблица с основными физическими величинами, их обозначениями и единицами измерения:
| Физическая величина | Обозначение | Единица измерения |
|---|---|---|
| Масса | m | кг |
| Длина | l | м |
| Время | t | с |
| Сила | F | Н |
| Скорость | v | м/с |
| Ускорение | a | м/с² |
| Энергия | E | Дж |
| Работа | W | Дж |
| Мощность | P | Вт |
Знание и понимание этих физических величин помогает составить правильные графики, провести нужные измерения и решить задачи графически по физике.
Исследование сил, действующих на тело
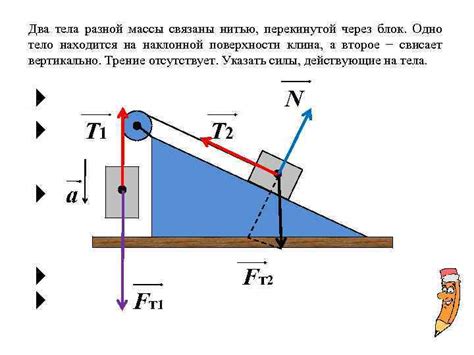
Для решения задач графически по физике необходимо провести исследование сил, действующих на тело. В первую очередь следует определить все силы, которые могут оказывать влияние на объект, а затем проанализировать их взаимодействие.
Исследование сил можно провести в несколько этапов:
- Определение гравитационной силы, действующей на объект. Гравитационная сила всегда направлена вертикально вниз и определяется по формуле F = m * g, где F - сила, m - масса объекта, g - ускорение свободного падения.
- Определение нормальной силы, которая действует перпендикулярно поверхности, на которой находится объект. Нормальная сила равна силе, которую поверхность оказывает на объект, и она равна архимедовой силе F = m * a, где m - масса объекта, a - ускорение.
- Учет сил трения. Силы трения возникают при соприкосновении двух тел и направлены в противоположную сторону относительно движения объекта. Существуют два вида сил трения: сухое трение (Fтр = μ * Fн, где μ - коэффициент трения, Fн - нормальная сила) и силы трения скольжения (Fтр = μs * Fн).
- Учет других сил. Например, если объект находится в жидкости или газе, необходимо учесть архимедову силу, действующую вверх.
После исследования всех сил можно переходить к графическому решению задачи, используя известные законы и формулы физики.
Вычисление траектории движения

Для вычисления траектории движения необходимо знать начальные условия – начальную позицию объекта и его начальную скорость. Также требуется учесть силы, действующие на объект, такие как гравитационные силы, сопротивление среды и др.
Одним из простых графических методов вычисления траектории является построение фазовых кривых. Фазовая кривая представляет собой график зависимости координаты объекта от времени. Путем последовательного построения таких кривых для различных значений начальной скорости и угла броска можно получить общую картину движения.
Другим графическим методом является векторное изображение траектории. При этом для каждого момента времени на графике строится вектор, направление и длина которого соответствуют положению объекта и его скорости соответственно. Соединив все такие векторы получится кривая, называемая векторной траекторией.
В компьютерных программных средах существуют специализированные инструменты, позволяющие вычислить траекторию движения объекта более точно и быстро. Такие программы позволяют моделировать движение объекта с учетом различных факторов и получать графическое представление о его траектории.
Решение задач с использованием графических методов

Одним из основных инструментов графического метода является использование графиков. Построение графиков позволяет наглядно увидеть зависимости между различными физическими величинами и анализировать их. На графике можно отобразить такие величины как время, скорость, ускорение, сила, перемещение и другие.
Для решения задач с использованием графических методов необходимо построить график зависимости исследуемых величин и анализировать его. По графику можно определить такие параметры, как начальные и конечные значения величин, время, длительность процесса, максимальное и минимальное значения и другие. Графический метод также позволяет сравнивать различные варианты решения задачи и выбирать оптимальный.
Графический метод в физике является удобным средством для визуализации и анализа физических процессов. Он помогает уяснить сложную материю, разобраться в зависимостях между различными величинами и принять обоснованные решения. Однако он не является единственным способом решения задач и должен быть использован вместе с другими математическими и логическими методами.
Анализ результатов и принятие решений

После выполнения задачи графически по физике и получения результатов, необходимо провести анализ полученной информации и принять соответствующие решения.
Анализ результатов может включать в себя следующие этапы:
- Изучение графиков и диаграмм. Визуализация полученных данных позволяет более наглядно увидеть тенденции и закономерности, а также выявить аномалии или неожиданные результаты.
- Интерпретация полученных значений. Определение физического смысла полученных результатов и их влияния на решение поставленной задачи.
- Сравнение с теоретическими ожиданиями. Сопоставление полученных результатов с теоретическими предположениями может помочь выявить возможные ошибки или расхождения между теорией и практикой.
- Оценка достоверности результатов. Расчёт погрешности и определение причин её возникновения позволяет оценить точность проведения эксперимента и его результатов.
На основе проведённого анализа результатов можно принять соответствующие решения:
- Внесение корректировок в процесс проведения эксперимента. Если были выявлены ошибки или несоответствия, можно модифицировать методику или провести дополнительные исследования для получения более точных результатов.
- Подтверждение или опровержение гипотезы. Если результаты эксперимента соответствуют предполагаемым значениям, это может подтвердить гипотезу и использование заданной модели. В противном случае, необходимо пересмотреть и пересчитать данные для поиска новых объяснений или моделей.
- Принятие решений на основе полученных результатов. Результаты эксперимента могут служить основой для принятия решений в различных областях, начиная от научных исследований и заканчивая разработкой новых технологий.
Важным этапом в анализе результатов и принятии решений является документирование всех проведенных действий, чтобы иметь возможность вернуться к этим данным в будущем и провести дополнительный анализ или повторить эксперимент при необходимости.



