Когда мы говорим о точках и плоскостях, мы попадаем в увлекательный мир геометрии. В геометрии каждая точка имеет свои координаты, которые определяют ее положение в пространстве. Плоскость, с другой стороны, представляет собой плоскую поверхность, состоящую из бесконечного числа точек.
Теперь представьте себе ситуацию, когда у вас есть точка и плоскость, и вам нужно доказать, что эта точка не принадлежит плоскости. Как это сделать? Существует несколько способов, и в этой статье мы рассмотрим их.
Понятие и свойства точки
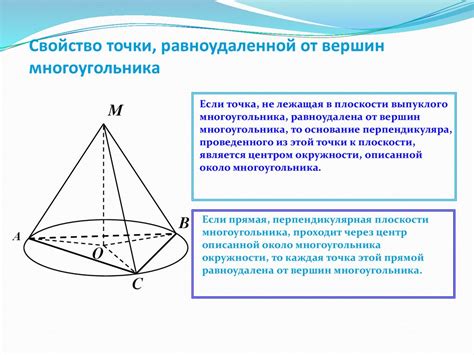
Свойства точки:
- Точка не имеет длины, ширины или высоты, она представляет только позицию в пространстве;
- Две разные точки всегда различны, каждая точка имеет свои координаты и определяет уникальное положение;
- Точка не может быть разделена, она не имеет внутренних или внешних частей;
- Точка не имеет ни ориентации, ни направления;
- Точка может быть определена в трехмерном пространстве с помощью трех координат - x, y и z, которые обычно выражают расстояния до осей координат.
Понимание понятия точки и ее свойств является основой для изучения других геометрических объектов и их взаимодействия.
Точка как элементарное понятие

Каждая точка на плоскости может быть определена парой чисел - координатами (x, y). Оси координат пересекаются в точке, называемой началом координат, которая имеет координаты (0, 0). Плоскость может быть представлена как множество всех точек, образованных парами координат.
Чтобы доказать, что точка не принадлежит плоскости, необходимо проверить, удовлетворяют ли координаты точки уравнению плоскости. Уравнение плоскости обычно задается в виде Ax + By + C = 0, где A, B и C - это коэффициенты плоскости.
Свойства точки в геометрии
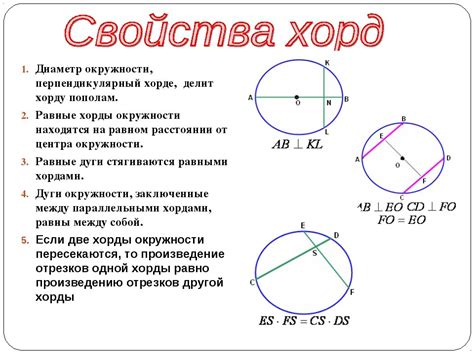
В геометрии точка обладает следующими свойствами:
| Свойство | Описание |
| Расположение | Точка может находиться в пространстве или на поверхности других геометрических объектов, таких как плоскость, окружность или прямая. |
| Безразмерность | Точка не имеет измеримых размеров, она не имеет ни длины, ни ширины, ни высоты. |
| Идентификация | Точка идентифицируется с помощью названия или символа. Например, точка A или точка P. |
| Координаты | Точка может быть определена с помощью координат. В трехмерном пространстве точка определяется тремя координатами (x, y, z). |
Используя свойства точек, геометрия позволяет анализировать и определять положение и отношения объектов в пространстве. Точка является основным строительным элементом для построения более сложных фигур, таких как линии, плоскости и многогранники.
Плоскость и ее характеристики

У плоскости есть несколько важных характеристик:
Равенство. Понятие плоскости предполагает, что все точки на этой поверхности находятся на одинаковом расстоянии от нее и располагаются на одной прямой.
Бесконечность. Плоскость не имеет начала и конца, она простирается во все стороны, что отличает ее от линии и отрезка.
Двумерность. Плоскость считается двумерным объектом, так как все ее точки описываются двумя координатами (x и y) на координатной плоскости.
Параллельность. Плоскость может быть параллельна другой плоскости, если они никогда не пересекаются.
Наклонность. Плоскость может быть наклонной, если для двух параллельных прямых, лежащих на плоскости, вертикальные проекции не равны.
Понимание характеристик плоскости поможет лучше понять ее геометрические свойства и правила, которые могут быть использованы для демонстрации того, что точка не принадлежит плоскости.
Теория плоскости
Плоскость определяется тремя нетождественными точками или двумя параллельными прямыми. Любая точка на плоскости может быть точно определена с помощью двух координат: x и y. Плоскость также может быть представлена с помощью уравнения, которое идентифицирует все точки, лежащие на этой плоскости.
Для того чтобы доказать, что точка не принадлежит плоскости, необходимо проверить выполнение уравнения плоскости для данной точки. Если уравнение НЕ выполняется, то можно утверждать, что данная точка не принадлежит плоскости.
Пример:
Дана плоскость с уравнением 2x + 3y - z = 4 и точка A(1, 2, 3). Чтобы доказать, что точка A не принадлежит плоскости, подставим координаты точки A в уравнение плоскости:
2 * 1 + 3 * 2 - 3 = 4
2 + 6 - 3 = 4
5 - 3 = 4
2 ≠ 4
Геометрические свойства плоскости

Важным свойством плоскости является то, что она является плоской, то есть все ее точки лежат в одной плоскости и не имеют третьего измерения – высоты. Также плоскость является двумерной, то есть имеет только две измеримые стороны – длину и ширину.
Плоскость обладает рядом характеристик и свойств, которые помогают ее описать и изучать. Некоторые из этих свойств включают:
| Нормаль | Плоскость имеет направление, которое перпендикулярно к плоскости и называется нормалью. Нормаль указывает направление, в котором плоскость вытянута в пространстве. |
| Угол | Плоскость может образовывать угол с другими плоскостями. Угол между двумя плоскостями определяется как угол между их нормалями. |
| Пересечение | Плоскость может пересекаться с другими плоскостями, линиями или точками. От пересечения плоскостей зависит их взаимное положение и взаимодействие. |
| Расстояние | Между двумя плоскостями можно измерить расстояние. Оно определяется как расстояние между двумя параллельными плоскостями. |
Все эти свойства позволяют изучать плоскости и использовать их в различных геометрических задачах. Например, с помощью нормали можно определить принадлежит ли точка плоскости или нет, по углу между плоскостями можно определить их взаимное положение, а расстояние между плоскостями помогает решить задачи на нахождение расстояния между двумя объектами.
Непринадлежность точки плоскости
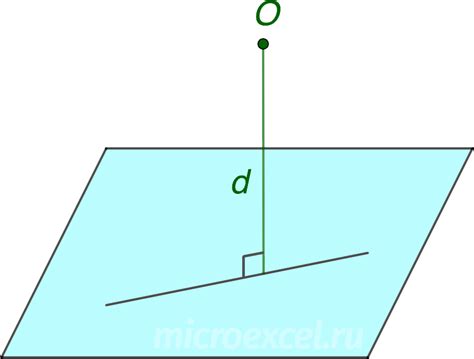
Для того чтобы доказать, что точка не принадлежит плоскости, необходимо проверить выполнение определенного условия.
Плоскость в пространстве задается уравнением вида Ax + By + Cz + D = 0, где A, B, C и D - константы, а x, y и z - координаты переменной точки.
Для проверки непринадлежности точки плоскости можно подставить значения координат этой точки в уравнение плоскости. Если после подстановки уравнение не будет выполняться, то точка не принадлежит плоскости.
Иными словами, если после подстановки координат x, y и z в уравнение плоскости, выражение Ax + By + Cz + D будет не равно нулю, то точка не лежит на плоскости.
Способы доказательства

Доказывать, что точка не принадлежит плоскости, можно использовав несколько способов. Рассмотрим некоторые из них:
1. Геометрический метод:
Способ основан на свойствах геометрических фигур и плоскостей. Необходимо проверить выполнение определенных условий, чтобы определить, находится ли точка внутри или вне плоскости.
2. Аналитический метод:
3. Проверка по свойствам плоскости:
Способ основан на свойствах плоскостей, таких как параллельность, перпендикулярность и расстояние между точками. Если точка не удовлетворяет данным свойствам, то она не принадлежит плоскости.
Выбор способа доказательства зависит от конкретной задачи и доступных данных. Важно внимательно проанализировать условия и выбрать наиболее подходящий способ доказательства.
Метод координат
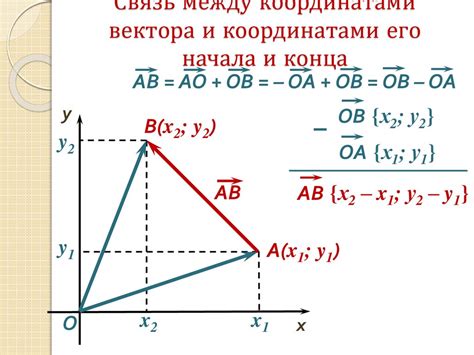
Для доказательства того, что точка не принадлежит плоскости, можно использовать метод координат.
Плоскость может быть задана уравнением вида Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты плоскости.
Чтобы проверить, принадлежит ли точка данной плоскости, необходимо подставить ее координаты в уравнение плоскости и выполнить вычисления. Если полученное выражение равно нулю, то точка принадлежит плоскости, в противном случае - точка не принадлежит плоскости.
Например, пусть есть плоскость с уравнением x - 2y + 3z - 4 = 0 и точка с координатами (1, 2, 3). Подставляя координаты в уравнение плоскости, получаем:
(1) - 2(2) + 3(3) - 4 = 1 - 4 + 9 - 4 = 2 ≠ 0
Таким образом, точка (1, 2, 3) не принадлежит плоскости.
Метод координат является одним из способов доказательства, что точка не принадлежит плоскости и может быть использован при решении различных геометрических задач.
Метод площадей
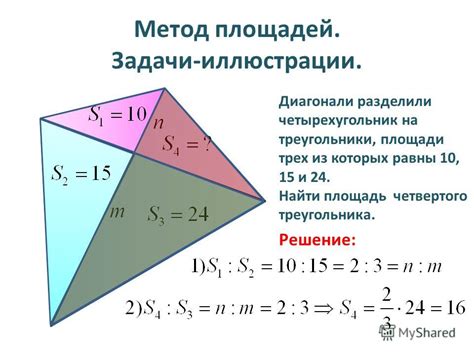
Для применения метода площадей необходимо выбрать некоторые точки на плоскости вокруг исследуемой точки. Затем строятся треугольники, образованные этими точками и исследуемой точкой. Зная координаты этих точек, можно вычислить площади образующихся треугольников.
Если площадь хотя бы одного треугольника равна нулю, то это означает, что исследуемая точка лежит на одной из сторон плоскости или совпадает с одной из вершин. Таким образом, она не принадлежит плоскости.
Если же все площади треугольников больше нуля, то это говорит о том, что исследуемая точка не лежит на одной из сторон плоскости и не совпадает ни с одной из вершин. Таким образом, можно утверждать, что точка не принадлежит плоскости.
Метод площадей является достаточно простым и эффективным способом доказательства отношений между точкой и плоскостью. Он широко используется в геометрии и математическом анализе.



