Трапеция - это геометрическая фигура, которая имеет две параллельные стороны и две непараллельные стороны, называемые боковыми сторонами. Одно из самых интересных и полезных свойств трапеции - это ее средняя линия. Средняя линия трапеции - это отрезок, соединяющий средние точки двух непараллельных сторон. Доказать, что линия действительно является средней, можно с помощью нескольких простых математических доказательств.
Первый способ доказательства средней линии трапеции основан на использовании параллелограмма. Если нарисовать параллелограмм, с одной из сторон которого является средняя линия трапеции, то можно заметить, что параллелограмм можно разбить на две равные трапеции по диагонали. Значит, средняя линия трапеции делит ее на две равные трапеции, что подтверждает ее правильность.
Второй способ доказательства средней линии трапеции использует свойства параллельных линий и пропорциональности. Если у нас есть трапеция ABCD, где AB и CD - параллельные основания, а EF - средняя линия, то можно провести линии AC и BD, которые пересекаются в точке O. Так как EF - средняя линия, то она делит соответствующие стороны трапеции на равные части. Таким образом, мы можем сказать, что отношение AO к OC равно отношению BO к OD. Из этого следует, что AC и BD делятся средней линией трапеции на две равные части, что подтверждает ее среднюю позицию.
Для лучшего понимания, рассмотрим пример. Пусть у нас есть трапеция ABCD с основаниями AB = 4 и CD = 6. Средняя линия EF равна 5. Мы можем доказать, что EF - действительно средняя линия, разделив трапецию на две равные трапеции по диагонали. Таким образом, площадь трапеции ABFE будет равна площади трапеции CDEF. Мы можем использовать формулу для площади трапеции S = (a + b) * h / 2, где a и b - длины оснований, а h - высота. Подставив значения, получим S1 = (4 + 5) * h / 2 и S2 = (5 + 6) * h / 2. Так как S1 = S2, мы можем заключить, что EF действительно является средней линией трапеции ABCD.
Средняя линия трапеции - что это и зачем она нужна
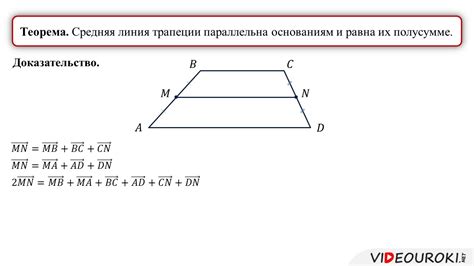
Средняя линия трапеции имеет несколько важных свойств и играет важную роль в геометрии:
- Средняя линия трапеции делит ее на две равнобедренные трапеции. Это значит, что у обеих половинок трапеции параллельные стороны равны, а углы между боковыми сторонами и основаниями равны.
- Средняя линия трапеции равна полусумме длин оснований трапеции. Для нахождения длины средней линии можно сложить длины оснований и разделить результат на 2.
- Средняя линия трапеции является осью симметрии для этой фигуры. Это означает, что при повороте трапеции вокруг средней линии на 180 градусов, она сохраняет свою форму и размеры.
- Средняя линия трапеции также используется в вычислениях и построениях. Например, она может быть использована для нахождения площади трапеции или определения положения ее вершин относительно других фигур.
Изучение средней линии трапеции помогает лучше понимать ее свойства и использовать их в практических задачах. Знание этих свойств позволяет решать задачи по геометрии более эффективно и точно.
Формула для вычисления средней линии трапеции
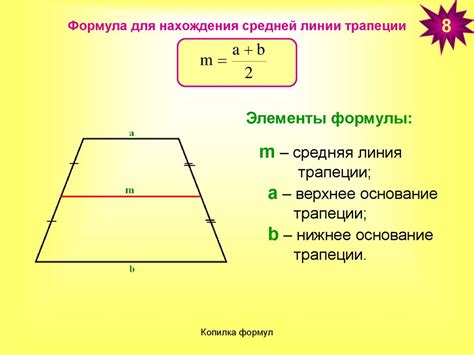
Для вычисления средней линии трапеции сначала необходимо найти сумму длин оснований и разделить ее на 2:
Медиана = (длина верхнего основания + длина нижнего основания) / 2
Например, если длина верхнего основания равна 6 см, а длина нижнего основания – 10 см, то сначала найдем их сумму: 6 + 10 = 16 см. Затем разделим полученную сумму на 2: 16 / 2 = 8 см. Полученное значение – это длина средней линии трапеции.
Формула для вычисления средней линии трапеции является одним из способов определения этого элемента геометрической фигуры. Она может использоваться при решении задач на определение различных параметров или свойств трапеции.
Пример расчета средней линии трапеции
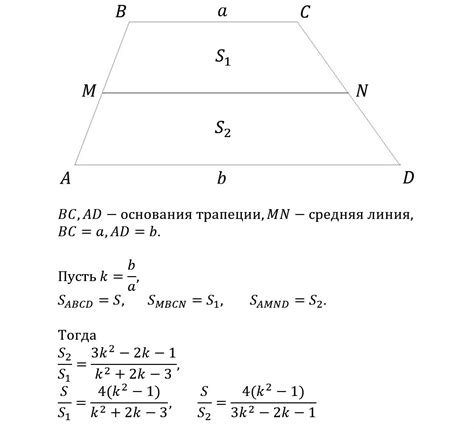
Для понимания того, как рассчитать среднюю линию трапеции, воспользуемся следующим примером. Предположим, у нас есть трапеция со следующими измерениями:
Длина основания трапеции: a = 6 см
Длина верхнего основания трапеции: b = 4 см
Высота трапеции: h = 5 см
Чтобы найти среднюю линию трапеции, сначала найдем сумму длин оснований и затем поделим полученное значение пополам:
Средняя линия трапеции = (a + b) / 2
В нашем примере:
Средняя линия трапеции = (6 + 4) / 2 = 10 / 2 = 5 см
Таким образом, средняя линия трапеции равна 5 см.
Расчет средней линии трапеции является важным шагом при работе с трапецией, так как она является основой для расчета других характеристик фигуры, например, площади или периметра.
Способы доказательства совпадения средней линии трапеции с отрезком
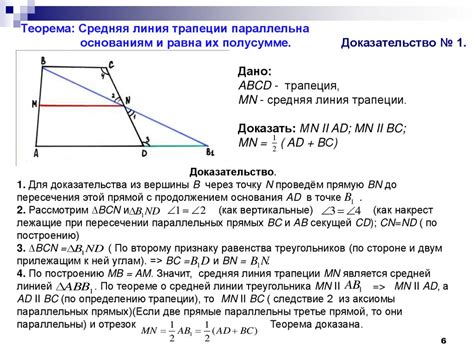
1. Метод пропорциональности сторон.
Рассмотрим треугольники, образованные средней линией и боковыми сторонами трапеции. Очевидно, что эти треугольники подобны друг другу. Следовательно, отношение длины средней линии к длине основания трапеции равно отношению длины боковой стороны к длине основания.
По определению трапеции, основания параллельны. Значит, длины оснований равны. Таким образом, получаем равенство отношений: средняя линия / основание = боковая сторона / основание.
Делим обе части равенства на основание и получаем: средняя линия = боковая сторона.
2. Метод медианы.
Используем определение медианы треугольника. Средняя линия трапеции является медианой треугольника, образованного вершиной трапеции и серединой основания. По свойству медианы, она делит основание на две равные части. Таким образом, средняя линия совпадает с отрезком, соединяющим середины оснований.
3. Метод средней линии треугольника.
Рассмотрим пару треугольников, образованных средней линией, медианой и боковой стороной трапеции. По теореме о средней линии треугольника, средняя линия параллельна и равна половине отрезка, соединяющего середины двух других сторон треугольника.
Так как боковая сторона треугольника является основанием трапеции, получаем, что средняя линия треугольника равна половине отрезка, соединяющего середины оснований трапеции. Это и означает, что средняя линия трапеции совпадает с отрезком, соединяющим середины оснований.
Применение средней линии трапеции в практике
Одно из ключевых применений средней линии трапеции заключается в вычислении площади этой фигуры. Для получения площади трапеции необходимо умножить ее среднюю линию на высоту. Таким образом, зная длину средней линии и высоту трапеции, можно легко рассчитать ее площадь.
Другое применение средней линии трапеции связано с определением ее центра тяжести. Центр тяжести трапеции находится на пересечении диагоналей, и его координаты могут быть найдены путем нахождения средних значений координат вершин трапеции. Эта информация может быть полезна для различных инженерных и архитектурных расчетов, а также для нахождения устойчивости фигуры.
Кроме того, средняя линия трапеции может быть использована для определения равнобедренности. Если длины боковых сторон трапеции равны и средняя линия является отрезком, параллельным основаниям, то трапеция является равнобедренной.



