Решение задач по сложению или вычитанию дробей требует наличия общего знаменателя. Однако в некоторых случаях общий знаменатель может быть неизвестен или его сложно найти. Что делать в таком случае?
Если нет общего знаменателя, можно воспользоваться методом преобразования дробей. Для этого нужно найти такие числа, при которых знаменатели дробей станут равными. Возможными способами являются нахождение наименьшего общего кратного или приведение дробей к эквивалентным с общим знаменателем.
Если вы не можете найти общий знаменатель, можно использовать метод приведения дробей к эквивалентным. Этот метод заключается в том, что необходимо умножить каждую дробь на такое число, чтобы их знаменатели стали равными. При этом числитель каждой дроби также умножается на это число.
Важно помнить, что после выполнения операций с дробями всегда нужно сократить их до простейших дробей. Для этого следует найти наибольший общий делитель числителя и знаменателя дроби и поделить оба числа на него.
Вычисление суммы дробей без общего знаменателя
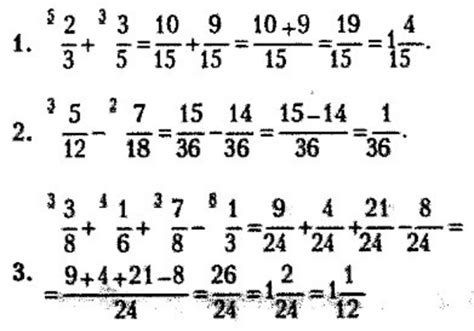
Если у вас имеется несколько дробей и нет общего знаменателя, но вам нужно вычислить их сумму, есть несколько способов сделать это.
1. Приведение дробей к общему знаменателю:
- Найдите наименьшее общее кратное (НОК) знаменателей всех дробей.
- Умножьте каждую дробь на такое число, чтобы знаменатель стал равным НОК.
- Теперь, когда все дроби имеют общий знаменатель, сложите числители и сохраните общий знаменатель.
- Если сумма дробей несократимая, упростите ее до наименьшего члена.
2. Использование десятичного представления дробей:
- Преобразуйте каждую дробь в десятичное число.
- Сложите полученные десятичные числа.
- Если сумма десятичных чисел несократимая, преобразуйте ее обратно в дробь.
Учтите, что второй способ может привести к потере точности, особенно если дроби имеют большие значения или длинные периодические числа. Поэтому, если возможно, рекомендуется использовать первый способ для вычисления суммы дробей без общего знаменателя.
Понятие общего знаменателя дробей

Как найти общий знаменатель дробей?
Для нахождения общего знаменателя дробей необходимо выполнить следующие шаги:
- Разложить знаменатели каждой дроби на простые множители.
- Взять все простые множители с наибольшей степенью, встречающиеся хотя бы в одном из знаменателей.
- Умножить эти простые множители.
Полученное произведение является общим знаменателем дробей и позволяет выполнять операции с ними.
Например, для дробей 1/3 и 1/4 общий знаменатель равен 12 (простые множители знаменателей: 3 и 2, соответственно).
Теперь, имея общий знаменатель, можно производить операции с дробями, например, сложение или вычитание.
Правила сложения дробей без общего знаменателя
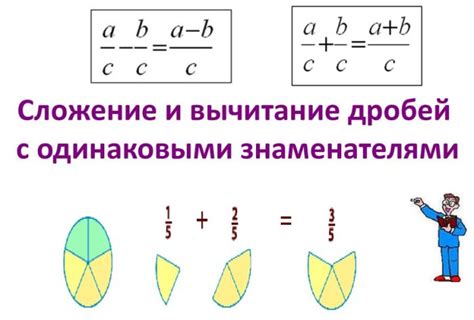
Сложение дробей без общего знаменателя может быть достаточно сложной задачей, но существуют определенные правила, которые помогут вам выполнять эту операцию правильно и эффективно.
- Первым шагом необходимо привести все дроби к общему знаменателю. Для этого найдите наименьшее общее кратное (НОК) знаменателей всех дробей и умножьте каждую дробь на такое число, чтобы ее знаменатель стал равным НОК.
- После приведения дробей к общему знаменателю сложите числители дробей и запишите результат над общим знаменателем.
- Далее упростите полученную дробь, если это возможно. Для этого найдите наибольший общий делитель (НОД) числителя и знаменателя полученной дроби и разделите оба числа на этот НОД.
Вот пример для наглядности:
- Дано: $\frac{1}{2} + \frac{1}{3} + \frac{1}{4}$
- Находим НОК знаменателей: НОК(2, 3, 4) = 12
- Приводим дроби к общему знаменателю: $\frac{1 \cdot 6}{2 \cdot 6} + \frac{1 \cdot 4}{3 \cdot 4} + \frac{1 \cdot 3}{4 \cdot 3} = \frac{6}{12} + \frac{4}{12} + \frac{3}{12}$
- Складываем числители: $\frac{6 + 4 + 3}{12} = \frac{13}{12}$
- Упрощаем полученную дробь: $\frac{13}{12} = \frac{1 \cdot 13}{3 \cdot 4} = \frac{13}{3 \cdot 4}$
Таким образом, $\frac{1}{2} + \frac{1}{3} + \frac{1}{4} = \frac{13}{12} = \frac{13}{3 \cdot 4}$.
Помните, что правила сложения дробей без общего знаменателя можно применять не только к трех дробям, но и к любому их количеству. Главное - правильно переходить от шага к шагу и не допускать ошибок при приведении дробей к общему знаменателю.
Метод приведения дробей к общему знаменателю

Основной принцип метода приведения дробей к общему знаменателю заключается в том, чтобы найти наименьшее общее кратное знаменателей данных дробей. После этого мы умножаем каждую дробь на такое число, чтобы ее знаменатель стал равным найденному общему знаменателю.
Важно отметить, что при приведении дробей к общему знаменателю необходимо также изменить числитель каждой дроби в соответствии с новым знаменателем. Как правило, числитель умножается на число, равное результату деления нового знаменателя на старый.
Например, если у нас есть дроби 3/4 и 2/5, которые нужно привести к общему знаменателю, то мы найдем наименьшее общее кратное знаменателей (в данном случае это 20) и умножим каждую дробь на такое число, чтобы ее знаменатель стал равным 20. В результате получим дроби 15/20 и 8/20.
Таким образом, метод приведения дробей к общему знаменателю позволяет нам работать с дробями, которые изначально не имеют общего знаменателя. Он является важным инструментом в алгебре и математике в целом и помогает упростить вычисления с дробями.
Взаимосвязь общего знаменателя и сложения дробей
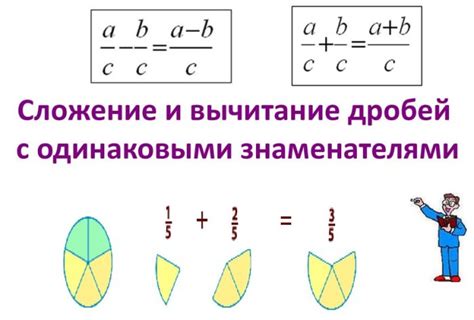
Когда у двух дробей разные знаменатели, мы не можем просто складывать числители и знаменатели отдельно. Для выполнения операции сложения необходимо привести дроби к общему знаменателю. Общий знаменатель - это наименьшее общее кратное знаменателей двух или более дробей.
Приведение дробей к общему знаменателю позволяет сравнить их, так как числители теперь будут иметь одинаковые "размеры". Это позволяет проводить операции сложения или вычитания числителей без изменения знаменателя. Например, если имеем две дроби: 1/4 и 2/5, можем привести их к общему знаменателю 20. В результате получим дроби 5/20 и 8/20, которые можно сложить, получив итоговую дробь 13/20.
Взаимосвязь общего знаменателя и сложения дробей заключается в том, что без общего знаменателя мы не сможем сравнить и объединить дроби с разными знаменателями. Общий знаменатель позволяет нам привести дроби к одному уровню и производить операции сложения и вычитания с их числителями.
Практические примеры сложения дробей без общего знаменателя

Сложение дробей без общего знаменателя может казаться сложным, но с помощью некоторых практических примеров можно это легко понять.
Предположим, у нас есть две дроби: 1/2 и 1/3. Они не имеют общего знаменателя, поэтому для сложения нужно найти общий знаменатель. В данном случае, общий знаменатель будет 6 (2 * 3 = 6).
Чтобы найти числитель новой дроби, нужно умножить числитель первой дроби на знаменатель второй и сложить с умноженным числителем второй дроби на знаменатель первой. То есть:
- Числитель новой дроби = (1 * 3) + (1 * 2) = 3 + 2 = 5
- Знаменатель новой дроби = 2 * 3 = 6
Таким образом, сумма дробей 1/2 и 1/3 равна 5/6.
Рассмотрим еще один пример: 3/4 + 1/5.
Общий знаменатель будет 20 (4 * 5 = 20).
- Числитель новой дроби = (3 * 5) + (1 * 4) = 15 + 4 = 19
- Знаменатель новой дроби = 4 * 5 = 20
Таким образом, сумма дробей 3/4 и 1/5 равна 19/20.
Эти практические примеры позволяют легче понять, как сложить дроби без общего знаменателя. Основной шаг - найти общий знаменатель, затем привести каждую дробь к этому знаменателю и сложить числители. Не забывайте сократить получившуюся дробь, если это возможно.
Способы нахождения общего знаменателя

1. Использование наименьшего общего кратного (НОК). Для нахождения общего знаменателя можно использовать НОК знаменателей данных дробей. НОК - наименьшее положительное число, которое делится на все данные числа без остатка. Найдите НОК знаменателей дробей и умножьте каждую дробь на такое число, чтобы получить общий знаменатель.
2. Использование произведения знаменателей. При отсутствии общего кратного можно использовать произведение знаменателей всех дробей в качестве общего знаменателя. Для этого перемножьте все знаменатели и умножьте каждую дробь на такое число, чтобы получить общий знаменатель.
3. Приведение дробей к эквивалентным с общим знаменателем. Если у вас есть дроби с разными знаменателями, можно привести их к эквивалентным дробям с общим знаменателем. Для этого найдите общий знаменатель, а затем приведите каждую дробь к эквивалентной дроби с этим знаменателем.
Выберите подходящий способ нахождения общего знаменателя и примените его для решения вашей конкретной задачи. Помните, что в решении задач на дроби важно сохранять равенство их значений при приведении к общему знаменателю.
Формулы для вычисления общего знаменателя

Для дробей с разными знаменателями необходимо найти их общий знаменатель перед выполнением математических операций. Существуют несколько формул для вычисления общего знаменателя:
| Формула | Применение |
|---|---|
| 1. Умножение знаменателей | Применяется, когда знаменатели имеют различные множители. Найденное произведение будет общим знаменателем дробей. |
| 2. Нахождение НОК (наименьшего общего кратного) | Применяется, когда знаменатели являются целыми числами. НОК будет являться общим знаменателем дробей. |
| 3. Приведение дробей к общему знаменателю | Применяется, когда знаменатели являются рациональными числами. Дроби приводятся к общему знаменателю путем умножения каждой дроби на составляющие общего знаменателя. |
Выбор метода зависит от конкретной ситуации и условий задачи. Часто применяется комбинация различных формул для получения наиболее удобных вычислений и минимизации ошибок.
Работа с дробями без общего знаменателя в математических задачах
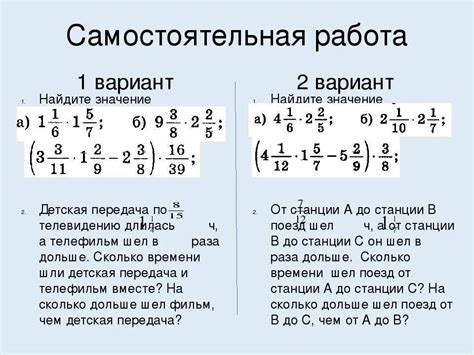
Дроби без общего знаменателя могут вызывать затруднения при решении математических задач. В таких случаях необходимо применять специальные методы, которые позволят работать с этими дробями и достичь решения задачи.
Одним из основных методов работы с дробями без общего знаменателя является приведение этих дробей к общему знаменателю. Для этого необходимо найти наименьшее общее кратное знаменателей данных дробей и умножить каждую из них на такое число, чтобы получить общий знаменатель.
После приведения дробей к общему знаменателю можно выполнить необходимые математические операции, такие как сложение, вычитание, умножение или деление.
Если задача требует простого сравнения двух дробей без общего знаменателя, можно использовать другие методы. Например, можно привести каждую из дробей к десятичному виду и сравнить полученные значения. Также возможно использование сравнения числителей дробей, если они имеют различные знаки.
При работе с дробями без общего знаменателя необходимо быть внимательным и аккуратным. Ошибки в приведении дробей к общему знаменателю или в выполнении математических операций могут привести к неверным результатам и неправильному решению задачи.
Использование таблицы для описания решаемой математической задачи с дробями без общего знаменателя может значительно облегчить процесс решения и помочь визуализировать все необходимые шаги.
| Дробь 1 | Дробь 2 | Сумма |
|---|---|---|
| a/b | c/d | (a*d + c*b) / (b*d) |
Используя эти методы и советы, можно успешно работать с дробями без общего знаменателя в математических задачах и получать правильные результаты.



