Пересечение отрезков - одна из базовых геометрических операций, которую изучают в математике уже с самых ранних классов. Эта тема важна не только для развития логического мышления учеников, но и для понимания базовых принципов геометрии. В 7 классе ученики уже достаточно знакомы с понятием отрезка и умеют работать с ними, поэтому научить их находить пересечения двух отрезков - задача совсем несложная.
Пересечение двух отрезков можно определить, используя несколько простых правил и свойств отрезков. Во-первых, необходимо определить, пересекаются ли отрезки вообще. Для этого можно воспользоваться правилом о прямоугольниках - если прямоугольники, образованные отрезками, имеют общую площадь, то отрезки пересекаются.
Если отрезки пересекаются, то необходимо определить точку пересечения. Для этого можно воспользоваться правилом о пропорциональности. Необходимо найти координаты точек отрезков и решить систему уравнений, используя формулы пропорциональности. Таким образом, можно найти точку пересечения и ответить на вопрос о пересечении отрезков в данной задаче.
Определение понятия "пересечение отрезков"
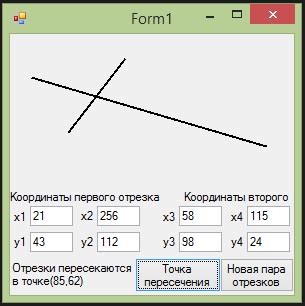
Для определения пересечения отрезков необходимо учитывать координаты начала и конца каждого отрезка. Если начало одного отрезка находится внутри другого отрезка, или конец одного отрезка находится внутри другого отрезка, то отрезки пересекаются. Если отрезки не имеют общих точек, то они не пересекаются.
Если отрезки пересекаются, то пересечение может быть представлено либо отрезком, либо точкой. Например, если один отрезок начинается внутри другого отрезка и заканчивается внутри него, то пересечение будет представлено отрезком с новыми начальными и конечными точками. Если один отрезок пересекает другой внутри, то пересечение будет представлено точкой - точкой, в которой отрезки пересекаются.
Что такое отрезок?
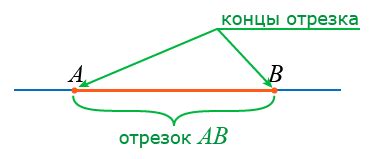
Отрезок АВ может быть описан двумя способами:
- Указать координаты точек А и В: А(х₁, у₁) и В(х₂, у₂);
- Дать две точки на прямой, которые служат концами отрезка, например, А и В.
Отрезки могут быть различной длины. Длину отрезка можно вычислить, зная координаты его концов, с помощью формулы длины отрезка:
Длина отрезка АВ = √((х₂ - х₁)² + (у₂ - у₁)²).
Отрезки могут пересекаться и не пересекаться. Если два отрезка имеют общие точки, то они пересекаются. Если отрезки не имеют общих точек, то они не пересекаются.
Что такое пересечение отрезков?
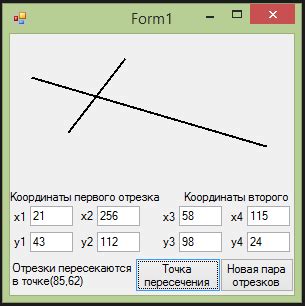
Пересечение отрезков можно представить с помощью таблицы. В таблице будут указаны координаты начальных и конечных точек каждого отрезка, а также координаты точек их пересечения, если они есть.
| Отрезок 1 | Отрезок 2 | Пересечение |
|---|---|---|
| (x1, y1) | (x3, y3) | (x, y) |
| (x2, y2) | (x4, y4) |
В ячейке таблицы, соответствующей пересечению отрезков, будут указаны координаты точки пересечения. Если точек пересечения нет, эта ячейка будет оставаться пустой.
Зная координаты начальных и конечных точек отрезков, можно сравнить их положение относительно друг друга и определить, пересекаются они или нет. Если отрезки не пересекаются, на таблице будет пустая ячейка в столбце "Пересечение".
Как определить пересечение двух отрезков?
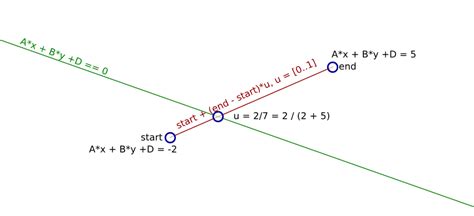
- Проверяем, лежат ли концы первого отрезка по разные стороны от отрезка CD. Если точки A и B лежат по разные стороны от прямой CD, то пересечение отрезков возможно.
- Проверяем, лежат ли точки C и D по разные стороны от прямой AB. Если точки C и D лежат по разные стороны от прямой AB, то пересечение отрезков также возможно.
- Если условия 1 и 2 выполнены, используем формулу для определения координат точки пересечения двух прямых. Для этого мы можем использовать формулы нахождения параметрического уравнения прямой и решить систему уравнений.
Если решение системы уравнений не имеет решений, то отрезки не пересекаются. В противном случае, мы можем найти точку пересечения и убедиться, что она лежит внутри обоих отрезков.
Методы определения пересечения отрезков в 7 классе
Для начала, на листе бумаги нужно нарисовать две прямые линии, которые будут представлять отрезки. Затем, с помощью линейки нужно провести вертикальные линии из концов одного отрезка к другому. Если эти вертикальные линии пересекаются, то значит отрезки имеют общую точку и пересекаются.
Еще один метод - аналитический. Он основан на использовании уравнений прямых. Для этого нужно получить уравнения прямых, заданных отрезками, и решить систему уравнений, состоящую из этих уравнений. Если система имеет решение, то отрезки пересекаются.
Также можно использовать понятие длины отрезка. Если длина одного отрезка полностью содержится внутри другого, то они не пересекаются. Если длины отрезков перекрываются хотя бы частично, то они пересекаются.
В 7 классе можно применять эти методы для определения пересечения отрезков. При желании можно также изучить более сложные методы, такие как использование углов и расчет координат точек пересечения.
Метод графического представления

Шаги для использования метода графического представления:
- Нарисуйте два отрезка на рисунке с помощью линейки и карандаша. Каждый отрезок должен иметь точку начала и точку конца.
- Обозначьте точки пересечения отрезков, если они есть. Это могут быть точки, где отрезки пересекаются, либо точки, где они касаются друг друга.
- Измерьте расстояние между точками пересечения, если они есть.
Если точки пересечения отсутствуют, значит, отрезки не пересекаются.
Метод графического представления является визуальным и позволяет наглядно представить себе ситуацию. Однако, он не всегда точен и требует определенных навыков работы с графическими представлениями. Поэтому, для более точного и надежного результата, стоит воспользоваться алгебраическими методами решения.
Метод аналитического вычисления

Чтобы найти пересечение отрезков, следует использовать систему уравнений, состоящую из уравнений прямых, на которых лежат отрезки.
- Первым шагом необходимо найти уравнения прямых, на которых лежат отрезки. Такие уравнения имеют следующий вид: y = kx + b, где k - коэффициент наклона прямой, а b - свободный член. Коэффициент наклона (k) можно найти по формуле k = (y2 - y1) / (x2 - x1), где (x1, y1) и (x2, y2) - координаты концов отрезка.
- После нахождения уравнений прямых, необходимо решить систему уравнений. Для этого необходимо приравнять значения y для обоих прямых и найти значение x. Полученное значение x подставляем в одно из уравнений прямых и находим значение y.
- Если полученные значения x и y лежат внутри отрезков, значит, отрезки пересекаются. Если же значения x и y не лежат внутри отрезков, то отрезки не пересекаются.
Метод аналитического вычисления позволяет точно определить пересечение двух отрезков по их координатам в декартовой системе координат. Однако, для его применения необходимы навыки работы с алгеброй и математическим анализом.



