Наименьшее общее кратное (НОК) двух чисел - это наименьшее число, которое делится на оба заданных числа без остатка. НОК используется в различных математических и инженерных задачах, таких как решение систем линейных уравнений, построение графиков функций и определение времени периодов колебаний.
Вычисление НОК может осуществляться различными способами, в зависимости от значений чисел. Один из наиболее простых и распространенных методов - это метод простых чисел. Сначала необходимо разложить оба числа на простые множители. Затем выбираются все простые числа, встречающиеся в разложениях с их наибольшими показателями степени. После этого перемножаются выбранные числа.
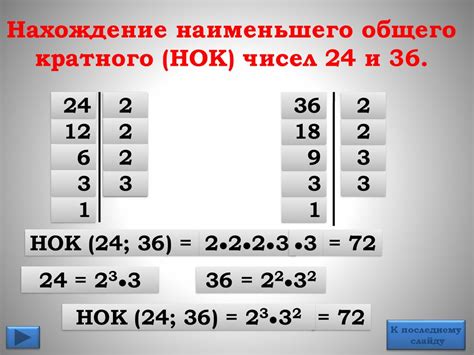
Рассмотрим пример. Пусть заданы два числа: 12 и 18. Разложим данные числа на простые множители: 12 = 2^2 * 3, 18 = 2 * 3^2. Выберем наибольшие показатели степени для каждого простого числа: 2^2 * 3^2 = 36. Таким образом, НОК чисел 12 и 18 равен 36.
Следует отметить, что в случае, если числа имеют общие простые множители, метод простых чисел не гарантирует получения НОК. В таких случаях используются другие методы, включающие нахождение максимального общего делителя (НОД) и формулу НОК = (число1 * число2) / НОД. Эти методы являются более универсальными и применимыми в любых случаях.
Что такое наименьшее общее кратное?
Основная задача при вычислении НОК заключается в определении минимального общего кратного для больших чисел или набора чисел. В этом нам помогают различные методы и алгоритмы, которые мы рассмотрим далее.
Одним из простых методов вычисления НОК двух чисел является простое перебор чисел до тех пор, пока не будет найдено число, которое делится на оба заданных числа без остатка. Однако, этот метод неэффективен для больших чисел и может занимать много времени.
Более эффективным методом вычисления НОК является использование алгоритма Евклида. Алгоритм Евклида основан на том, что наибольший общий делитель (НОД) двух чисел равен произведению чисел, поделенному на их НОК. Используя этот алгоритм, мы можем легко вычислить НОК двух чисел.
Еще одним методом вычисления НОК является расширенный алгоритм Евклида. Этот метод позволяет находить НОК не только двух чисел, но и набора чисел. Используя расширенный алгоритм Евклида, мы можем оптимизировать вычисление НОК для большого количества чисел.
Определение и основные понятия
Общие делители двух чисел — это числа, которые делятся на оба этих числа.
Наибольший общий делитель (НОД) двух чисел — это наибольшее число, которое делит оба этих числа без остатка.
Чтобы найти НОК двух чисел, можно использовать различные методы, такие как:
- Метод разложения на простые множители.
- Метод нахождения НОД через разложение на множители.
- Метод простого подсчета кратных чисел.
Методы вычисления НОК

1. Прямой подход:
- Находим кратные каждого из чисел путем умножения на последовательные числа
- Выбираем наименьшее число, которое является кратным обоим числам
2. Факторизация:
- Разлагаем оба числа на простые множители
- Находим максимальную степень каждого простого числа из разложений
- Умножаем все простые числа вместе, возведя каждое в соответствующую степень
3. Использование таблицы:
- Создаем таблицу, где столбцы - множители чисел, а строки - степени множителей
- Заполняем значениями таблицу, начиная с 0 и увеличивая значения до тех пор, пока не достигнем степеней множителей в разложениях чисел
- Вычисляем НОК, перемножая множители в каждом столбце в соответствии с их степенью
Разные методы имеют свои преимущества и недостатки, и выбор метода зависит от величины чисел и предпочтений исполнителя. При решении задач на поиск НОК, рекомендуется выбирать наиболее эффективный метод для конкретной ситуации.
Перебор делителей
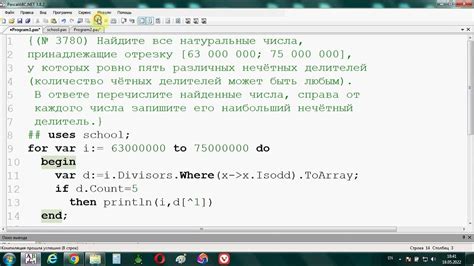
Алгоритм следующий:
- Находим все делители первого числа.
- Находим все делители второго числа.
- Находим общие делители этих чисел.
- Выбираем наименьший общий делитель.
Для перебора делителей числа используется цикл, который проходит от 1 до самого числа. Если число делится без остатка на текущий делитель, то этот делитель добавляется в список делителей данного числа.
После получения списков делителей для двух чисел, находятся их общие элементы - это будут общие делители чисел.
Выбирая наименьший общий делитель, получаем наименьшее общее кратное (НОК) двух чисел.
Формула через НОД
Наименьшее общее кратное (НОК) двух чисел можно выразить через их наибольший общий делитель (НОД) по формуле:
НОК(a, b) = (a * b) / НОД(a, b)
Данная формула основывается на том факте, что произведение двух чисел равно произведению их наименьшего общего кратного и наибольшего общего делителя.
Для вычисления НОК через НОД нужно знать значения двух чисел. Затем необходимо вычислить их НОД с помощью одного из методов (например, алгоритм Евклида) и применить формулу.
Преимущество использования формулы через НОД заключается в том, что она позволяет более эффективно вычислить НОК, не используя промежуточные значения последовательных делений.
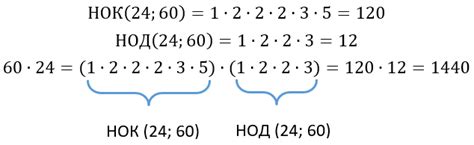
Например, для чисел 24 и 36:
НОД(24, 36) = 12
НОК(24, 36) = (24 * 36) / 12 = 72
Таким образом, НОК чисел 24 и 36 равно 72.
Разложение на простые множители

Для разложения на простые множители сначала находим наименьший простой делитель числа. Далее делим число на найденный делитель и продолжаем деление до тех пор, пока не получим неразложимое число. Затем переходим к следующему наименьшему простому делителю и продолжаем разложение до полного представления числа в виде произведения простых множителей.
Разложение на простые множители обычно представляется в виде таблицы, где в первом столбце указываются простые числа-делители, а во втором столбце указывается степень, в которую нужно возвести каждое число-делитель, чтобы получить разложение исходного числа.
| Число-делитель | Степень |
|---|---|
| 2 | 3 |
| 3 | 2 |
| 5 | 1 |
Например, разложение числа 60 на простые множители будет выглядеть следующим образом:
60 = 22 * 31 * 51
Разложение на простые множители позволяет эффективно вычислить наименьшее общее кратное двух чисел, используя формулу НОК = произведение всех уникальных простых множителей, возведенных в максимальную степень, которая присутствует в разложении каждого из чисел.
Примеры вычисления НОК

Для наглядности рассмотрим некоторые примеры вычисления наименьшего общего кратного (НОК) двух чисел:
Пример 1:
Дано два числа: 6 и 8.
Простые множители числа 6: 2, 3.
Простые множители числа 8: 2, 2, 2.
Множество всех простых множителей: {2, 2, 2, 3}.
НОК равно произведению всех простых множителей с их самой большой степенью: 23 * 3 = 24.
Пример 2:
Дано два числа: 12 и 18.
Простые множители числа 12: 2, 2, 3.
Простые множители числа 18: 2, 3, 3.
Множество всех простых множителей: {2, 2, 3, 3}.
НОК равно произведению всех простых множителей с их самой большой степенью: 22 * 32 = 36.
Пример 3:
Дано два числа: 15 и 20.
Простые множители числа 15: 3, 5.
Простые множители числа 20: 2, 2, 5.
Множество всех простых множителей: {2, 2, 3, 5}.
НОК равно произведению всех простых множителей с их самой большой степенью: 22 * 3 * 5 = 60.
Таким образом, для вычисления НОК двух чисел необходимо найти простые множители каждого числа, объединить их в множество и умножить их с их наибольшими степенями.
Пример 1

Допустим, нам необходимо найти наименьшее общее кратное (НОК) чисел 6 и 9.
Сначала составим список кратных чисел обоих чисел:
- Кратные числу 6: 6, 12, 18, 24, 30, 36, ...
- Кратные числу 9: 9, 18, 27, 36, 45, 54, ...
Мы видим, что первое общее кратное чисел 6 и 9 - это число 18.
Таким образом, НОК чисел 6 и 9 равно 18.
Пример 2

Предположим, что нужно найти наименьшее общее кратное (НОК) чисел 9 и 12.
Для начала проанализируем разложение чисел на простые множители:
| 9: | 3 * 3 |
| 12: | 2 * 2 * 3 |
Затем выберем наибольшую степень каждого множителя, представленного в разложении чисел:
| 9: | 3 * 3 | (3^2) |
| 12: | 2 * 2 * 3 | (2^2 * 3) |
И, наконец, перемножим полученные множители и получим НОК:
| НОК(9, 12) = | 2^2 * 3^2 | = 36 |
Таким образом, наименьшее общее кратное чисел 9 и 12 равно 36.
Пример 3
Допустим, мы хотим найти наименьшее общее кратное (НОК) чисел 24 и 32.
Для начала, мы можем разложить оба числа на простые множители:
| Число | Простые множители |
|---|---|
| 24 | 2, 2, 2, 3 |
| 32 | 2, 2, 2, 2, 2 |
Затем, мы можем выбрать наибольшие степени простых чисел, встречающиеся в разложении, и перемножить их:
| Простой множитель | Наибольшая степень |
|---|---|
| 2 | 3 |
| 3 | 1 |
Итак, НОК чисел 24 и 32 равно произведению наибольших степеней простых чисел:
НОК(24, 32) = 2^3 * 3^1 = 8 * 3 = 24
Таким образом, наименьшее общее кратное чисел 24 и 32 равно 24.



