Запись дробей в виде частного - это основной навык, который нужно усвоить в процессе обучения математике. Ведь дроби очень часто встречаются в нашей жизни и в различных задачах, поэтому важно знать, как правильно записывать их. В этом подробном руководстве мы рассмотрим все аспекты записи дроби в виде частного, чтобы вы могли легко справляться с любыми математическими задачами, связанными с дробями.
Дробь - это математический объект, который представляет собой число, записанное в виде частного двух чисел: числителя и знаменателя. Числитель обозначает количество одинаковых частей, которые мы рассматриваем, а знаменатель указывает на общее количество частей. Например, дробь 3/4 означает, что мы рассматриваем 3 из 4 равных частей.
Чтобы записать дробь в виде частного, мы используем дробную черту, которая разделяет числитель и знаменатель. Например, дробь 2/5 записывается как 2 пятьдесятых. Чтобы сделать запись более ясной, можно использовать круглые скобки, чтобы группировать числитель и знаменатель. Например, дробь (1+2)/3 означает, что мы складываем 1 и 2, а затем делим на 3.
Что такое дробь и частное?

Пример: дробь 3/4. Здесь числитель равен 3, что означает, что мы имеем 3 равные части, а знаменатель равен 4, что указывает, что каждая часть составляет 1/4 от целого.
Частное – это результат деления одного числа на другое. В случае с дробями, частное также будет являться дробью. Чтобы найти частное двух дробей, мы делим числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби.
Пример: частное дробей 2/3 и 2/5 равно (2/3) / (2/5). Для деления дробей, мы умножаем первую дробь на обратное значение второй дроби. Получаем следующую формулу: (2/3) * (5/2), что равно 10/6. Данная дробь может быть упрощена до 5/3.
Методы записи дробей
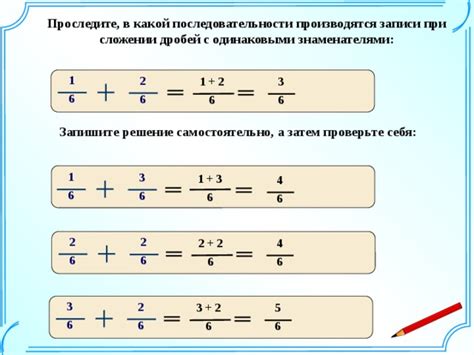
Дроби могут быть записаны в различных форматах. Ниже приведены основные методы записи дробей:
- Обыкновенная дробь: представляет собой отношение двух целых чисел, которое записывается в виде числитель / знаменатель. Например, 3/5 - обыкновенная дробь.
- Десятичная дробь: представляет собой дробь, записанную в виде десятичного числа. Например, 0.75 - десятичная дробь, которая эквивалентна обыкновенной дроби 3/4.
- Периодическая десятичная дробь: представляет собой десятичную дробь, у которой последовательность цифр повторяется в бесконечности. Например, 0.333... - периодическая десятичная дробь, которая эквивалентна обыкновенной дроби 1/3.
- Смешанная дробь: представляет собой комбинацию целой части и обыкновенной дроби. Например, 1 1/4 - смешанная дробь, которая эквивалентна обыкновенной дроби 5/4.
Запись дробей в различных форматах позволяет более точно и удобно выражать их значения и использовать в математических операциях.
Запись дроби в виде частного целых чисел

Числитель - это верхняя часть дроби, которая указывает, сколько отдельных частей целого числа имеется. Знаменатель - это нижняя часть дроби, которая указывает, на сколько частей целого числа делится каждая отдельная часть.
Процесс записи дроби в виде частного целых чисел обычно включает следующие шаги:
- Определите числитель дроби, который обозначает, сколько отдельных частей целого числа имеется.
- Определите знаменатель дроби, который обозначает, на сколько частей целого числа делится каждая отдельная часть.
- Запишите числитель и знаменатель, разделив их символом "/". Например, если числитель равен 3, а знаменатель равен 4, дробь будет записана как 3/4.
Таким образом, запись дроби в виде частного целых чисел позволяет удобно представлять и работать с рациональными числами, выражая их в виде отношения двух целых чисел.
Запись дроби в виде десятичной дроби

Для записи дроби в виде десятичной дроби необходимо выполнить следующие шаги:
- Деление числителя дроби на знаменатель
- Полученный результат представить в виде десятичной дроби
Пример:
Дана дробь 3/4.
- Делим числитель 3 на знаменатель 4: 3 ÷ 4 = 0.75
- Получаем результат в виде десятичной дроби: 0.75
Таким образом, дробь 3/4 записывается в виде десятичной дроби как 0.75.
Основные правила записи дроби в виде частного
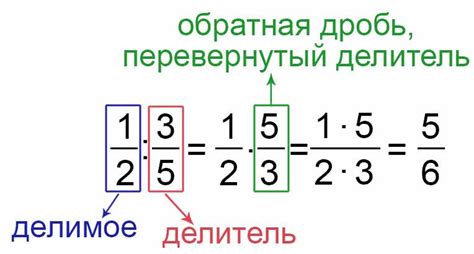
Основные правила записи дроби в виде частного включают:
| 1. | Числитель и знаменатель дроби отделяются друг от друга одноименной чертой (наклонной чертой). |
| 2. | Числитель и знаменатель дроби обычно записываются в виде целых чисел или десятичных дробей. |
| 3. | Запись дроби всегда начинается с числителя, за которым следует черта, после которой записывается знаменатель. |
| 4. | Если числитель или знаменатель состоят из нескольких цифр, они записываются без разделителей и пробелов. |
| 5. | Если числитель или знаменатель являются десятичными дробями, десятичные знаки записываются после цифр числителя или знаменателя. |
| 6. | Не сокращайте числитель и знаменатель до простейшего вида перед записью дроби в виде частного. |
| 7. | После записи дроби в виде частного, можно сократить числитель и знаменатель, если это возможно. |
Соблюдение этих основных правил позволяет корректно записывать дробь в виде частного и использовать ее в различных математических операциях.
Запись дроби с положительным числителем и знаменателем

Для записи дроби с положительным числителем и знаменателем, используются следующие шаги:
Шаг 1: Убедитесь, что числитель и знаменатель являются положительными числами. Если они отрицательные, следует сначала сделать их положительными. Например, дробь -3/5 можно преобразовать в дробь 3/5.
Шаг 2: Запишите числитель и знаменатель дроби удобным для вас способом, разделив их прямой чертой. Например, дробь 3/5 можно записать как 3/5.
Шаг 3: Округлите или сократите дробь, если это требуется. Например, дробь 6/12 можно сократить до дроби 1/2.
Пример:
Запись дроби 7/10:
Шаг 1: Числитель и знаменатель уже являются положительными числами.
Шаг 2: Запишем дробь 7/10.
Шаг 3: Данная дробь уже является сокращенной.
Таким образом, дробь 7/10 может быть записана как 7/10.
Запись дроби с отрицательными числителем и знаменателем

Для записи дроби с отрицательными числителем и знаменателем необходимо следовать определенным правилам.
1. Если только числитель отрицателен, а знаменатель положителен, то дробь записывается в виде:
-|числитель|/знаменатель
Например: -|3|/5.
2. Если только знаменатель отрицателен, а числитель положителен, то дробь записывается в виде:
|числитель|/-знаменатель
Например: |3|/-5.
3. Если и числитель, и знаменатель отрицательны, то дробь записывается в виде:
-|числитель|/-знаменатель
Например: -|3|/-5.
При записи дроби с отрицательными числителем и знаменателем необходимо помнить о расстановке знаков "-" и "/". Это поможет представить дробь в правильном виде и избежать путаницы.
Примеры записи дроби в виде частного

Вот несколько примеров, чтобы лучше понять, как записать дробь в виде частного:
Дробь 3/4 может быть записана в виде частного следующим образом:
3 ÷ 4
Дробь 5/8 можно записать в виде частного так:
5 ÷ 8
Если у нас есть дробь 7/9, то ее можно записать как:
7 ÷ 9
Дробь 2/3 будет выглядеть так:
2 ÷ 3
Дробь 9/10 может быть представлена в виде частного:
9 ÷ 10
Это лишь некоторые примеры, и дроби могут быть записаны в виде частного в зависимости от конкретного числителя и знаменателя.
Примеры записи простых дробей

1. Значение 1/2
Данная дробь представляет половину единицы. Можно записать ее в виде: 1/2.
2. Значение 3/4
Дробь 3/4 представляет три четверти единицы. Простую дробь 3/4 можно записать также как 3/4.
3. Значение 2/3
Дробь 2/3 представляет две трети единицы. Простую дробь 2/3 можно записать в виде 2/3.
Это лишь небольшой пример записи простых дробей, которые представляют собой дроби с целыми числами в числителе и знаменателе. С помощью этих примеров вы сможете легче понять принцип записи простых дробей и использовать их в решении математических задач.
Примеры записи смешанных чисел

В математике смешанное число представляет собой комбинацию целого числа и обыкновенной дроби. Запись смешанного числа обычно имеет вид целая часть + обыкновенная дробь. Например, число 3 1/2 можно записать как 3 + 1/2.
Давайте рассмотрим несколько примеров:
Пример 1: Запишем число 2 3/4.
2 3/4 = 2 + 3/4.
Пример 2: Запишем число 5 1/3.
5 1/3 = 5 + 1/3.
Пример 3: Запишем число 7 2/5.
7 2/5 = 7 + 2/5.
Это лишь несколько примеров. Смешанные числа можно записывать по-разному в зависимости от конкретной ситуации.



