Сокращение дробей является одной из основ математического анализа и является обязательным шагом при решении многих задач. В 6 классе ученики изучают основы дробных чисел и, соответственно, осваивают правила сокращения дробей.
Сокращение дроби – это процесс упрощения дроби путем сокращения ее числителя и знаменателя на их наибольший общий делитель (НОД). Сокращение дробей позволяет получить эквивалентную дробь, но с более простыми числителем и знаменателем.
Существует несколько простых способов сокращения дробей. Главное правило при сокращении дробей – делить числитель и знаменатель на одно и то же число. Для этого необходимо найти НОД числителя и знаменателя и поделить их на него.
Например, пусть дана дробь 12/18. Чтобы сократить ее, найдем НОД числителя 12 и знаменателя 18. В данном случае НОД равен 6. Делим и числитель, и знаменатель на 6 и получаем сокращенную дробь 2/3.
Знание правил сокращения дробей позволяет быстро и точно решать задачи по математике и упростить многие вычисления. Постепенно осваивая этот навык, ученики смогут более эффективно работать с дробями и успешно продолжить изучение более сложных математических тем.
Что такое сокращение дробей?
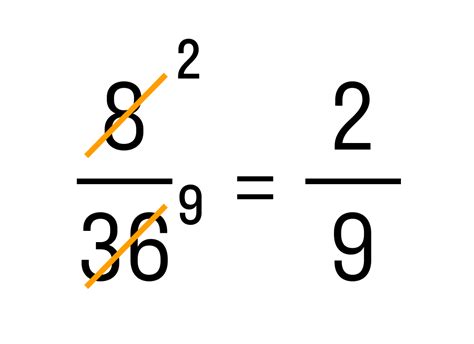
Сокращение дробей позволяет нам упростить вычисления, работу с дробями и облегчить понимание их значений. Также это помогает нам найти наибольший общий делитель числителя и знаменателя, что может быть полезно в других математических задачах.
Сокращение дробей основано на принципе равенства дроби сокращенной исходной дроби. При сокращении дроби получается такая же дробь, но числитель и знаменатель у нее меньше. Используя правила сокращения дробей, мы можем выражать дроби в более простой и удобной форме.
Сокращать дроби можно с помощью нахождения их наибольшего общего делителя (НОД). НОД - это наибольшее число, на которое делятся без остатка числитель и знаменатель дроби.
Важно отметить, что сокращение дробей не изменяет их значения. Сократив дробь, мы остаемся с той же долей от целого, но в более простой форме. Например, дробь 4/8 сокращается до 1/2, что означает, что у нас остается половина от целого, но число, которое нужно использовать для составления дроби, уменьшается.
Почему важно уметь сокращать дроби?

1. Упрощение выражений: Сокращение дробей позволяет упростить сложные выражения и сделать их более понятными. Это помогает более эффективно работать с числами и проводить алгебраические операции. | 2. Понимание отношений: Сокращение дробей помогает лучше понять отношения между числами. В результате, ученики могут лучше оценить, насколько одна дробь больше или меньше другой и сравнить их их дробные значения. |
3. Более точные ответы: Сокращение дробей позволяет получать более точные ответы при решении задач и упражнений. Когда дроби сокращаются, результаты становятся еще более точными и приближенными к истинной величине. | 4. Удобство в повседневной жизни: Умение сокращать дроби полезно в повседневной жизни. Например, при расчете скидок, разделении предметов или распределении продуктов, сокращение дробей помогает получить более удобные и понятные результаты. |
В целом, умение сокращать дроби имеет широкий спектр применений и является важным навыком, который поможет ученикам не только в школе, но и в повседневной жизни. Практиковать этот навык позволит ученикам лучше понимать и использовать математику в различных ситуациях.
Простые правила сокращения дробей
Вот некоторые простые правила, которые помогут вам сокращать дроби:
1. Ищите общие делители числителя и знаменателя.
Чтобы сократить дробь, необходимо найти все общие делители числителя и знаменателя. Общий делитель - это число, на которое можно поделить как числитель, так и знаменатель без остатка. Например, для дроби 4/8 общим делителем будет число 2, так как и 4, и 8 делятся на 2 без остатка.
2. Делите числитель и знаменатель на общий делитель.
После того, как вы нашли общий делитель, разделите числитель и знаменатель на это число. Это позволит сократить дробь до более простой и удобной формы. Например, разделив числитель и знаменатель дроби 4/8 на общий делитель 2, получим дробь 2/4, которая уже более простая и сокращена.
3. Продолжайте сокращать, если это возможно.
Иногда дробь можно сократить еще дальше, если найдется общий делитель, на который можно разделить числитель и знаменатель. Повторяйте процесс поиска и деления на общий делитель до тех пор, пока больше нельзя сократить дробь.
Например, дробь 6/9 можно сократить, разделив числитель и знаменатель на общий делитель 3. После этого получим дробь 2/3, которая уже не может быть дальше сокращена.
Знание простых правил сокращения дробей поможет вам быстро и эффективно решать задачи по математике и упрощать дроби в других областях научных и технических дисциплин.
Как найти наибольший общий делитель?
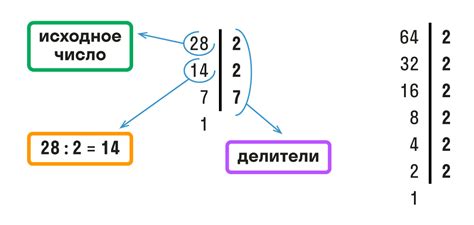
Существует несколько простых способов для вычисления НОД:
1. Метод простых чисел: Для нахождения НОД двух чисел следует разложить их на простые множители и учесть их общие множители с наименьшими показателями степени. Произведение этих общих множителей будет являться НОД.
2. Метод деления: Для нахождения НОД двух чисел можно применить алгоритм деления, известный как "алгоритм Евклида". Способ заключается в последовательном делении одного числа на другое, пока не будет получен остаток 0. НОД является последним ненулевым остатком этой последовательности делений.
3. Метод табличного поиска: Для нахождения НОД двух чисел можно составить таблицу целочисленного деления для каждого числа, начиная с 1. Затем следует найти наибольшее число, на которое оба числа делятся без остатка. Это число и будет НОД.
Зная наибольший общий делитель, можно сократить дроби, вычислить наименьшее общее кратное или произвести другие математические операции, связанные с дробями и числами.
Как сократить дробь по наибольшему общему делителю?

Чтобы сократить дробь по НОД, нужно:
- Найти НОД числителя и знаменателя дроби.
- Разделить числитель и знаменатель на найденный НОД.
Например, если у нас есть дробь 8/12, чтобы сократить ее по НОД, нужно найти НОД чисел 8 и 12. НОД(8, 12) = 4. Затем делим числитель и знаменатель на 4: 8/12 = 2/3. В итоге, дробь 8/12 сокращается до дроби 2/3.
Сокращение дробей по НОД позволяет упростить вычисления и делает задачи более понятными. Знание данного метода поможет ученикам более легко выполнять задания по сокращению дробей.
Примеры сокращения дробей

Вот некоторые примеры сокращения дробей:
- Сократить дробь 4/8:
- Числитель и знаменатель имеют общий делитель 4.
- Разделим числитель и знаменатель на 4: 4/8 ÷ 4 = 1/2.
- Упрощенная дробь: 1/2.
- Сократить дробь 12/36:
- Числитель и знаменатель имеют общий делитель 12.
- Разделим числитель и знаменатель на 12: 12/36 ÷ 12 = 1/3.
- Упрощенная дробь: 1/3.
- Сократить дробь 15/20:
- Числитель и знаменатель имеют общий делитель 5.
- Разделим числитель и знаменатель на 5: 15/20 ÷ 5 = 3/4.
- Упрощенная дробь: 3/4.
Сокращение дробей помогает упростить вычисления и работу с дробями, делая их более понятными и удобными для использования.
Полярная запись сокращенной дроби

Полярная запись сокращенной дроби представляет собой выражение, в котором числитель и знаменатель дроби имеют общий делитель, который полностью сокращается. Такая запись позволяет упростить вычисления и улучшить понимание математических операций.
Для того чтобы записать дробь в полярной форме, необходимо найти наибольший общий делитель (НОД) числителя и знаменателя. Затем числитель и знаменатель дроби делятся на этот НОД. После сокращения дроби она будет иметь наименьший возможный знаменатель и не будет содержать общих делителей.
Например, рассмотрим дробь 12/18. Найдем НОД числителя 12 и знаменателя 18. Наибольший общий делитель этих чисел равен 6. Разделим числитель и знаменатель на 6: 12/6 = 2 и 18/6 = 3. Получаем сокращенную дробь 2/3, представленную в полярной записи.
Полярная запись сокращенной дроби позволяет представить ее в наиболее простом и понятном виде. Она может быть использована для упрощения вычислений, а также для визуального представления дроби на графиках и диаграммах.



