Деление уголком - одна из основных математических операций, которая применяется во многих областях науки и жизни. Однако при делении уголком может возникнуть ситуация, когда результатом операции является десятичная дробь или нецелое число. Что же делать с остатком при делении таким образом?
В данной статье мы рассмотрим несколько практических советов по обработке остатка при делении уголком. Во-первых, можно округлить результат до ближайшего целого числа. Этот метод наиболее простой и доступный, но может не всегда быть точным. Округление можно сделать как в большую, так и в меньшую сторону, в зависимости от требуемого результата.
Во-вторых, можно выразить остаток в виде десятичной дроби и при необходимости округлить его до необходимого количества знаков после запятой. Данный метод требует некоторых знаний по работе с десятичными дробями и точностью результата. Если требуется точность до определенного числа знаков, то необходимо учесть это при округлении.
И наконец, можно оставить результат деления в виде десятичной дроби без округления. Этот метод наиболее точен, но требует работы с нецелыми числами. В некоторых случаях десятичная дробь может быть более понятной и полезной для использования, чем округленное целое число.
Практические советы: как корректно разделить остаток при делении уголком
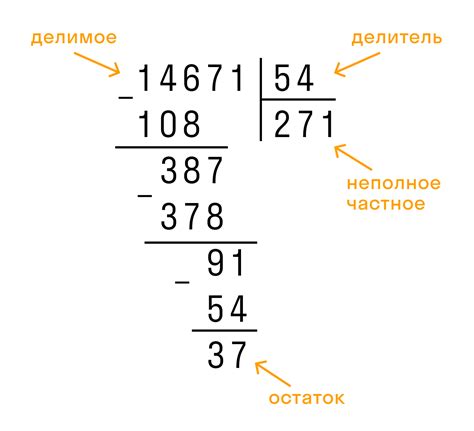
При делении одного числа на другое уголком иногда возникает остаток, который нужно правильно распределить между частями результата. В этом разделе представлены практические советы о том, как корректно разделить остаток.
1. Определите значение остатка.
Первым шагом при делении уголком является определение значения остатка. Остаток - это число, которое остается после того, как максимально возможное количество полных частей было вычтено из делимого числа. Запишите значение остатка для дальнейших вычислений.
2. Разделите остаток между долей результат и частями результата.
Вторым шагом является корректное распределение остатка между долей результата и его частями. Если остаток меньше знаменателя, добавьте его к дробной части результата. Если остаток больше или равен знаменателю, добавьте единицу к целой части результата, а остаток распределите между целой и дробной частями.
3. Установите правильный формат для результата.
Третьим и последним шагом является установка правильного формата для результата. Запишите результат в форме числитель-знаменатель, где числитель - это целая часть результат, а знаменатель - это знаменатель делителя. Если дробная часть результата равна нулю, можно не записывать ее в ответе.
Следуя этим практическим советам, вы сможете корректно разделить остаток при делении уголком и получить правильный результат.
Округление остатка

При делении с остатком важно правильно округлить полученный остаток, чтобы получить наиболее точный результат. Округление остатка зависит от требований задачи и может быть реализовано различными способами. Рассмотрим несколько практических советов:
- Если остаток при делении положительное число:
- Если остаток больше или равен половине делителя, округляем его в большую сторону.
- Если остаток меньше половины делителя, округляем его в меньшую сторону.
- Если остаток при делении отрицательное число:
- Если остаток меньше или равен минус половине делителя, округляем его в большую сторону.
- Если остаток больше минус половины делителя, округляем его в меньшую сторону.
- При округлении остатка также можно использовать различные методы округления, такие как округление до ближайшего целого числа, округление вниз или округление вверх.
Выбор метода округления остатка зависит от требований задачи и требуемой точности результата. Важно учитывать все особенности округления и выбирать наиболее подходящий метод для конкретной ситуации.
Применение целочисленного деления

Применение целочисленного деления позволяет решить ряд практических задач. Например, при работе с корзинами интернет-магазина можно использовать целочисленное деление для определения количества полных корзин, которые будут заполнены заданным количеством товара.
Также целочисленное деление может быть полезно при делении временных интервалов. Например, если задано время в секундах, то целочисленное деление на 60 позволит определить количество полных минут в данном интервале времени.
Другой пример применения целочисленного деления - разделение списка элементов на части для параллельной обработки. Целочисленное деление на количество доступных потоков позволяет определить, сколько элементов будет обработано каждым потоком, в случае, если список нельзя равномерно разделить.
| Делимое | Делитель | Результат |
|---|---|---|
| 10 | 3 | 3 |
| 20 | 7 | 2 |
| 30 | 4 | 7 |
Использование остатка при делении для дополнительных вычислений
Вот несколько практических примеров использования остатка при делении:
| Пример | Описание |
|---|---|
| 1 | Определение четности и нечетности числа. Если остаток от деления числа на 2 равен 0, то число является четным, в противном случае - нечетным. |
| 2 | Определение кратности числа другому числу. Если остаток от деления одного числа на другое равен 0, то первое число является кратным второму. |
| 3 | Разделение на группы. Если нужно разделить некоторое количество предметов на группы по определенному количеству единиц, можно использовать остаток от деления для определения количества предметов, которые останутся без группы. |
| 4 | Создание циклических паттернов. Остаток от деления может использоваться для создания паттернов или последовательностей чисел, которые повторяются с определенной периодичностью. |
Использование остатка при делении позволяет решать разнообразные задачи, связанные с обработкой чисел и определением их особенностей. Помните, что остаток может быть полезным инструментом при выполнении вычислений и помогает лучше понять свойства чисел в контексте математики.



