Полигон частот – это графическое представление результатов статистического исследования или эксперимента, проведенного для определения вероятности различных событий. В теории вероятностей полигон частот помогает наглядно представить распределение вероятностей и выявить закономерности в данных.
Основной элемент полигона частот – гистограмма, которая показывает, сколько раз каждое событие произошло в результате проведенного эксперимента. Гистограмма строится на основе столбцов, где ось X обозначает значения событий, а ось Y – количество событий, соответствующих каждой из значимых величин. Ширина столбцов гистограммы зависит от интервала, который передается на ось X.
Создание полигона частот позволяет исследователю оценить вероятностное распределение значений и определить, насколько результаты эксперимента соответствуют ожиданиям. Более того, полигон частот может помочь выявить аномалии, выбросы и асимметрии в данных, что важно для правильного анализа и интерпретации статистических результатов.
Полигон частот в теории вероятности
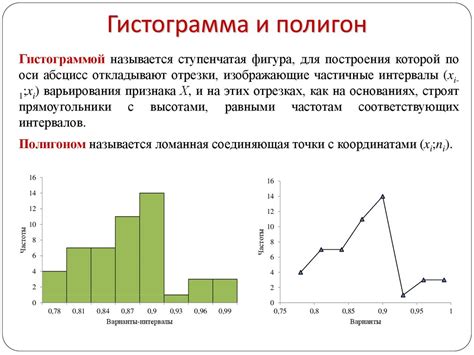
Для построения полигона частот необходимо выполнить следующие шаги:
- Собрать выборку данных
- Разделить диапазон значений на интервалы
- Подсчитать частоту появления значений в каждом интервале
- Отметить на графике точки с координатами (значение, частота)
- Провести ломаную линию через отмеченные точки
Полигон частот позволяет сравнить распределение выборки с теоретическим распределением и выявить несоответствия между ними. Кроме того, при помощи полигона можно проанализировать изменение распределения в разных группах или в разные периоды времени.
Значения на оси абсцисс полигона частот представляют собой интервалы значений. Частота появления значений в каждом интервале отображается на оси ординат. Таким образом, полигон частот позволяет визуализировать и анализировать распределение данных и определять его основные статистические характеристики, такие как среднее значение, мода и медиана.
Полигон частот является одним из основных инструментов анализа данных в теории вероятности и статистике. Он позволяет увидеть закономерности, скрытые в выборке, и провести более глубокий анализ данных. Благодаря своей наглядности и простоте использования, полигон частот широко применяется в исследованиях и анализе данных в различных областях, таких как экономика, медицина, социология и другие.
Определение и основные понятия
Основными понятиями, связанными с полигоном частот, являются:
- Значение – конкретная числовая величина, принятая в выборке.
- Частота – количество раз, которое данное значение появляется в выборке.
- Полигон частот – графическое представление распределения частот для всех значений выборки.
- Относительная частота – доля частоты, которая составляет каждое значение относительно общего числа значений выборки.
Полигон частот позволяет наглядно представить распределение значений в выборке и его вариативность. Он может быть использован для анализа данных, построения гистограммы и определения наиболее часто встречающихся значений.
История развития полигона частот
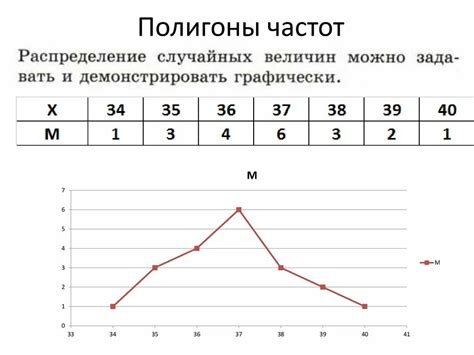
В своей работе Пирсон впервые описал алгоритм построения полигона частот, который заключается в разбиении непрерывного множественного ряда на интервалы и подсчете числа наблюдений в каждом интервале. После этого полученные значения откладываются на горизонтальной оси, а на вертикальной оси откладывается количество наблюдений в каждом интервале. Таким образом получается полигон, который позволяет визуально оценить распределение данных и выделить основные характеристики.
С течением времени полигон частот стал широко использоваться в различных областях, связанных с анализом данных. Он стал незаменимым инструментом при проведении различных исследований, а также при визуализации данных в отчетах и презентациях. В настоящее время существуют различные программы и инструменты, позволяющие автоматизировать и упростить процесс построения полигона частот.
Свойства полигона частот
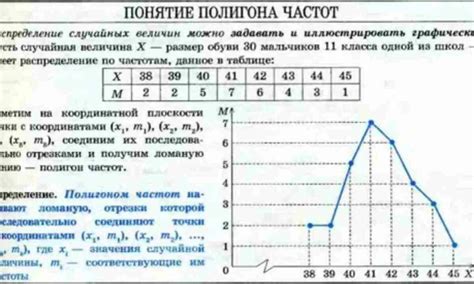
1. Наглядность: полигон частот представляет собой график, на котором по оси X откладываются значения переменной, а по оси Y откладываются частоты, с которыми эти значения встречаются в выборке. Такой наглядный график позволяет сразу увидеть, как распределены значения выборки и какие значения наиболее часто встречаются.
2. Информативность: полигон частот позволяет сделать предварительный анализ данных, выявить основные закономерности и особенности распределения переменной. Например, по полигону частот можно определить, есть ли в выборке выбросы или аномалии, какие значения наиболее типичны и какие отклоняются от среднего.
3. Сравнение: полигон частот может быть использован для сравнения нескольких выборок или наборов данных. На одном графике можно отразить несколько полигонов частот, что позволяет наглядно сравнить их распределения и выявить возможные различия или сходства.
4. Сглаживание: для улучшения визуального восприятия и интерпретации полигон частот может быть сглажен, то есть линии, соединяющие точки на графике, могут быть сглажены для создания более плавного изображения. Это особенно полезно в случае большого количества значений или при анализе непрерывных переменных.
Статистическая интерпретация полигона частот
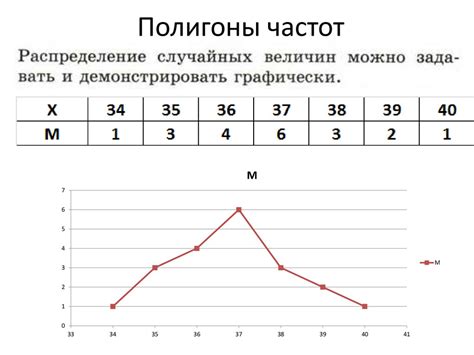
Статистическая интерпретация полигона частот позволяет наглядно представить, как часто встречается определенное значение события или переменной. Она позволяет увидеть основные характеристики данных, такие как среднее значение, разброс, асимметрия и другие.
Полигон частот становится особенно полезным при анализе качественных данных, так как позволяет визуализировать распределение частот по различным значениям переменной. В результате, исследователь может увидеть, какие значения переменной встречаются чаще, а какие реже.
Статистическая интерпретация полигона частот может также помочь выявить аномальные значения, выбросы и иные необычные особенности данных. Это позволяет более глубоко исследовать закономерности и связи между переменными.
Таким образом, полигон частот является важным инструментом в анализе данных и позволяет исследователю получить более полное представление о распределении частот и свойствах анализируемых переменных.
Отличия полигона частот от других графических методов анализа данных
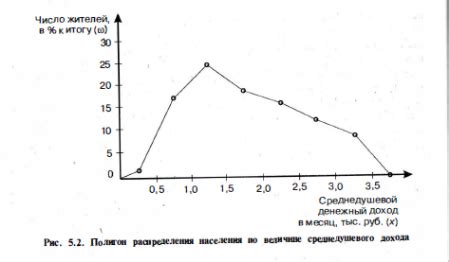
Отличие полигона частот от других графических методов анализа данных заключается в следующем:
- Другие графические методы, такие как гистограмма или круговая диаграмма, представляют данные в виде столбцов или секторов, в то время как полигон частот строится с использованием линий.
- Полигон частот позволяет более наглядно отобразить изменения в частоте, так как ломаная линия соединяет значения частот и позволяет увидеть тренды.
- Полигон частот может быть использован для сравнения нескольких распределений на одном графике, что делает его более гибким инструментом анализа данных.
- Полигон частот также может быть использован для оценки формы распределения данных, так как форма ломаной линии может указывать на наличие мод или асимметрии.
В целом, полигон частот предоставляет более детальную информацию о распределении данных, чем другие графические методы, и может быть полезным инструментом в исследовании и анализе данных.
Применение полигона частот в практических задачах
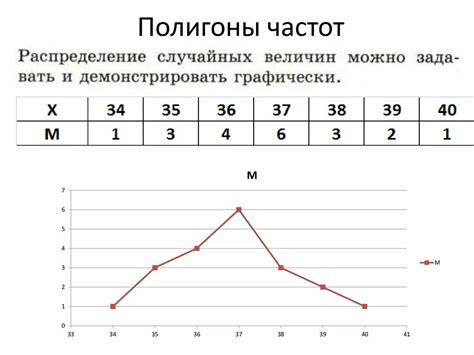
Полигон частот также может быть полезным при изучении экономических данных. Например, с помощью полигона частот можно анализировать распределение доходов населения, стоимость товаров или цены на недвижимость в определенном регионе. Это помогает бизнесам и экономистам понять, какие группы населения являются целевой аудиторией для конкретных продуктов или услуг, или определить тенденции на рынке недвижимости.
Более того, полигон частот может быть полезным средством для анализа данных о социальных проблемах. Например, он может использоваться для изучения распределения расовых или этнических групп в определенном районе, или для анализа уровня безработицы среди различных возрастных групп. Это помогает обрисовать картину социальной справедливости или неравенства и выявить проблемные области, требующие дополнительных усилий со стороны властей или общественности.
В целом, применение полигона частот в практических задачах позволяет более наглядно исследовать и анализировать данные, выявлять закономерности и тенденции, и принимать обоснованные решения на основе этих наблюдений. Этот инструмент применим во многих областях, от медицины и экономики до социальной статистики, и является важным элементом теории вероятности и статистики.
Примеры использования полигона частот
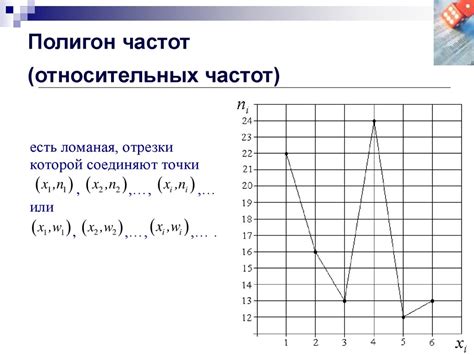
1. Статистика и социология:
Полигон частот широко используется в статистике и социологии для анализа данных и визуализации результатов исследований. Например, при изучении предпочтений людей в выборе различных продуктов, можно построить полигон частот, чтобы определить самые предпочтительные или непредпочтительные продукты.
2. Финансовая аналитика:
Полигон частот может быть использован для анализа финансовых данных, таких как распределение доходов или расходов по различным категориям. Например, если имеются данные о распределении доходов населения по возрастным группам, полигон частот позволит наглядно представить, какая группа имеет наибольший доход.
3. Маркетинг и реклама:
В маркетинге и рекламе полигон частот может быть использован для анализа данных по распределению потребителей по различным категориям или характеристикам. Например, при создании рекламной кампании можно построить полигон частот, чтобы определить характеристики целевой аудитории, такие как возраст, пол или место проживания.
Важность полигона частот в изучении вероятностных процессов
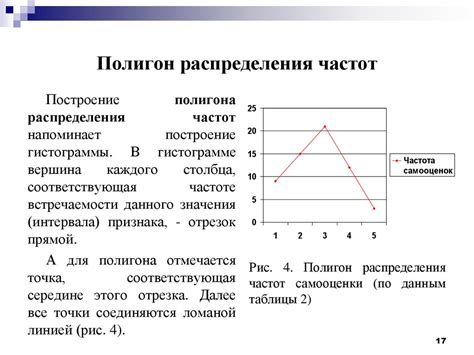
Полигон частот представляет собой графическую диаграмму, позволяющую визуально исследовать и анализировать вероятностные процессы. Он отображает относительную частоту появления определенных значений или событий.
Вероятностные процессы являются основой теории вероятностей и широко используются в различных областях, включая статистику, экономику, биологию, социологию и другие. Полигон частот позволяет получить представление о распределении вероятностей в конкретной выборке или наблюдении.
Полигон частот может быть использован для анализа больших объемов данных и выявления скрытых паттернов или зависимостей. Он помогает исследователям сформулировать гипотезы и проверить их на основе полученных результатов.
Ограничения и недостатки полигона частот
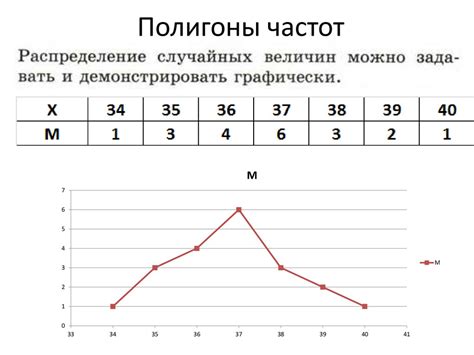
Во-первых, полигон частот может быть неудобен в случае большого числа значений или категорий. При большом количестве точек на графике становится сложно их различить и анализировать. Это особенно верно, если значения имеют маленькие отличия. В таких случаях более удобно использовать гистограмму или другие способы визуализации.
Во-вторых, полигон частот не позволяет точно определить значения между указанными точками графика. Это ограничение проистекает из того, что полигон частот представляет собой линии, соединяющие середины столбцов гистограммы. Если необходимо определить точную величину частоты для конкретного значения, следует обращаться к исходным данным.
Также следует отметить, что полигон частот обычно используется для представления категориальных данных, а не количественных. Он позволяет наглядно отобразить распределение частоты встречаемости каждой категории. Однако для анализа количественных данных может быть более удобно использовать другие методы, такие как диаграмма размаха или график плотности распределения.
Наконец, следует учитывать, что полигон частот является статическим представлением данных и не позволяет исследовать их взаимосвязи или зависимости. Для более глубокого анализа данных может потребоваться использование других статистических методов или создание интерактивных визуализаций.



