В геометрии существуют различные законы и теоремы, которые позволяют решать разнообразные задачи. Одна из таких теорем, которая является основой для многих доказательств, - это теорема о сумме углов треугольника. Согласно этой теореме, сумма всех углов в треугольнике равна 180 градусов.
Однако существуют треугольники, в которых некоторые углы могут быть равны между собой. Именно об этом факте и говорится, когда говорят о равных углах в треугольнике. Благодаря таким равенствам можно находить другие углы и стороны треугольника.
В нашей задаче известно, что угол ВАС равен 84 градусам. Теперь мы можем использовать знание о сумме углов треугольника, чтобы найти другие углы. Например, сумма углов ВАС и САВ должна быть равна 180 градусам. Зная значение угла ВАС, мы можем найти угол САВ, используя следующую формулу:
Итак, в треугольнике АВС угол САВ, а следовательно и угол ВAC, равны 96 градусам. Теперь у нас есть два равных угла и мы можем пойти дальше в доказательстве.
Свойства треугольника АВС
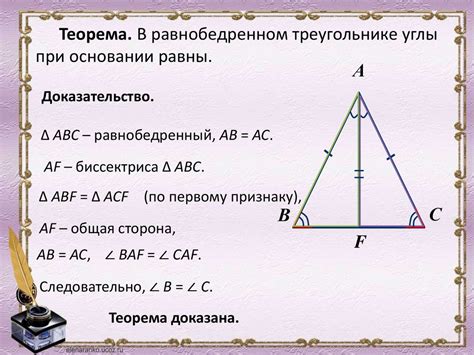
В треугольнике АВС известно, что Угол ВАС равен 84°. Согласно свойствам треугольника:
1. Сумма всех внутренних углов треугольника равна 180°. Следовательно, угол А равен 180° - 84° - угол С.
2. В треугольнике равнобедренным является тот треугольник, у которого две стороны равны. В нашем случае, угол ВАС не равняется 90°, поэтому треугольник АВС не является равнобедренным.
3. В треугольнике АВС сумма длин любых двух сторон всегда больше длины третьей стороны (неравенство треугольника). Например, в нашем случае стоит проверить, будет ли соблюдаться неравенство ВА + АС > ВС. Если да, то треугольник существует, если нет - то нет.
4. Треугольник АВС может быть разделен на два прямоугольных треугольника. Например, можно провести высоту из вершины В на сторону АС, тогда получим два прямоугольных треугольника: АВЕ и ВЕС. Где Е - точка пересечения высоты с основанием АС.
5. Угол В равен 180° - 84° - угол С.
6. Треугольник АВС может быть образован с помощью различных комбинаций сторон и углов. Например, если известны длины сторон ВА и ВС, а также величина угла между ними, то можно восстановить треугольник АВС.
Помимо указанных свойств, в треугольнике АВС могут быть и другие особенности, которые могут быть использованы, например, при решении задач на нахождение длин сторон, высот, площадей и т.д. Знание свойств треугольника АВС позволяет более глубоко и точно анализировать и решать задачи, связанные с этим треугольником.
Угловая величина ВАС
Угол ВАС является важным элементом треугольника АВС. Он помогает определить форму и свойства треугольника, такие как его тип (остроугольный, тупоугольный или прямоугольный) и соотношение между его сторонами.
Для нахождения угловой величины ВАС можно использовать различные методы. Например, если известны длины сторон треугольника и другие углы, можно воспользоваться теоремой синусов или косинусов. Также можно использовать геометрические свойства треугольника, такие как свойства параллельных линий или суммы углов треугольника.
Зная угловую величину ВАС, можно также рассчитать другие углы треугольника. Например, угол ВСА будет равен 180 - 84 = 96 градусов, так как сумма углов треугольника равна 180 градусов.
Угол ВАС также может быть использован для решения различных геометрических задач. Например, с его помощью можно определить высоту или медиану треугольника, вычислить площадь треугольника или найти длину некоторых его сторон.



