Один из самых интересных и важных вопросов в математике и программировании – это определение, является ли число степенью двойки. Существуют разные подходы к решению этой задачи, и они могут быть полезны в различных ситуациях.
Степень двойки имеет особые свойства и представляет собой число, которое может быть получено путем умножения двойки на себя несколько раз. Например, числа 1, 2, 4, 8, 16 и 32 являются степенями двойки.
Как же определить, является ли число степенью двойки? Существует несколько способов. Один из них – это использование битовой маски. Если число, которое мы проверяем, является степенью двойки, то оно будет иметь только один установленный бит. То есть его двоичное представление будет иметь вид 10000, 100000, 1000000 и т. д.
Что такое степень двойки и как ее определить?
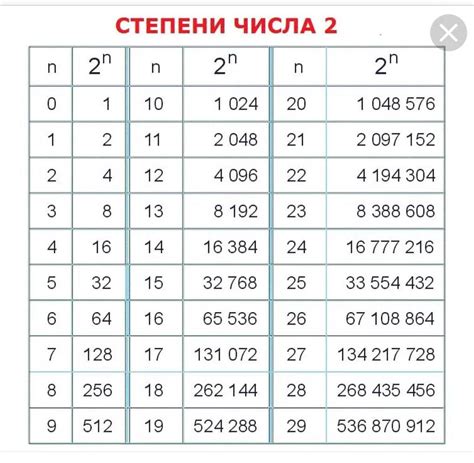
Существует несколько способов определить, является ли число степенью двойки:
- Способ первый: Найти логарифм числа по основанию 2. Если логарифм является целым числом, то исходное число является степенью двойки.
- Способ второй: Проверить, является ли число двоичным числом, состоящим только из единиц и одной единицы в двоичной записи. Если такое условие выполняется, то число является степенью двойки.
- Способ третий: При помощи битовых операций. Исходное число является степенью двойки, если оно положительное и имеет только одну единичную цифру в двоичной записи. Например, число 8 в двоичной записи представляется как 1000, где только одна цифра равна единице.
- Способ четвертый: Взять логарифм по основанию 2 от числа и проверить, является ли результат целым числом. Если да, то число является степенью двойки.
Используя один из этих способов, можно определить, является ли число степенью двойки и узнать его степень. Это полезно, например, при работе с алгоритмами, которые требуют обработку степеней двойки.
Числа, которые можно представить в виде степени двойки
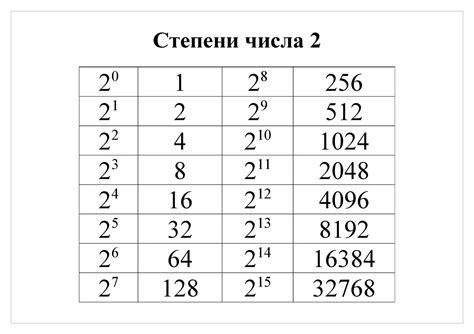
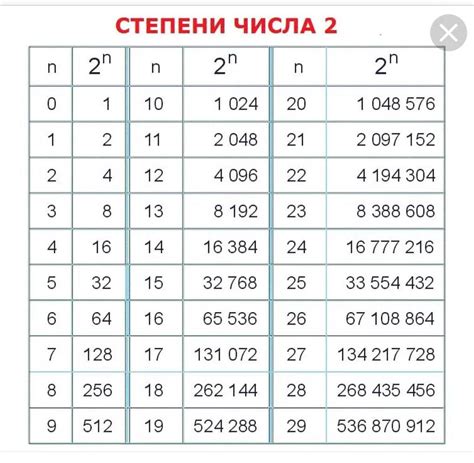
Числа, которые можно представить в виде степени двойки, называются степенями двойки или двоичными степенями.
Два - это самая маленькая степень двойки. Оно равно 2 в степени 1.
Чтобы определить, является ли число степенью двойки, нужно проверить, можно ли это число представить в виде 2 в окружении другого числа.
Степени двойки возрастают очень быстро. Например, 2 в степени 2 равно 4, 2 в степени 3 равно 8, 2 в степени 4 равно 16, и так далее.
Используя математическую нотацию, степень двойки может быть записана как 2n, где n - натуральное число.
Некоторые известные степени двойки:
- 21 = 2
- 22 = 4
- 23 = 8
- 24 = 16
- 25 = 32
Способы определения числа как степени двойки
| Способ | Описание |
|---|---|
| 1. Проверка с помощью битовой операции | Данное число можно представить в виде двоичного числа, где единица находится в единственном старшем бите, а все остальные биты равны нулю. Если число удовлетворяет этим условиям, то оно является степенью двойки. |
| 2. Проверка с помощью логарифма по основанию 2 | Если логарифм числа по основанию 2 является целым числом, то число является степенью двойки. Этот способ основан на свойствах логарифма и обращении этого свойства. |
| 3. Проверка с помощью деления на 2 | Если число является целым числом и при делении на 2 каждый раз получается целое число, то число является степенью двойки. |
Выбор способа определения числа как степени двойки зависит от ситуации и предпочтений программиста. Каждый из предложенных способов имеет свои преимущества и недостатки. Важно выбрать наиболее эффективный и удобный для конкретной задачи.
Быстрый способ определения числа как степени двойки
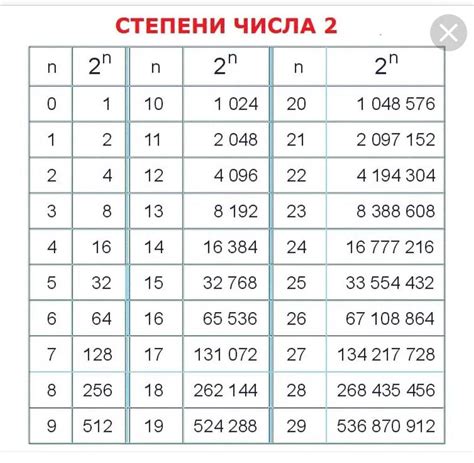
- Проверьте, равно ли число нулю. Если число равно нулю, оно не является степенью двойки.
- Проверьте, является ли число отрицательным. Если число отрицательное, оно не является степенью двойки.
- Проверьте, имеет ли число только одну установленную битовую позицию. Если число имеет более одной установленной битовой позиции, оно не является степенью двойки.
Чтобы выполнить проверку на наличие одной установленной битовой позиции, можно использовать побитовое И (&) между числом и его предыдущим значением (n-1). Если результат равен нулю, то число имеет только одну установленную битовую позицию и является степенью двойки.
Например, для числа 8:
- 8 = 1000 в двоичной системе счисления.
- 8 - 1 = 7 = 0111 в двоичной системе счисления.
- 8 & 7 = 0000 в двоичной системе счисления, что равно нулю.
Итак, число 8 является степенью двойки.
Этот быстрый способ определения числа как степени двойки может быть полезным при написании программ, которые требуют высокой скорости выполнения и эффективности.
Примеры чисел, являющихся степенями двойки:

- 2
- 4
- 8
- 16
- 32
- 64
- 128
- 256
- 512
- 1024
Числа, являющиеся степенями двойки, можно легко определить, поскольку они имеют особые свойства и повторяющиеся структуру. Они получаются путем умножения двойки саму на себя столько раз, сколько указано в показателе степени. Например, число 2 в степени 3 (2^3) равно 8, а число 2 в степени 4 (2^4) равно 16. Таким образом, все степени двойки представляют собой удвоение предыдущего числа, начиная с 2.
Как определить, что число не является степенью двойки?
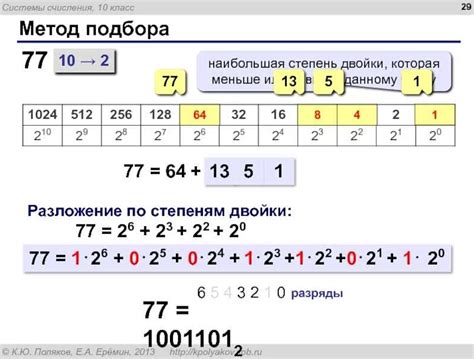
1. Способ №1: Проверить, делится ли число на 2 без остатка. Если не делится, то оно уже не является степенью двойки.
2. Способ №2: Выполнить побитовое "И" между числом и его предыдущим числом. Если результат не равен 0, то число не является степенью двойки.
3. Способ №3: Проверить количество единичных битов в двоичном представлении числа. Если их число больше одного, то число не является степенью двойки.
Воспользуйтесь одним из этих способов, чтобы определить, является ли число степенью двойки или нет.
Особые свойства чисел, являющихся степенями двойки

Числа, являющиеся степенями двойки, имеют некоторые особенности, которые можно использовать для их определения:
- Такие числа всегда являются положительными и целыми.
- Степень двойки всегда равна 2 в какой-то степени. Например, 2^0 = 1, 2^1 = 2, 2^2 = 4 и так далее.
- Числа-степени двойки всегда имеют только одну единичную цифру в двоичном представлении. Например, 1 (2^0) = 1 (в двоичной системе), 2 (2^1) = 10, 4 (2^2) = 100 и так далее.
- Если число является степенью двойки, то оно может быть выражено в виде 2^n (где n - некоторое целое число).
Используя эти свойства, можно легко определить, является ли число степенью двойки. Для этого нужно проверить, является ли число положительным, целым и имеет только одну единичную цифру в двоичном представлении. Также можно проверить, можно ли число выразить в виде 2^n для некоторого целого числа n.
Число 0: является ли оно степенью двойки?
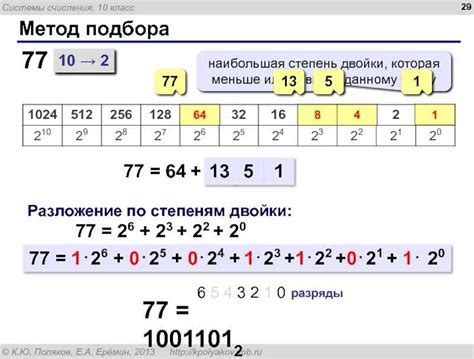
Степенью двойки называется число, полученное в результате возведения числа 2 в какую-либо целую степень. Например, 2^2 равно 4, 2^3 равно 8 и т.д. Однако, если мы рассмотрим 2^0, мы получим результат 1. Таким образом, можно сказать, что 1 является степенью двойки.
Что же происходит со значение 0? В математике 0 не относится к множеству натуральных чисел, степени двойки которых мы обычно рассматриваем. Поэтому 0 не считается степенью двойки.
Можно выразить это и таблицей:
| Число | Степень двойки? |
|---|---|
| 1 | Да |
| 2 | Да |
| 4 | Да |
| 8 | Да |
| 16 | Да |
| 32 | Да |
| 0 | Нет |
Зачем нужно знать, является ли число степенью двойки?
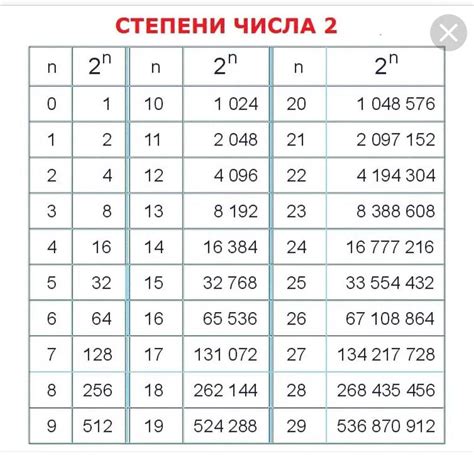
Во-первых, такая информация может использоваться в оптимизации алгоритмов и снижении вычислительной сложности. Если число является степенью двойки, то при выполнении операций возведения в степень или умножения на данное число можно использовать более эффективные алгоритмы и получить результат быстрее.
Во-вторых, знание того, является ли число степенью двойки, может быть полезным при работе с памятью и битовыми операциями. Например, при работе с буфером данных размер блока может быть оптимальным, если он является степенью двойки. Это связано с особенностями адресации и выравнивания в памяти компьютера.
Кроме этого, иногда требуется проверить, является ли количество элементов в массиве или коллекции степенью двойки. Это может быть полезным для оптимизации работы с данными, особенно при использовании алгоритмов, которые требуют размера степени двойки, например, в алгоритмах быстрого преобразования Фурье или при работе с деревьями.
Таким образом, знание того, является ли число степенью двойки, может помочь в оптимизации вычислений, улучшении производительности и более эффективной работе с данными.
Алгоритм определения числа как степени двойки
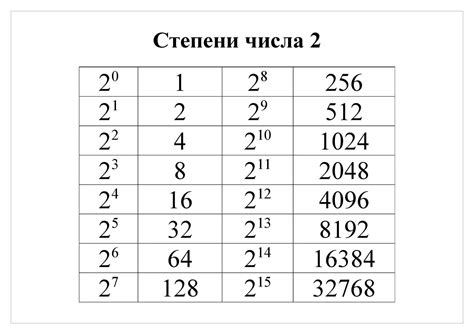
- Проверить, является ли число нулем или меньше нуля. Если это так, то число не является степенью двойки.
- Проверить, является ли число равным единице. Если это так, то число является степенью двойки (20 = 1).
- Далее, проверить, является ли число четным или нечетным.
- Если число нечетное, то оно точно не является степенью двойки.
- Если число четное, то необходимо его разделить на 2 и повторить шаг 3 с полученным результатом.
- Повторять шаг 5 до тех пор, пока не получится нечетное число.
- Если в результате получается 1, то исходное число является степенью двойки. В противном случае - не является.
Таким образом, данный алгоритм позволяет определить, является ли число заданной степенью двойки или нет, используя последовательное деление числа на 2 до получения нечетного числа или 1.
Применение определения числа как степени двойки в программировании
В программировании часто требуется проверить, является ли число степенью двойки, например, при работе с двоичными данными или при разработке алгоритмов, основанных на свойствах чисел, представленных в двоичной системе счисления.
Существует несколько способов определения числа как степени двойки. Одним из наиболее распространенных методов является проверка наличия только одной единицы в двоичном представлении числа. Если в числе есть только одна единица, то оно является степенью двойки.
Программно данное определение можно реализовать с помощью битовых операций. Воспользовавшись операцией побитового "И" между числом и его предшественником (числом, уменьшенным на 1), можно проверить, является ли число степенью двойки.
Пример кода на языке C++:
unsigned int number = 16;
bool isPowerOfTwo = (number & (number - 1)) == 0; В данном примере переменная "number" содержит значение, которое необходимо проверить. В переменную "isPowerOfTwo" записывается результат проверки: если число является степенью двойки, то переменная будет содержать значение "true", иначе - "false".
Такой подход к определению чисел как степеней двойки находит широкое применение в различных алгоритмах и задачах, связанных с обработкой двоичных данных, битовыми масками и другими аспектами программирования.



