Математика – это наука, которая ставит перед собой задачу изучить различные математические объекты и их свойства. Одним из основных объектов в математике является функция. Функция определяет зависимость одной величины от другой и играет важную роль во многих областях науки и жизни в целом.
Функция обычно записывается в виде f(x), где f – обозначение функции, а x – аргумент, при котором определяется значение функции. В данной статье мы рассмотрим функцию f(x)=5x+6 и найдем значение функции при различных значениях аргумента.
Что такое f(x) и как её найти?

Для нахождения значения функции f(x) по заданному значению переменной x используется алгоритм, заданный в определении функции. В данном случае функция f(x) задана выражением 5x+6, где x - переменная.
Для нахождения значения функции f(x) по заданному значению переменной x, необходимо подставить значение x в выражение 5x+6 и выполнить арифметические операции. Например, если x=2, то f(2)=5*2+6=16.
Таким образом, функция f(x)=5x+6 позволяет найти значение функции по заданному значению переменной x.
Что означает f(x) и зачем она нужна?

Функции широко применяются в различных областях, таких как физика, экономика, инженерия и информатика. Они позволяют описывать и анализировать разнообразные процессы и связи между переменными.
Основной причиной использования функций является их удобство и эффективность. С их помощью можно строить модели, прогнозировать результаты, решать уравнения и задачи оптимизации.
Кроме того, функции позволяют глубже понять и описать сложные процессы и явления в математике и науке в целом. Они являются основой для изучения анализа, алгебры, геометрии и других математических дисциплин.
Использование функций также упрощает и унифицирует обработку данных и расчеты. Они позволяют создавать более читаемый и структурированный код в программировании, упрощают работу с формулами и уравнениями.
Как найти f(x) для функции с линейной зависимостью?
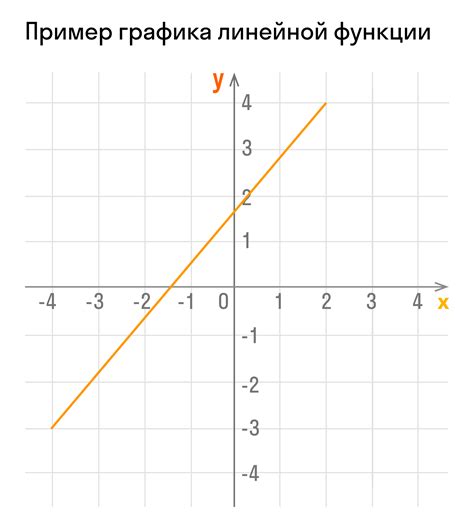
Для нахождения f(x) для функции с линейной зависимостью, необходимо применить уравнение прямой. В данном случае у нас есть функция f(x)=5x+6. Чтобы найти f(x), нужно взять значение x, умножить его на 5 и прибавить 6. Результатом будет значение функции f(x) для данного x.
Примеры вычисления f(x) для различных значений x
Для вычисления значения функции f(x)=5x+6 можно использовать различные значения переменной x. Ниже приведены несколько примеров:
1. Для x = 1:
f(1) = 5 * 1 + 6 = 5 + 6 = 11
2. Для x = 0:
f(0) = 5 * 0 + 6 = 0 + 6 = 6
3. Для x = -2:
f(-2) = 5 * (-2) + 6 = -10 + 6 = -4
4. Для x = 10:
f(10) = 5 * 10 + 6 = 50 + 6 = 56
Таким образом, значения функции f(x) будут различны для каждого значения переменной x. Это позволяет наглядно представить зависимость функции от входных параметров.
Как рассчитать f(x) для функции с квадратичной зависимостью?
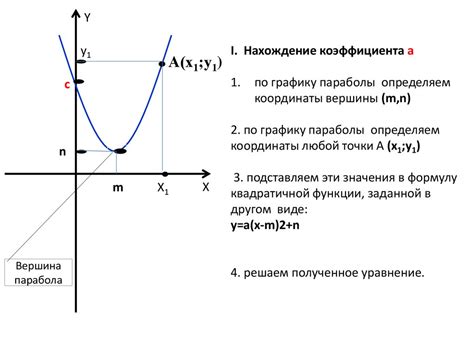
Для расчета значения f(x) для функции с квадратичной зависимостью, необходимо подставить конкретное значение переменной x в уравнение функции и выполнить вычисления.
Пример:
Рассмотрим функцию f(x) = 2x^2 - 3x + 1 и найдем значение f(3).
Для этого подставим x = 3 в уравнение:
f(3) = 2(3)^2 - 3(3) + 1 = 18 - 9 + 1 = 10.
Таким образом, f(3) = 10 для функции f(x) = 2x^2 - 3x + 1.
Аналогичным образом можно рассчитать значение функции для любого другого значения переменной x.
Используя указанный метод, можно определить точные значения f(x) для функции с квадратичной зависимостью при различных значениях переменной x.
Как использовать f(x) для построения графиков?
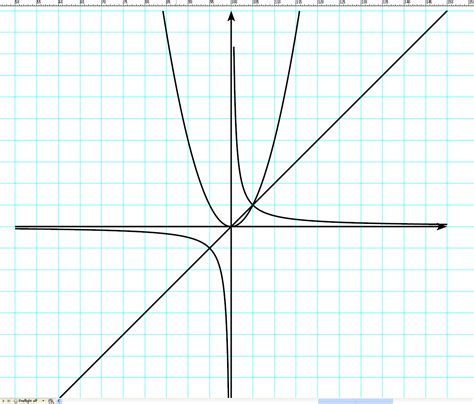
Функция f(x) представляет собой математическое выражение, которое может быть использовано для построения графика. График функции позволяет наглядно представить зависимость между переменной x и соответствующими значениями f(x).
Для построения графика f(x)=5x+6, необходимо:
| Шаг | Действие |
|---|---|
| 1 | Выбрать диапазон значений x, для которого будет строиться график. |
| 2 | Вычислить соответствующие значения функции f(x) для выбранных значений x. |
| 3 | Построить точки на координатной плоскости, где по оси x откладываются выбранные значения, а по оси y откладываются соответствующие значения f(x). |
| 4 | Соединить построенные точки линией, получив график функции f(x). |
Построив график функции f(x)=5x+6, можно проанализировать его свойства, такие как наклон, точка пересечения с осями координат, возрастание или убывание функции в заданном интервале значений x.
Важно отметить, что использование математических функций для построения графиков является важной частью анализа и визуализации данных, и может применяться в различных областях, включая физику, экономику, информатику и многие другие.
Как найти f(x) для функции с тригонометрической зависимостью?

Чтобы найти f(x) для функции с тригонометрической зависимостью, нужно использовать соответствующую формулу или свойство тригонометрии. Давайте рассмотрим пример функции f(x) с тригонометрической зависимостью и посмотрим, как ее найти.
Пусть у нас есть функция g(x) = sin(x), а мы хотим найти f(x) = g(x) + 2. Для этого нужно взять значение g(x), то есть sin(x), и прибавить 2. Получится функция f(x) = sin(x) + 2.
Аналогично можно найти f(x) для функций с другими тригонометрическими зависимостями, например, cos(x) или tan(x). Для этого нужно использовать соответствующие формулы или свойства тригонометрии.
Если у нас есть более сложная функция, состоящая из нескольких тригонометрических функций, мы можем использовать свойства тригонометрии, такие как сумма или разность аргументов, двойной аргумент, и т. д., чтобы упростить функцию и найти f(x).
Важно помнить, что при работе с функциями с тригонометрической зависимостью необходимо использовать правильные единицы измерения для аргументов и иметь в виду периодичность функций.
Таким образом, для нахождения f(x) для функции с тригонометрической зависимостью необходимо использовать соответствующие формулы или свойства тригонометрии и правильно работать с аргументами и единицами измерения.
Какие еще виды зависимости можно представить в виде f(x)?
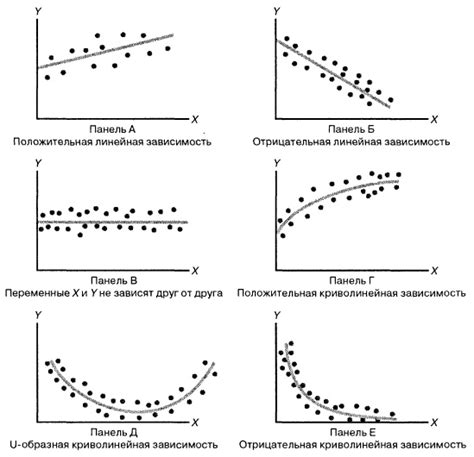
В общем случае, функция f(x) может иметь различные виды зависимости:
1) Линейная зависимость: f(x)=kx+b, где k и b - константы. Это наиболее простой вид зависимости, в котором значение y (f(x)) пропорционально значению x.
2) Квадратичная зависимость: f(x)=ax^2+bx+c, где a, b и c - константы. В этом случае, значение y (f(x)) зависит от квадрата значения x.
3) Экспоненциальная зависимость: f(x)=a*e^(bx), где a и b - константы, а e - число Эйлера. В этом случае, значение y (f(x)) возрастает (или убывает) экспоненциально с увеличением значения x.
4) Логарифмическая зависимость: f(x)=a*log(x)+b, где a и b - константы, а log - натуральный логарифм. В этом случае, значение y (f(x)) зависит от логарифма значения x.
5) Тригонометрическая зависимость: f(x)=a*sin(bx)+c, где a, b и c - константы, а sin - синус. В этом случае, значение y (f(x)) зависит от синуса значения x.
Это лишь некоторые примеры видов зависимостей, которые можно представить в виде функции f(x). В реальности, функции могут иметь бесконечное количество видов зависимостей в зависимости от конкретной задачи или явления.
Как использовать f(x) для решения задачи оптимизации?

Оптимизация заключается в поиске наилучшего решения в заданных условиях. Для использования функции f(x) в задаче оптимизации необходимо выполнить следующие шаги:
- Определить переменные: в задаче оптимизации нужно определить, какая переменная подлежит оптимизации. В данном случае переменная x является объектом оптимизации.
- Составить уравнение: на основе задачи оптимизации составляем уравнение, в котором функция f(x) будет выражать целевую функцию.
- Найти экстремумы: для решения задачи оптимизации нужно найти точки экстремума функции f(x), то есть максимумы или минимумы функции.
- Анализировать результаты: найденные точки экстремума позволяют анализировать оптимальные значения переменной x и соответствующие им значения функции f(x).
Для удобства решение задачи оптимизации можно представить в виде таблицы:
| Значение x | Значение f(x) |
|---|---|
| x1 | f(x1) |
| x2 | f(x2) |
| ... | ... |
Анализируя значения функции f(x) на различных значениях переменной x, можно найти оптимальное значение x, при котором достигается минимум или максимум функции.
Использование функции f(x) в задачах оптимизации может помочь в решении различных задач, таких как определение наиболее выгодного пути, максимизация или минимизация затрат, оптимальное распределение ресурсов и др.



