Неравенства являются одним из основных понятий в математике. Они используются для сравнения чисел и выражений, указывая на то, какое из них больше или меньше. Неравенства часто возникают при решении различных задач и играют важную роль в многих областях науки и промышленности.
Когда мы сталкиваемся с неравенствами, одной из ключевых задач является нахождение суммы целых решений. Целые решения неравенства - это значения переменных, которые удовлетворяют заданным условиям и являются целыми числами.
Для того чтобы найти сумму целых решений неравенства, необходимо применить определенные математические методы. Эти методы могут включать в себя перебор всех возможных значений переменных, использование алгоритмов и техник решения неравенств. Однако, в каждом конкретном случае необходимо выбирать тот метод, который наиболее подходит для решения задачи и получения точного результата.
Неравенства и их решения

Решение неравенств - это процесс нахождения всех значений переменной, которые удовлетворяют данному неравенству. Результатом решения неравенства может быть конкретное значение переменной или интервал значений.
Существует несколько типов неравенств, таких как линейные, квадратные, иррациональные, системы неравенств и так далее. В каждом случае требуется свой метод для решения неравенства.
Одним из методов решения неравенств является графический метод, при котором неравенство представляется на числовой оси в виде отрезка или интервала. Все значения переменной, которые находятся внутри этого интервала, удовлетворяют данному неравенству.
Другим методом является алгебраическое решение неравенства, при котором используются основные алгебраические операции, такие как сложение, вычитание, умножение и деление, чтобы выразить переменную и найти ее значения, удовлетворяющие неравенству.
Важно помнить, что при решении неравенств необходимо учитывать знак неравенства (больше, меньше, больше или равно, меньше или равно) и правила работы с этими знаками.
Сумма целых решений неравенств
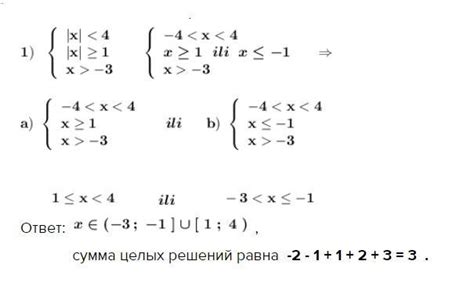
Для нахождения суммы всех целых решений неравенства ax + by
| x | y | x + y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 2 |
| -1 | 0 | -1 |
| 0 | -1 | -1 |
| -1 | -1 | -2 |
В данном случае, сумма всех целых решений неравенства будет равна 0 + 1 + 1 + 2 + (-1) + (-1) + (-2) = 0.
Таким образом, сумма целых решений неравенств может быть найдена с помощью таблицы, которая отображает значения x, y и их сумму.



