Производная – одно из важных понятий математического анализа. Она позволяет определить скорость изменения функции в каждой точке её области определения. В частности, производная функции заданной в виде x^2 может быть вычислена по формуле.
Обозначение производной функции f(x) по аргументу x часто записывают как f'(x), dy/dx или y'. Для функции y = x^2 формула определения производной будет выглядеть следующим образом:
d(y)/d(x) = 2x.
Определение производной функции y = x^2 означает, что скорость изменения значения функции в каждой точке равна удвоенному значению аргумента. Например, при x = 3 производная функции равна 2 * 3 = 6. Это означает, что значение функции x^2 меняется с удвоенной скоростью, когда аргумент изменяется на единицу.
Производная от x в квадрате: формула и примеры вычисления
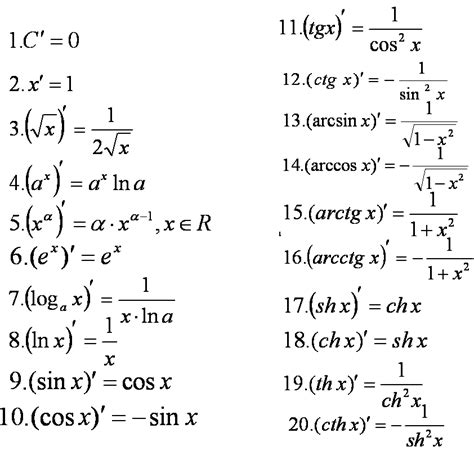
Производная от функции вида f(x) = x^2, где x возводится в квадрат, может быть вычислена с помощью простой формулы. Для этого нужно применить правило дифференцирования и найти производную этой функции.
Формула для вычисления производной функции f(x) = x^2 выглядит следующим образом:
f'(x) = 2x
Это означает, что производная функции f(x) = x^2 равна 2x. То есть, чтобы найти производную от функции вида x в квадрате, нужно умножить значение x на 2.
Например, если нужно найти производную от функции f(x) = 3x^2, то она будет равна:
f'(x) = 2 * 3x = 6x
Аналогично, для функции f(x) = 5x^2 производная будет:
f'(x) = 2 * 5x = 10x
Таким образом, чтобы найти производную от функции x в квадрате, нужно просто умножить значение x на 2. Это правило можно использовать для вычисления производных других функций, в которых встречается x в квадрате.
Изучаем производную

В случае функции вида f(x) = x^2, чтобы найти производную, используем формулу дифференцирования степенной функции. Для функции f(x) = x^n, производная равна n * x^(n-1).
| Исходная функция | Производная |
|---|---|
| f(x) = x^2 | f'(x) = 2x |
Например, для функции f(x) = x^2, производная будет f'(x) = 2x. То есть, если заданная функция представлена графически, то значение производной в каждой точке будет указывать на наклон касательной к этой точке. Так, производная f'(x) = 2x показывает, что в любой точке графика касательная будет иметь наклон, равный удвоенному значению этой точки.
Изучение производной является важным шагом для более глубокого понимания математического анализа и многих областей науки. Оно помогает в решении задач, связанных с оптимизацией, моделированием и прогнозированием изменений.
Формула производной для x в квадрате
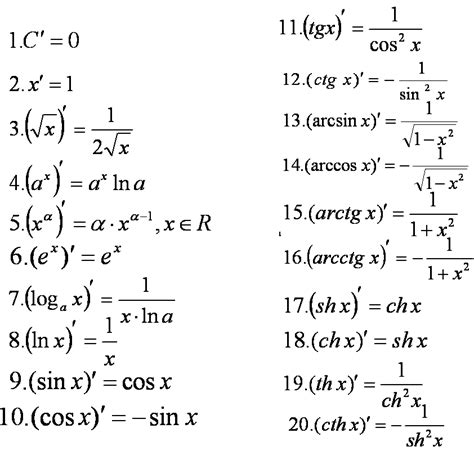
Производная функции x в квадрате вычисляется по известной формуле:
f'(x) = 2x
Эта формула указывает, что производная функции x в квадрате равна удвоенному значению аргумента. Другими словами, если у нас есть функция f(x) = x^2, то ее производная f'(x) будет равна 2x.
Например, чтобы вычислить производную функции f(x) = x^2 в точке x = 3, мы можем использовать формулу выше:
f'(3) = 2 * 3 = 6
Таким образом, производная функции f(x) = x^2 в точке x = 3 будет равна 6.
Примеры вычисления производной для x в квадрате
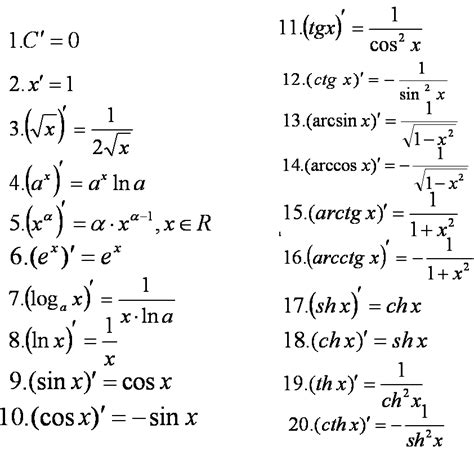
Рассмотрим несколько примеров вычисления производной функции f(x) = x2.
| Пример | Получившаяся производная |
|---|---|
| f(x) = x2 | f'(x) = 2x |
| f(x) = 3x2 | f'(x) = 6x |
| f(x) = (x + 1)2 | f'(x) = 2(x + 1) |
В первом примере производная функции f(x) = x2 равна f'(x) = 2x. Это означает, что при изменении значения переменной x на единицу, значение функции меняется вдвое больше.
Во втором примере, если f(x) = 3x2, то производная будет f'(x) = 6x. Здесь мы видим, что коэффициент перед x удваивается при взятии производной.
Третий пример немного отличается от предыдущих. Если f(x) = (x + 1)2, то производная будет f'(x) = 2(x + 1). В данном случае мы применяем правило дифференцирования сложной функции, где производная внутренней функции умножается на производную внешней функции.
Это лишь несколько примеров вычисления производной для функции x2. Используя правила дифференцирования, можно рассчитать производную для значительно более сложных функций. Понимание производных позволяет анализировать скорость изменения величины и находить экстремумы функций, что важно во множестве областей знания.



