График обратно пропорциональной функции – это визуальное представление зависимости между двумя переменными, где одна переменная увеличивается, а другая уменьшается в обратной пропорции. Обратно пропорциональная функция описывает такие отношения, где увеличение одной величины вызывает уменьшение другой.
На графике обратно пропорциональной функции можно наблюдать параболическую кривую, которая отклоняется от осей координат. Обычно она начинается в первом квадранте и стремится к положительной бесконечности в каждом из квадрантов.
Например, рассмотрим функцию y = k/x, где k – постоянное число. Если x увеличивается, то y уменьшается, и наоборот. На графике заметно, что кривая становится более пологой, когда x растет или уменьшается. При x = 0 график не определен из-за деления на ноль.
График обратно пропорциональной функции: объяснение и примеры
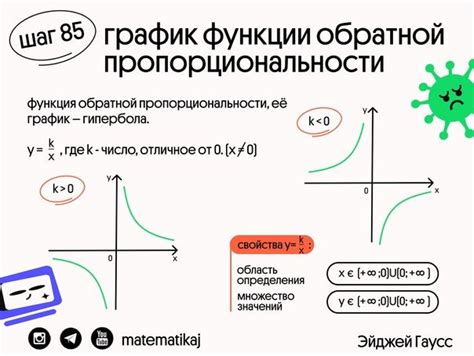
График обратно пропорциональной функции представляет собой гиперболу, это кривая, которая состоит из двух ветвей, расходящихся от оси координат. Одна ветвь графика находится в первой и третьей четвертях, а другая во второй и четвертой четвертях плоскости. Эти ветви стремятся к осям, но никогда ее не касаются.
Чтобы построить график обратно пропорциональной функции, необходимо иметь две переменные и их значения. Затем, используя эти значения, необходимо найти произведение двух переменных и проверить, что оно остается постоянным. Строим график, отмечая на координатной плоскости точки с соответствующими значениями переменных.
Например, рассмотрим обратно пропорциональную функцию y = k/x, где k - постоянный коэффициент. Если мы возьмем значения для x и y и умножим их, результат должен быть постоянным.
Давайте рассмотрим пример. Пусть мы решаем задачу нахождения времени, которое необходимо для пройдения определенного расстояния с постоянной скоростью. Если скорость постоянна, то время, необходимое для пройденного расстояния, обратно пропорционально расстоянию. Чем больше расстояние, тем меньше времени требуется.
Рассмотрим таблицу, где расстояние указано в километрах, а время - в минутах:
- Расстояние: 10, Время: 60
- Расстояние: 20, Время: 30
- Расстояние: 30, Время: 20
Для построения графика обратно пропорциональной функции, мы можем использовать эти значения. Построив график, мы увидим, что точки лежат на гиперболе, и чем больше расстояние, тем меньше время.
Используя график обратно пропорциональной функции, можно определить, как одна переменная изменится при изменении другой переменной, и наоборот. Это может быть полезно при решении различных задач, связанных с обратно пропорциональным отношением.
Определение и свойства
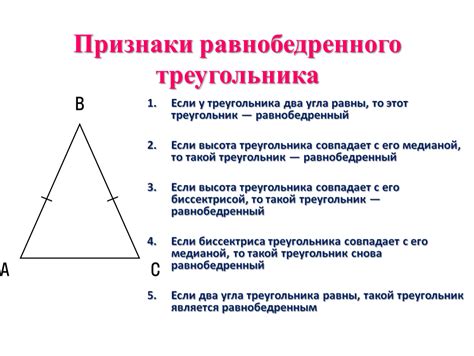
Основные свойства графика обратно пропорциональной функции:
- График всегда проходит через начало координат (0, 0), так как при x = 0 значение функции также равно 0.
- График является гиперболой и имеет две асимптоты: ось x (вертикальная) и ось y (горизонтальная).
- Пересечение графика с асимптотами не происходит.
- При увеличении значения x, значение y уменьшается, и наоборот, при уменьшении значения x, значение y увеличивается.
- График обратно пропорциональной функции всегда симметричен относительно точки (1/k, k), где k - коэффициент пропорциональности.
Изучая график обратно пропорциональной функции, можно определить его характеристики, такие как область определения и значения функции в различных точках, а также использовать его для решения различных задач, связанных с обратной пропорциональностью.
Особенности графика

График обратно пропорциональной функции имеет несколько характерных особенностей, которые помогают нам понять ее поведение и свойства.
Во-первых, график обратно пропорциональной функции всегда проходит через точку с координатами (1, k), где k - константа пропорциональности. Это означает, что при x = 1 значение y будет равно k.
Во-вторых, график такой функции является гиперболой, которая имеет две асимптоты: вертикальную и горизонтальную. Вертикальная асимптота проходит через точку x = 0, а горизонтальная асимптота - через y = 0. Эти асимптоты указывают на то, что функция не может достичь значения равного нулю или бесконечности.
В-третьих, график обратно пропорциональной функции всегда положительный в первом и третьем квадрантах, и отрицательный во втором и четвертом квадрантах.
И, наконец, график обратно пропорциональной функции сужается, когда x увеличивается, и расширяется, когда x уменьшается. Это свидетельствует о том, что при увеличении значения x, значение y уменьшается, и наоборот.
Графическое представление
На графике обратно пропорциональной функции можно наблюдать следующие особенности:
- Кривая всегда проходит через точку (1, k), где k – коэффициент пропорциональности.
- По мере увеличения значения x, значение y уменьшается, и наоборот. То есть, при увеличении одной переменной, другая уменьшается в обратной пропорции.
- График никогда не пересекает оси координат. Он всегда находится во второй и четвертой четверти координатной плоскости.
Например, если уравнение функции представлено как y = k/x, где k – постоянная величина, то график этой функции будет иметь вид гиперболы с вертикальной и горизонтальной асимптотами и кривой, проходящей через точку (1, k).
Графическое представление обратно пропорциональной функции помогает визуализировать взаимосвязь между двумя переменными и позволяет увидеть, как одна переменная изменяется при изменении другой. Кривая гиперболы может служить важным инструментом для анализа данных и предсказания трендов.
Зависимость между переменными
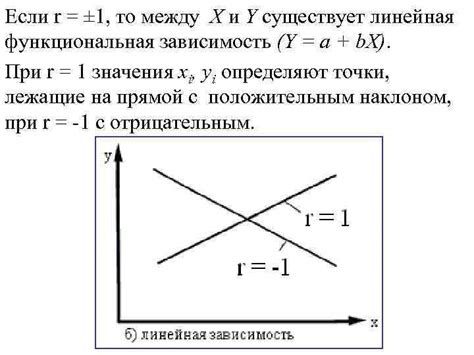
График обратно пропорциональной функции отражает зависимость между двумя переменными. В такой функции одна переменная изменяется в обратной пропорции к другой переменной. Это означает, что при увеличении одной переменной значение другой переменной уменьшается и наоборот.
Зависимость между переменными может быть представлена в виде графика, который показывает, как одна переменная влияет на другую. На графике обратно пропорциональной функции можно увидеть, что точки лежат на одной гиперболе.
Когда одна переменная увеличивается, график обратно пропорциональной функции смещается вниз и вправо. Когда одна переменная уменьшается, график смещается вверх и влево. Таким образом, график обратно пропорциональной функции состоит из двух ветвей, которые симметрично расположены относительно вертикальной оси симметрии.
Изучение зависимости между переменными позволяет понять, как изменения одной переменной влияют на другую. Например, при анализе экономических данных можно исследовать, как изменение цены товара влияет на его спрос и предложение.
Важно учитывать, что график обратно пропорциональной функции может иметь ограничения и не всегда быть применимым для описания зависимости между переменными. Поэтому, при анализе данных и построении графиков, необходимо применять различные методы и модели, чтобы получить более точные и полные результаты.
Интерпретация графика
График обратно пропорциональной функции представляет собой гиперболу, которая имеет следующие характерные особенности:
- График проходит через начало координат (точку (0, 0)).
- При увеличении значения одной переменной, значение другой переменной уменьшается.
- При уменьшении значения одной переменной, значение другой переменной увеличивается.
- График обратно пропорциональной функции не имеет асимптот и может быть ограничен только значением непропорциональной переменной.
Например, если рассмотреть график обратно пропорциональной функции, описывающей зависимость между скоростью движения автомобиля и временем, которое он затрачивает на преодоление заданного расстояния, можно заметить, что при увеличении скорости автомобиля, время, затрачиваемое на преодоление расстояния, уменьшается. Наоборот, при уменьшении скорости автомобиля, время увеличивается.
Интерпретация графика обратно пропорциональной функции позволяет легко понять, как изменение одной переменной влияет на другую. Она может быть полезным инструментом для прогнозирования и принятия решений в различных областях, таких как экономика, физика, математика и т. д.
Примеры из реальной жизни

График обратно пропорциональной функции можно встретить во многих ситуациях в реальной жизни. Вот несколько примеров:
| Пример | Объяснение |
|---|---|
| Текущая скорость и время путешествия | Если вы путешествуете на поезде или на автомобиле, чем выше скорость, тем быстрее вы достигнете места назначения. В этом случае график будет показывать, что время путешествия уменьшается по мере увеличения скорости. |
| Количество рабочих и время, необходимое для выполнения задачи | В некоторых сферах работы, например, на производстве, время, необходимое для выполнения задачи, уменьшается с увеличением числа рабочих, так как большее количество людей может выполнить задачу быстрее. |
| Количество света и расстояние до источника освещения | Когда вы находитесь ближе к источнику света, вы получаете больше света, а когда вы удаляетесь от него, количество света уменьшается. График обратно пропорциональной функции в этом случае будет показывать, что количество света уменьшается по мере увеличения расстояния до источника. |
Это лишь несколько примеров, которые помогут вам понять, как работает график обратно пропорциональной функции в реальной жизни. Важно запомнить, что график такой функции представляет собой гиперболу, которая имеет форму двух ветвей, расходящихся от вертикальной оси.
Применение графика в различных областях

Графики обратно пропорциональных функций имеют множество практических применений и находят широкое применение в различных областях. Вот несколько примеров использования графика обратно пропорциональной функции:
1. Физика и наука:
Графики обратно пропорциональных функций используются для моделирования различных физических явлений. Например, в законе Гука для пружинной системы сила, действующая на пружину, обратно пропорциональна ее удлинению. График этой функции позволяет лучше понять зависимость между силой и удлинением пружины.
2. Экономика:
В экономике графики обратно пропорциональных функций используются для анализа зависимостей между различными экономическими показателями. Например, зависимость между ценой товара и спросом на него обычно является обратно пропорциональной. График такой функции помогает определить оптимальную цену, при которой спрос на товар будет наибольшим.
3. Финансы:
В финансовой аналитике графики обратно пропорциональных функций используются для оценки рисков и доходности различных инвестиционных проектов. Например, график зависимости между длительностью инвестиции и доходностью может помочь определить оптимальный срок инвестирования.
4. Медицина:
Графики обратно пропорциональных функций широко применяются в медицине для анализа зависимостей между различными медицинскими показателями. Например, зависимость между количеством времени, затраченного на тренировки, и силой мышц может быть обратно пропорциональной. График такой функции помогает определить оптимальную длительность тренировок для достижения наилучших результатов.
Это лишь некоторые примеры применения графиков обратно пропорциональных функций в различных областях. Уникальные особенности и преимущества таких графиков делают их незаменимыми инструментами для понимания и анализа разнообразных зависимостей.
Сравнение с другими типами графиков

График обратно пропорциональной функции имеет определенные особенности, которые отличают его от других типов графиков.
В отличие от графика прямой пропорциональности, график обратно пропорциональной функции имеет форму гиперболы. Это значит, что при увеличении одной переменной, другая переменная уменьшается, и наоборот. На графике гиперболы видно, что кривая стремится к двум осям координат, но никогда не достигает их.
Сравнивая график обратно пропорциональной функции с графиком линейной функции, можно сказать, что график обратно пропорциональной функции всегда показывает отрицательную зависимость между переменными, в то время как график линейной функции может иметь как положительную, так и отрицательную зависимость.
Также стоит отметить, что график обратно пропорциональной функции имеет асимптоты – прямые, которые график никогда не пересекает. Асимптоты являются границами, к которым стремится график, но никогда не достигает их. В случае графика обратно пропорциональной функции, асимптоты находятся по обе стороны от оси координат, расположены под углом с осью и образуют четверть эллипса.
| Тип графика | Особенности |
|---|---|
| Обратно пропорциональная функция | Форма графика - гипербола, отрицательная зависимость, наличие асимптот |
| Прямая пропорциональность | Форма графика - прямая линия, положительная или отрицательная зависимость, отсутствие асимптот |
| Линейная функция | Форма графика - прямая линия, положительная или отрицательная зависимость, отсутствие асимптот |
Таким образом, график обратно пропорциональной функции отличается от других типов графиков своей формой, знаком зависимости и наличием асимптот.
Обратно пропорциональная функция описывает зависимость между двумя переменными в таком виде, что при увеличении одной переменной, вторая переменная уменьшается пропорционально. Уравнение такой функции можно записать в виде y = k/x, где y – зависимая переменная, x – независимая переменная, и k – коэффициент пропорциональности.
График обратно пропорциональной функции имеет несколько характерных особенностей. Во-первых, он всегда проходит через точку (1, k) и стремится к осям координат, но никогда не пересекает их. Во-вторых, при увеличении значения независимой переменной x, значение зависимой переменной y уменьшается. И наоборот, при уменьшении x, y увеличивается.
Примеры графиков обратно пропорциональных функций могут быть найдены в различных сферах жизни. Например, расстояние, которое можно проехать на заданном количестве топлива, будет обратно пропорционально расходу топлива на единицу пути. Также, скорость движения тела в воздухе будет уменьшаться при увеличении площади перпендикулярного сечения этого тела.
| x | y |
|---|---|
| 1 | k |
| 2 | k/2 |
| 3 | k/3 |
| 4 | k/4 |
Из этой таблицы также видно, что при увеличении значения x, значение y уменьшается. Это подтверждает обратную пропорциональность между x и y в этой функции.
Важно помнить, что график обратно пропорциональной функции может иметь различные формы, в зависимости от значения коэффициента пропорциональности и специфики задачи. Однако, главная характеристика такого графика – уменьшение значения одной переменной при увеличении другой переменной.



