Алгебра – одна из основных математических дисциплин, изучающая абстрактные структуры и операции, лежащие в основе многих наук. Строение и свойства объектов в алгебре могут быть формализованы и изучены при помощи математических методов и инструментов.
Одним из основных понятий, занимающих важное место в алгебре, является функциональная зависимость. Она позволяет определить, как одни переменные зависят от других в рамках математической модели. Функциональные зависимости активно используются в различных областях науки, включая информатику, статистику, базы данных и другие. Формализация функциональных зависимостей позволяет решать разнообразные задачи, связанные с анализом и прогнозированием различных процессов и явлений.
В данной статье будет рассмотрена тема формализации функциональных зависимостей. Мы рассмотрим основные понятия и определения, а также исследуем различные методы и подходы к формализации функциональных зависимостей. Также мы рассмотрим примеры применения формализованных функциональных зависимостей в реальных задачах и обсудим их практическую значимость.
Функциональные зависимости и их значение в алгебре

Функциональные зависимости полезны для анализа и решения различных задач, таких как определение области допустимых значений переменных, построение математических моделей и прогнозирование результатов. Они позволяют установить, как изменение входных данных повлияет на выходные данные и помогают предсказать поведение системы или процесса.
Таблицы с функциональными зависимостями часто используются для визуализации этих отношений. Каждая функциональная зависимость представляется в виде строки таблицы, где переменные и функции записываются в ячейках соответствующего столбца. Такие таблицы могут быть легко преобразованы и использованы для проведения операций алгебры, таких как вычисление значений функций при заданных входных данных или поиск значений, удовлетворяющих определенным условиям.
Понимание функциональных зависимостей и умение правильно формализировать их являются важными навыками в алгебре. Они помогают упростить и структурировать математические модели, улучшить точность и надежность вычислений, а также облегчить анализ и понимание взаимосвязей между переменными и функциями.
| Переменная X | Переменная Y | Функция F |
|---|---|---|
| x1 | y1 | F(x1, y1) |
| x2 | y2 | F(x2, y2) |
| x3 | y3 | F(x3, y3) |
В приведенной выше таблице показан пример функциональных зависимостей между переменными X и Y, а также функцией F. Каждое значение переменных X и Y соотносится с определенным значением функции F, представляя собой функциональную зависимость. Такая таблица может быть использована для работы с этими зависимостями, анализа их свойств и проведения соответствующих операций алгебры.
Примеры функциональных зависимостей в математике
| Пример | Функциональная зависимость |
|---|---|
| Пример 1 | Уравнение окружности: x^2 + y^2 = r^2. Зависимость y от x явно задана уравнением окружности. |
| Пример 2 | Бинарное отношение: множество пар чисел, где первое число является квадратом второго числа. Зависимость задается отношением "быть квадратом". |
| Пример 3 | Геометрическая прогрессия: a_n = a_1 * r^(n-1), где a_n - n-й член прогрессии, a_1 - первый член прогрессии, r - знаменатель прогрессии. Зависимость a_n от n задается формулой геометрической прогрессии. |
Эти примеры демонстрируют различные функциональные зависимости в математике. Они помогают понять, как входные значения влияют на результат функции и как описать эту зависимость формально.
Формальное определение функциональной зависимости

Формально, функциональная зависимость записывается в виде F: X → Y, где F – множество функциональных зависимостей, X и Y – множества атрибутов. Это означает, что для любых двух кортежей t1 и t2, если все атрибуты из X в кортежах t1 и t2 имеют одинаковые значения, то все атрибуты из Y также имеют одинаковые значения в этих кортежах.
Функциональные зависимости являются важным инструментом в проектировании баз данных. Они позволяют описывать связи между атрибутами и обеспечивать целостность данных в базе.
| Атрибуты X | Атрибуты Y |
|---|---|
| A | B |
| C | D |
| E | F |
В таблице представлен пример функциональной зависимости, где атрибуты A, C и E определяют значения атрибутов B, D и F соответственно.
Формализация функциональных зависимостей в алгебре
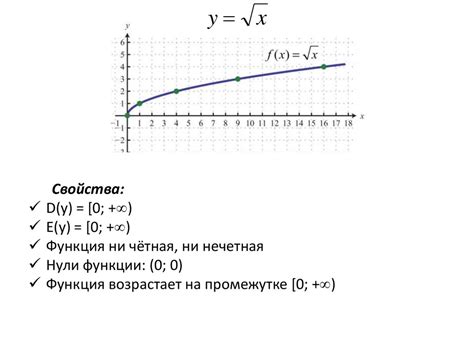
Формализация функциональных зависимостей состоит из двух ключевых понятий: левой и правой частей. Левая часть представляет собой множество атрибутов, от которых зависит другое множество атрибутов, которое называется правой частью.
Функциональная зависимость записывается как A → B, где A - левая часть, а B - правая часть. Это означает, что для каждого значения атрибутов в множестве A, существует только одно значение атрибутов в множестве B.
Формализация функциональных зависимостей имеет свои особенности. Например, она позволяет нам определить ключевой атрибут или соотношение между несколькими атрибутами. Кроме того, она может помочь нам избежать избыточности данных и улучшить производительность базы данных.
Виды формализации функциональных зависимостей

Функциональные зависимости играют важную роль в алгебре и базах данных, поскольку они определяют отношения между атрибутами. Для формализации функциональных зависимостей используются различные подходы и методы. В этом разделе рассмотрим несколько видов формализации функциональных зависимостей.
1. Функциональные зависимости в виде уравнений: Функциональные зависимости могут быть представлены в виде уравнений, где один атрибут зависит от других. Например, если у нас есть атрибуты А, B и С, и атрибут С зависит от атрибутов А и B, тогда уравнение будет выглядеть следующим образом: С = f(A, B).
2. Множественные функциональные зависимости: В некоторых случаях атрибут может зависеть от нескольких других атрибутов. В этом случае говорят о множественных функциональных зависимостях. Например, если атрибут С зависит от атрибутов А, В и D, тогда это будет множественная функциональная зависимость и она может быть формализована как С = f(A, B, D).
3. Функциональные зависимости в виде таблицы: Другой способ формализации функциональных зависимостей - это представление в виде таблицы, где каждая строка представляет собой отношение между атрибутами. В этой таблице каждый столбец представляет атрибут, а каждая ячейка содержит информацию о зависимостях между атрибутами.
4. Функциональные зависимости в виде графа: Графический подход также может использоваться для формализации функциональных зависимостей. В этом случае каждый атрибут представляется вершиной, а зависимости между атрибутами - ребрами графа. Такая формализация позволяет легко визуализировать и анализировать зависимости между атрибутами.
Каждый из этих подходов имеет свои преимущества и недостатки и может быть использован в зависимости от конкретной задачи и контекста.
Использование матриц для формализации функциональных зависимостей
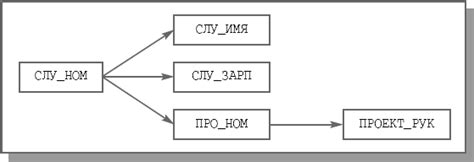
В контексте функциональных зависимостей матрицы могут быть использованы для представления и описания различных видов связей, таких как линейные, экспоненциальные или логарифмические. Это позволяет анализировать их влияние на другие переменные и оценить их важность в контексте задачи.
Каждая строка матрицы представляет собой набор значений переменных, а каждый столбец - набор значений других переменных, от которых зависит данная переменная. Таким образом, различные функциональные зависимости между переменными могут быть представлены в матричной форме.
Матрицы также позволяют выявить зависимости между рассматриваемыми переменными и дать возможность принять информированные решения на основе анализа данных. Они помогают понять, какие переменные имеют наибольший вклад в результаты и как изменение значений одной переменной может повлиять на другие переменные.
Таким образом, использование матриц для формализации функциональных зависимостей позволяет более точно и наглядно анализировать их влияние и принимать обоснованные решения на основе этого анализа.
Применение формализации функциональных зависимостей

Формализация функциональных зависимостей играет важную роль в алгебре и базах данных. Она позволяет явно описать и структурировать связи между данными, что упрощает их анализ и обработку.
Применение формализации функциональных зависимостей имеет широкий спектр приложений. Например, в разработке баз данных она позволяет установить соответствие между атрибутами таблицы и определить, какие зависимости между ними существуют. Это особенно полезно при проектировании новых систем или внесении изменений в существующие.
Кроме того, формализация функциональных зависимостей используется при оптимизации запросов в базах данных. Поиск истинных функциональных зависимостей позволяет улучшить производительность запросов, так как можно избежать необходимости обращения к лишним данным.
Другим примером применения формализации функциональных зависимостей является обнаружение и устранение аномалий при нарушении нормализации данных. Поиск и устранение функциональных зависимостей позволяет улучшить качество данных, избежать дублирования и противоречий.
Кроме приведенных примеров, формализация функциональных зависимостей также активно применяется в области машинного обучения, анализа данных и построения моделей. Она помогает выявлять и описывать закономерности и взаимосвязи между переменными, что позволяет облегчить задачу предсказания и прогнозирования.
Таким образом, формализация функциональных зависимостей является мощным инструментом, который находит применение во многих областях. Она позволяет описать и структурировать функциональные связи между данными, что упрощает их анализ, обработку и оптимизацию.
Анализ данных с использованием формализованных функциональных зависимостей

Для проведения анализа данных с использованием формализованных функциональных зависимостей необходимо выполнить следующие шаги:
- Изучение исходных данных: необходимо изучить имеющиеся данные и определить переменные, между которыми могут существовать функциональные зависимости.
- Построение графа зависимостей: на основе изученных данных нужно построить граф зависимостей, отображающий связи между переменными.
- Формализация зависимостей: на основе графа зависимостей нужно сформулировать формальные функциональные зависимости между переменными.
- Проверка зависимостей: необходимо проверить, являются ли сформулированные зависимости корректными на имеющихся данных.
- Использование зависимостей: после проверки зависимостей, они могут быть использованы для анализа и предсказания значений переменных.
Использование формализованных функциональных зависимостей позволяет упростить анализ данных и сделать его более надежным. Этот метод может применяться в различных областях, таких как наука, экономика, медицина и другие.
Важно помнить, что использование формализованных функциональных зависимостей требует аккуратности и проверки полученных результатов на реальных данных.
Использование формализации функциональных зависимостей в проектировании баз данных

Применение формализации функциональных зависимостей позволяет:
- Уточнить структуру данных: Использование функциональных зависимостей позволяет определить, какие атрибуты зависят от других, и помогает разделить данные на более мелкие и логически независимые части. Это улучшает структуру базы данных и делает ее более понятной и легкой в использовании.
- Предотвратить избыточность данных: Формализация функциональных зависимостей помогает выявить повторяющиеся атрибуты и связи в базе данных. Исправление избыточности данных позволяет сократить объем хранимых данных и улучшить производительность базы данных.
- Обеспечить целостность данных: Функциональные зависимости помогают определить требования к целостности данных и обеспечить их соблюдение. Например, они могут быть использованы для определения правил валидации данных или для установления ограничений на изменение определенных атрибутов.
- Упростить процесс изменения структуры базы данных: При изменении структуры базы данных, использование формализации функциональных зависимостей помогает определить, какие атрибуты и связи будут затронуты. Это упрощает процесс модификации базы данных и помогает предотвратить потерю данных или нарушение целостности данных.
В целом, использование формализации функциональных зависимостей в проектировании баз данных способствует созданию логичных, эффективных и надежных баз данных. Это важный инструмент для разработчиков и администраторов баз данных, который помогает управлять связями между данными и обеспечивать их правильность и целостность.



