Доказательство равенства отрезков является одной из базовых задач в геометрии. Оно требует применения определенных приемов и способов, чтобы убедительно и аргументированно установить, что два отрезка равны друг другу. В данной статье рассмотрим основные приемы, которые помогут школьникам 7 класса успешно решать подобные задачи.
Еще один способ доказательства равенства отрезков - это свойство симметрии. Если отрезки представляют собой две части одной и той же линии, и на них можно провести прямую взаимно однозначное соответствие точек, то они равны. Другими словами, если приложить один отрезок к другому и увидеть, что они полностью совпадают, то можно утверждать их равенство.
Как доказать, что отрезки равны

В геометрии существует несколько способов доказать, что два отрезка равны друг другу. Это важное утверждение, так как на равенстве отрезков базируется множество последующих математических доказательств и построений.
Первый способ - использование правила о равенстве сторон треугольника. Если мы можем построить треугольник, в котором две стороны равны соответствующим отрезкам, то по правилу о равенстве сторон треугольника можно утверждать, что и сами отрезки равны.
Третий способ - использование определения равенства отрезков. Определение равенства отрезков гласит, что два отрезка равны, если они имеют одинаковую длину. Поэтому, если мы можем непосредственно измерить два отрезка и получить одинаковую длину, то это является доказательством их равенства.
В зависимости от задачи и условий, можно выбрать наиболее удобный способ для доказательства равенства отрезков. Важно помнить, что доказательство равенства отрезков должно быть строго и аргументировано, чтобы быть признанным корректным.
Метод переноса
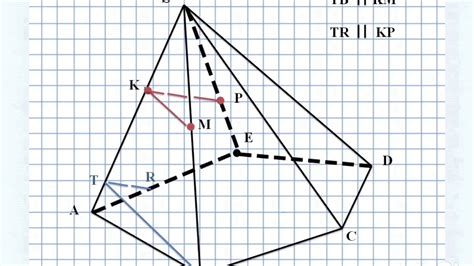
Для применения метода переноса необходимо знать следующие шаги:
- Выбрать точку переноса, которую обозначим буквой О.
- Провести от точки О прямую, параллельную отрезку, докажем это с помощью аксиомы о существовании параллельной прямой.
- Из точки O провести отрезок, равный данному отрезку, а также провести отрезок, равный параллельному отрезку.
- В результате, мы имеем два равных треугольника: один с вершинами в точке O, а другой с вершинами в точках начала и конца двух равных отрезков.
- Согласно теореме о равенстве треугольников, если два треугольника равны, то и их стороны равны. Следовательно, отрезки, имеющие начала и концы в равных точках, равны.
Метод переноса является простым и эффективным способом доказательства равенства отрезков. Он основывается на известных теоремах геометрии и позволяет подтвердить равенство отрезков с помощью конструктивных шагов.
Данный метод может быть использован для решения различных геометрических задач, требующих доказательства равенства отрезков. Он помогает структурировать и систематизировать процесс доказательства и обоснования геометрических свойств.
| Преимущества | Недостатки |
|---|---|
|
|
Метод сравнения длин

Шаги выполнения метода сравнения длин следующие:
- Измерьте длину первого отрезка, используя линейку или масштабную линейку.
- Измерьте длину второго отрезка с помощью тех же инструментов.
Важно помнить, что для корректного сравнения отрезков необходимо использовать одну и ту же единицу измерения.
Метод сравнения длин основан на простом, но эффективном принципе и является одним из самых доступных способов доказательства равенства отрезков.
Метод построения равных отрезков
Для доказательства равенства двух отрезков можно использовать метод построения равных отрезков. Этот метод основан на использовании компаса и линейки.
1. Возьмите линейку и на ней отметьте начало отрезка. Проведите прямую линию через начало отрезка.
2. Установите конец линейки на начало отрезка и поверните линейку до тех пор, пока она не пересечет прямую линию, проведенную на первом шаге. Отметьте эту точку на линейке.
3. Проведите отмеченную точку через конец отрезка так, чтобы прямая линия проходила через него.
4. Установите компас так, чтобы его одна ножка находилась в начале отрезка, а другая ножка находилась на прямой линии, проведенной через отмеченную точку из предыдущего шага.
5. Не меняя размера компаса, перенесите его другую ножку на прямую линию, проходящую через конец отрезка. Отметьте точку на этой линии.
6. Соедините отмеченную точку с началом отрезка. Полученная прямая линия будет равна исходному отрезку.
Таким образом, если полученная прямая линия совпадает с другим отрезком, то можно утверждать, что отрезки равны. Метод построения равных отрезков является надежным и точным способом доказательства равенства двух отрезков.
Использование косинуса
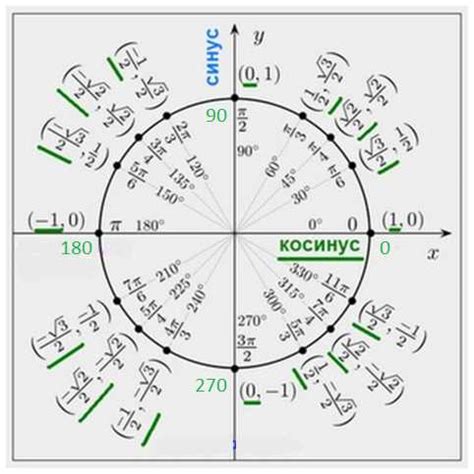
Если нам даны координаты четырех точек на плоскости, можно использовать тригонометрические функции, в частности косинус, для доказательства равенства отрезков.
Для этого мы можем использовать формулу косинуса для вычисления угла между двумя отрезками:
cos(α) = (AB · BC) / (|AB| * |BC|)
где AB и BC - векторы, представляющие данные отрезки, α - угол между ними.
Если косинус угла α равен 1, то отрезки AB и BC равны. Это связано с тем, что косинус 0° равен 1.
Таким образом, используя формулу косинуса, мы можем доказать равенство отрезков, если угол между ними равен 0° или 180°.
Применение теоремы Пифагора
При применении теоремы Пифагора, необходимо убедиться, что треугольник является прямоугольным. Если известны длины двух сторон треугольника, можно использовать теорему Пифагора для подтверждения равности третьей стороны.
Например, рассмотрим треугольник ABC, где AB и BC - катеты, а AC - гипотенуза. Если известны длины сторон AB и BC, то можно применить теорему Пифагора следующим образом:
- Возвести в квадрат длины стороны AB и BC: AB2 и BC2.
- Просуммировать полученные значения: AB2 + BC2.
- Возвести в квадрат длину гипотенузы AC.
Применение теоремы Пифагора позволяет доказывать равенство отрезков на основе известных длин сторон прямоугольного треугольника. Метод можно использовать как самостоятельно, так и в сочетании с другими способами доказательства равенства отрезков.
Угол между отрезками
Угол между отрезками можно найти с помощью геометрических методов:
- Используйте теорему косинусов: согласно этой теореме, квадрат длины третьего отрезка равен сумме квадратов длин двух других отрезков минус удвоенное произведение этих отрезков на косинус угла между ними.
- Примените формулу скалярного произведения: скалярное произведение двух векторов равно произведению модулей векторов на косинус угла между ними. Для нахождения угла между отрезками используйте обратную функцию косинуса.
Как только у вас есть угол между отрезками, вы можете проверить, является ли он прямым (90 градусов), остроугольным (менее 90 градусов) или тупым (более 90 градусов).
Зная угол между отрезками, вы также можете проверить их параллельность или перпендикулярность.
Угол между отрезками - важный инструмент в геометрии, который помогает определить свойства и отношения между отрезками и фигурами.
Проекции отрезков
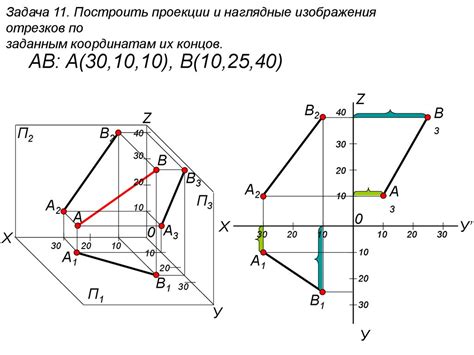
Проекция отрезка на прямую - это отрезок, который получается пересечением его с прямой, проведенной перпендикулярно данной прямой.
Чтобы доказать равенство двух отрезков с помощью проекций, необходимо:
- Провести прямую, перпендикулярную данной прямой, на которой лежат отрезки.
- Найти проекции каждого из отрезков на эту прямую.
- Сравнить длины полученных проекций.
Проекции отрезков используются в различных областях геометрии и физики. Например, для измерения длин отрезков на плоскости или на наклонных поверхностях.
Использование проекций отрезков является одним из эффективных способов доказательства равенства отрезков и позволяет упростить решение геометрических задач.



