Понятие перпендикулярности является одним из основных в геометрии, и его применение находит во многих областях науки и техники. В частности, в задачах по поиску различных свойств четырехугольников весьма полезно знать, как доказать взаимную перпендикулярность их диагоналей.
Для начала, необходимо уяснить, что диагональ - это отрезок, соединяющий две вершины, не лежащие на одной стороне четырехугольника. Таким образом, у любого четырехугольника может быть две диагонали: одна, соединяющая вершины, противоположные по сторонам, и другая – соединяющая вершины, поставленные по углам.
Доказательство взаимной перпендикулярности диагоналей в основном основывается на свойствах четырехугольника и его сторон. Ключевым моментом является нахождение параллельных сторон в данном многоугольнике, а также использование достаточных усовершенствований и геометрических теорем.
Доказательство взаимной перпендикулярности диагоналей в четырехугольнике

Дано: Четырехугольник ABCD.
Доказательство: 1. Проведем диагонали AC и BD. 2. Найдем углы ABC и BCD, используя соответствующие теоремы (например, теорему о сумме углов треугольника или теорему о внешнем угле треугольника). 3. Проверим, являются ли углы ABC и BCD прямыми. 4. Если углы ABC и BCD являются прямыми, то диагонали AC и BD взаимно перпендикулярны. 5. Если углы ABC и BCD не являются прямыми, то диагонали AC и BD не взаимно перпендикулярны. | Пример: |
Таким образом, доказательство взаимной перпендикулярности диагоналей в четырехугольнике заключается в проведении диагоналей, нахождении углов и проверке их прямизны.
Геометрия четырехугольников и их свойства

Существуют различные типы четырехугольников, включая выпуклые, невыпуклые, вписанные и описанные четырехугольники. Выпуклый четырехугольник имеет все углы меньше 180 градусов и все вершины направлены вовнутрь. Невыпуклый четырехугольник имеет хотя бы один угол больше 180 градусов или вершину, направленную внутрь. Вписанный четырехугольник описывается таким образом, что все его вершины лежат на окружности. Описанный четырехугольник описывается таким образом, что все вершины лежат на окружности, и сам четырехугольник полностью содержится внутри этой окружности.
Свойства четырехугольников:
- Сумма внутренних углов: сумма внутренних углов любого четырехугольника равна 360 градусов.
- Сумма длин сторон: сумма длин всех сторон четырехугольника определяет его периметр.
- Площадь: площадь четырехугольника может быть вычислена с использованием различных методов, включая формулу Герона для выпуклых четырехугольников или разбиение невыпуклых четырехугольников на треугольники.
- Диагонали: диагонали четырехугольника - отрезки, соединяющие его противоположные вершины. В некоторых четырехугольниках (например, квадрат или ромб) диагонали могут быть перпендикулярными, а в других четырехугольниках - нет.
Доказательство взаимной перпендикулярности диагоналей четырехугольника требует использования свойств углов и сторон. Существуют различные методы и геометрические теоремы, которые могут быть применены к доказательству перпендикулярности диагоналей в различных типах четырехугольников.
Способы доказательства перпендикулярности диагоналей
1. Использование теоремы о серединах отрезков:
Воспользуемся теоремой о серединах отрезков: если точка D - середина отрезка AC, то AD = DC. Рассмотрим четырехугольник ABCD с диагоналями AC и BD. Пусть точка E - середина диагонали AC. Тогда, согласно теореме о серединах отрезков, AE = EC. Рассмотрим теперь треугольник AEB. У него две стороны, равные сторонам треугольника CEB, а третья общая - диагональ AB. Но если в двух треугольниках две стороны равны, то третьи стороны также равны. Значит, AB = CE. Аналогичными рассуждениями можно показать, что AD = CD. Получаем, что AE = EC и AB = CE, значит, треугольники AEB и CEB равны по двум сторонам и по общей стороне. Следовательно, угол ABE равен углу CBE. Но это значит, что диагонали AC и BD перпендикулярны.
2. Использование теоремы о вписанных углах:
Рассмотрим четырехугольник ABCD с диагоналями AC и BD. Пусть угол ACB висячий. Тогда угол ADB - вписанный. Согласно теореме о вписанных углах в окружности, центральный угол BOC, соответствующий вписанному углу ADB, дает два различных дуги на окружности, равные углу ADB. Заметим, что эти дуги являются отрезками диагонали AC. Если угол ADB равен 90 градусам, то эти дуги будут полными окружностями, а следовательно, диагонали AC и BD будут перпендикулярны. Если угол ADB не равен 90 градусам, то эти дуги будут меньше половины окружности, но все равно будут представлять собой путь, который пройдет диагональ AC на окружности. Значит, найдется другая диагональ, пересекающая этот путь и перпендикулярная диагонали AC.
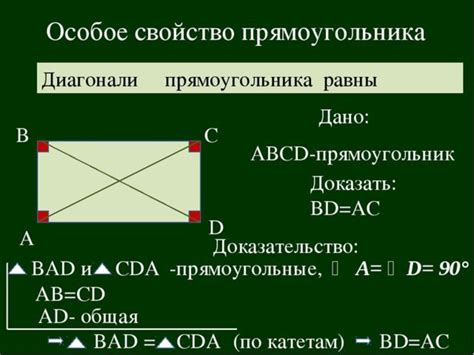
3. Использование свойств прямоугольников:
Рассмотрим четырехугольник ABCD с диагоналями AC и BD. Пусть ABCD - прямоугольник с углами B и D прямыми. Тогда, согласно свойствам прямоугольников, диагонали AC и BD перпендикулярны. Это можно доказать, например, рассмотрев две прямоугольные треугольники ABC и ADC и заметив, что углы ABC и ADC являются прямыми, а сторона AB прямо противоположна стороне AD.
Обратите внимание, что эти способы доказательства подходят для различных типов четырехугольников и могут использоваться совместно.
Описание доказательства взаимной перпендикулярности диагоналей четырехугольника
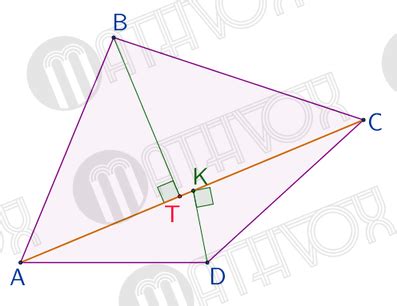
Чтобы доказать взаимную перпендикулярность диагоналей четырехугольника, необходимо воспользоваться свойствами геометрических фигур и треугольников. Предположим, что у нас есть четырехугольник ABCD с диагоналями AC и BD.
Во-первых, заметим, что диагонали делятся точкой пересечения M на две равные части. То есть, AM = CM и BM = DM.
Также, если мы проведем отрезки AB, BC, CD и DA, то получим четыре треугольника: ABC, BCD, CDA и DAB.
Доказательство основано на следующем рассуждении: если у нас есть два треугольника, в которых одна сторона и два прилежащих к ней угла равны соответственно другой стороне и двум углам другого треугольника, то эти треугольники равны.
В нашем случае, рассмотрим треугольники ABC и CDA. Мы можем утверждать, что сторона AB равна стороне CD (по условию) и углы ABC и CDA равны (перпендикулярность диагоналей). Следовательно, по приведенному ранее рассуждению, треугольники ABC и CDA равны.
Аналогично, рассмотрим треугольники BCD и DAB. Сторона BC равна стороне DA (по условию) и углы BCD и DAB равны (перпендикулярность диагоналей). Таким образом, треугольники BCD и DAB также равны.
Из равенства треугольников следует, что AM = CM и BM = DM (так как сторона AC равна стороне BD и углы ABC и CDA, BCD и DAB равны).
Таким образом, мы доказали, что диагонали AC и BD четырехугольника ABCD перпендикулярны друг другу.
Примеры применения доказательства в практике

1. Конструкция пересечения диагоналей: Доказав взаимную перпендикулярность диагоналей четырехугольника, мы можем использовать это свойство для построения точки их пересечения. Например, если у нас есть выпуклый четырехугольник ABCD, мы можем доказать, что его диагонали AC и BD перпендикулярны и затем использовать эту информацию для построения точки пересечения O. Это может быть полезно при решении задач на построение геометрических фигур.
2. Доказательство свойств параллелограмма: Если четырехугольник имеет параллельные стороны, то доказательство взаимной перпендикулярности его диагоналей может помочь нам доказать, что это параллелограмм. Например, если мы имеем параллелограмм ABCD с параллельными сторонами AB и CD, то доказательство перпендикулярности его диагоналей (AC и BD) может быть использовано для подтверждения, что он действительно является параллелограммом.
3 Лемма, связанная с правильными многоугольниками: В случае правильных многоугольников, взаимная перпендикулярность диагоналей может помочь в доказательстве определенных свойств. Например, если у нас есть правильный пятиугольник ABCDE, доказательство перпендикулярности его диагоналей (AC и BD) может помочь нам подтвердить, что каждый угол, образованный диагональю и стороной, равен 72 градусам. Это может быть полезно при решении задач на нахождение углов правильных многоугольников.
Таким образом, доказательство взаимной перпендикулярности диагоналей четырехугольника имеет широкие применения в геометрии и может быть полезным инструментом при работе с различными задачами и свойствами фигур.




