Одним из важных понятий в математическом анализе является предел функции. Предел позволяет определить поведение функции вблизи определенной точки. Но что делать, если функция не имеет предела? Как это доказать? В данной статье мы разберемся, как доказать отсутствие предела у функции.
Для начала, давайте вспомним, что такое предел функции. Предел функции f(x) при x, стремящемся к a, обозначается как lim(x -> a) f(x) и определяется следующим образом: если для любого положительного числа ε существует такое число δ > 0, что для всех x из интервала (a - δ, a + δ), отличных от a, выполняется неравенство |f(x) - L|
Следует отметить, что предельное значение может быть конечным числом, бесконечным числом или вовсе не существовать. Если функция не имеет предела, то говорят, что предел функции не существует (обозначается как lim(x -> a) f(x) = ∞ или lim(x -> a) f(x) = -∞). Теперь возникает вопрос: как доказать отсутствие предела у функции?
Понятие функции

Одна из основных характеристик функции – ее график, который представляет собой множество всех точек, образующихся в результате отображения значения аргументов на значения функции. Каждая точка графика имеет координаты (x, f(x)), где x – значение аргумента, f(x) – значение функции.
Функция может быть представлена различными способами, например, аналитически, графически, таблицей значений или в виде формулы.
Пример:
Рассмотрим функцию f(x) = 2x + 3. Пусть x принимает значения от 1 до 5 включительно.
- Подставим x = 1: f(1) = 2*1 + 3 = 2 + 3 = 5
- Подставим x = 2: f(2) = 2*2 + 3 = 4 + 3 = 7
- Подставим x = 3: f(3) = 2*3 + 3 = 6 + 3 = 9
- Подставим x = 4: f(4) = 2*4 + 3 = 8 + 3 = 11
- Подставим x = 5: f(5) = 2*5 + 3 = 10 + 3 = 13
Таким образом, значения функции для каждого значения аргумента определены, и мы можем построить ее график, который будет прямой линией с наклоном 2 и сдвигом вверх на 3 единицы.
Что такое предел функции
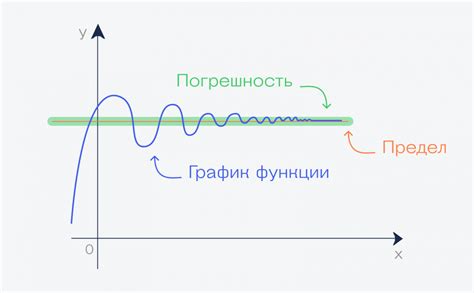
Математически, предел функции f(x) при x, стремящемся к a, равен L, если для любой заданной окрестности L можно указать окрестность a, такую, что для всех точек x, принадлежащих этой окрестности, значение f(x) будет близким к L.
Предел функции может быть равен конечному числу, плюс или минус бесконечности, или не существовать вовсе. Для определения предела функции часто используется формальное определение через эпсилон-дельта, а также свойства пределов функций и арифметические операции над пределами.
Предел функции играет важную роль в анализе и дифференциальном исчислении, помогая определить производные, непрерывность функции, а также исследовать границы их поведения в различных точках.
| Символ | Название | Определение |
|---|---|---|
| L | Предел функции | Значение, к которому стремится функция при стремлении аргумента к определенной точке |
| a | Точка предела | Точка, к которой стремится аргумент функции |
Критерии отсутствия предела

Отсутствие предела у функции можно доказать, используя различные критерии. Вот несколько из них:
1. Критерий Гейне. Если для любой последовательности значений аргумента, стремящейся к некоторому предельному значению, существует такое подпоследовательность значений функции, которая не имеет предела, то говорят, что у функции отсутствует предел.
2. Критерий Коши. Функция не имеет предела в точке, если для любой сколь угодно малой величины $\varepsilon > 0$ существует такое положительное число $\delta > 0$, что для любого значения $x$ из проколотого $\delta$-окрестности точки $a$ выполняется условие $|f(x)-l|\ge \varepsilon$, где $l$ - некоторое число.
3. Критерий Коши для последовательностей. Если для любой последовательности значений $x_n}$, сходящейся к точке $a$, существует такая малая величина $\varepsilon > 0$, что для любого номера $N$ найдется номер $n>N$, для которого $)-l|\ge\varepsilon$, где $l$ - некоторое число, то говорят, что у функции отсутствует предел.
4. Критерий Коши для функций. Функция $f(x)$ не имеет предела в точке $a$, если для любой сколь угодно малой величины $\varepsilon > 0$ найдется такая малая величина $\delta > 0$, что для любых значений $x$ и $y$, лежащих в интервале $(a-\delta, a+\delta)$, выполняется неравенство $|f(x)-f(y)|\ge \varepsilon$.
Использование этих критериев позволяет доказывать отсутствие предела у функции и устанавливать его недостаточность в определенных точках.
Методы доказательства

Для доказательства отсутствия предела у функции существует несколько методов:
1. Метод последовательностей - заключается в нахождении двух последовательностей из множества значений функции, сходящихся к разным пределам. Если такие последовательности существуют, то предел функции не существует.
2. Метод производных - основан на анализе производных функции. Если производная неограничена или имеет разные пределы в различных точках, то предел функции не существует.
3. Метод окрестностей - предполагает нахождение двух окрестностей точки, в которых функция принимает значения, сходящиеся к разным пределам. Если такие окрестности существуют, то предел функции не существует.
4. Метод отрицания определения - заключается в применении непосредственно определения предела функции и поиске контрпримера. Если найдется хотя бы один контрпример, то предел функции не существует.
Каждый из этих методов имеет свои преимущества и недостатки. Также следует помнить о том, что некоторые функции имеют особенности, при которых их предел может не существовать.
Связь между пределом и разрывом функции

Интересно отметить, что связь между пределом и разрывом функции может быть очень тесной. Разрыв функции возникает, когда функция не принимает одно или несколько значений в некоторой точке. Это может происходить по разным причинам, например, когда функция имеет точку разрыва, точку устранимого разрыва или точку разрыва первого рода.
Если функция имеет предел в точке, то она может быть непрерывна в данной точке или иметь устранимый разрыв. Непрерывная функция не имеет разрывов и может быть нарисована без снятия карандаша с бумаги, в то время как функция с устранимым разрывом может иметь точку разрыва, но предел в данной точке существует.
С другой стороны, если функция не имеет предела в некоторой точке, это может указывать на разрыв функции. Например, функция может иметь разрыв первого рода, когда пределы с левой и правой стороны существуют, но не равны друг другу. Также возможен разрыв второго рода, когда пределы с левой и правой стороны не существуют или равны бесконечности.
Таким образом, анализ пределов функции позволяет нам получить информацию о разрывах функции, а анализ разрывов функции может помочь нам понять, есть ли предел функции в данной точке. Эти два концепта взаимосвязаны и важны для понимания поведения функций в математическом анализе.
Примеры функций без предела
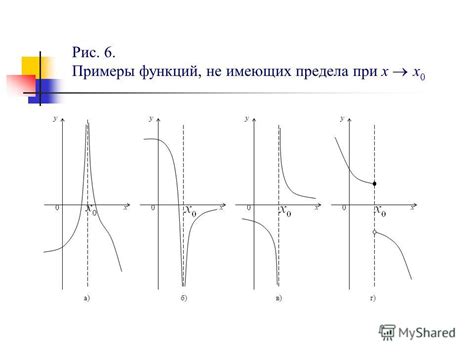
1. Функция скачкообразного роста:
Рассмотрим функцию $f(x) = \left\{
\begin{array}{ll}
1, & x \leq 0 \\
0, & x > 0
\end{array}
ight.$
В данном случае у функции нет предела в точке $x = 0$, так как значения функции не стремятся к какому-либо конкретному числу при приближении к нулю справа или слева.
2. Функция с бесконечным возрастанием:
Рассмотрим функцию $f(x) = \frac{1}{x}$.
При $x$ стремящемся к нулю, значение функции стремится к бесконечности. Таким образом, предела у данной функции нет в точке $x = 0$.
3. Функция с осцилляцией:
Рассмотрим функцию $f(x) = \sin\left(\frac{1}{x}
ight)$.
Данная функция осциллирует бесконечное число раз при приближении к нулю. Также значение функции не стремится к какому-либо конкретному числу, следовательно, предела у данной функции нет в точке $x = 0$.
Особые случаи отсутствия предела

Существует несколько особых случаев, когда функция не имеет предела:
| Случай | Описание |
|---|---|
| Бесконечный рост | Если функция стремится к бесконечности при приближении аргумента к некоторому значению, то предел не существует. Например, функция f(x) = x^2 не имеет предела при x стремящемся к плюс бесконечности, так как функция продолжает расти. |
| Бесконечные колебания | Если функция периодически меняет значение между положительными и отрицательными значениями, то предел также не существует. Например, функция f(x) = sin(x) не имеет предела при x стремящемся к плюс или минус бесконечности, так как значение функции колеблется между -1 и 1. |
| Разрывы | Если функция имеет точки разрыва или различные значения функции при приближении аргумента с разных сторон, то предел также не существует. Например, функция f(x) = 1/x не имеет предела при x стремящемся к нулю, так как значение функции становится бесконечно большим при приближении справа и бесконечно малым при приближении слева к нулю. |
В этих случаях для определения поведения функции можно использовать другие методы, например, анализ производных или изучение экстремальных точек.



