Подобие треугольников - одно из основных понятий геометрии. По сути, подобие означает, что две фигуры имеют одинаковые углы и пропорциональные стороны. В данной статье мы рассмотрим как доказать подобие треугольников в трапеции, то есть, как установить, что два треугольника, образованные внутри трапеции, подобны.
Для начала, давайте вспомним, что такое трапеция. Трапеция - это четырехугольник, у которого хотя бы две стороны параллельны. Одна из параллельных сторон называется основанием, а другая - боковой стороной. Также в трапеции есть два боковых угла и два основных угла.
Чтобы доказать подобие треугольников в трапеции, мы можем использовать несколько подходов. Один из них - использование свойства углов треугольника. Если в трапеции мы можем найти два треугольника с одинаковыми углами, то они будут подобны. Другой подход - использование свойства пропорциональности сторон. Если мы можем установить, что соотношение длин сторон в двух треугольниках одинаково, то они также будут подобны.
Что такое подобие треугольников

Подобие треугольников позволяет нам узнать много полезной информации о геометрических фигурах и решать различные задачи. Например, если мы знаем, что два треугольника подобны, то можем вычислить отношение их сторон и углов, а также найти длины сторон и площади.
Подобие треугольников имеет несколько важных свойств:
- Углы подобных треугольников равны. Это означает, что соответствующие углы одного треугольника равны соответствующим углам другого треугольника.
- Стороны подобных треугольников пропорциональны. Это означает, что отношение длин соответствующих сторон одного треугольника к длинам соответствующих сторон другого треугольника является постоянным числом.
- Подобные треугольники имеют одинаковые формы, но могут отличаться размерами. То есть один треугольник можно получить из другого путем изменения размеров.
Подобие треугольников является основой для понимания и решения сложных задач в геометрии. Оно позволяет нам использовать знания о подобии треугольников для нахождения неизвестных величин и доказательства различных свойств и теорем. Подобие треугольников также находит свое применение в различных областях науки и техники, включая архитектуру, инженерию и физику.
Методы доказательства

Существуют несколько методов доказательства подобия треугольников в трапеции:
- Соответствие углов: Если два треугольника имеют соответствующие равные углы, то они подобны.
- Соответствие сторон: Если отношение длин соответствующих сторон двух треугольников одинаково, то они подобны.
- Сочетание углов и сторон: Используя как соответствие углов, так и соответствие сторон, можно доказать подобие треугольников в трапеции.
Для применения методов доказательства подобия треугольников в трапеции часто используют свойства треугольников, такие как равенство суммы углов треугольника 180 градусов, свойства параллельных и перпендикулярных прямых и др.
Выбор конкретного метода доказательства зависит от условий и формулировки задачи, поэтому в каждом конкретном случае нужно анализировать и применять подходящий метод и свойства треугольников.
Основные признаки подобия треугольников
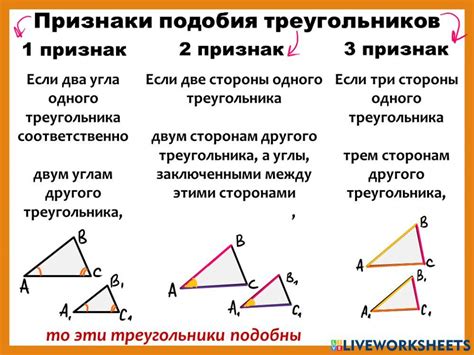
1. Угловой признак: Если два треугольника имеют два угла, равных между собой, то эти треугольники подобны.
2. Признак равенства соответствующих углов: Если два треугольника имеют все три угла, равных соответственно друг другу, то эти треугольники подобны.
3. Признак равенства всех углов и соответствующих сторон: Если два треугольника имеют все три угла, равных соответственно друг другу, и все соответствующие стороны пропорциональны, то эти треугольники подобны.
4. Признак равенства двух углов и соответствующих сторон: Если два треугольника имеют два угла, равных соответственно друг другу, и две стороны, пропорциональные этим углам, то эти треугольники подобны.
5. Признак равенства трех сторон: Если два треугольника имеют все три стороны, пропорциональные соответственно друг другу, то эти треугольники подобны.
Признаки подобия треугольников помогают установить соотношение между соответствующими сторонами и углами треугольников, что является важным инструментом для решения различных геометрических задач.
Доказательство подобия треугольников в трапеции

В трапеции существуют две пары подобных треугольников: основания с боковыми сторонами и диагонали с основаниями.
Чтобы доказать подобие треугольников в трапеции, мы должны использовать свойства и законы геометрии.
- Диагонали трапеции:
- Углы оснований:
- Боковые стороны:
- Диагонали с основаниями:
Рассмотрим трапецию ABCD с диагоналями AC и BD.
Углы ACB и ADB являются соответственными углами, так как они лежат на прямых AD и CB и на разных сторонах от пересекающей их прямой BD. Поэтому углы ACB и ADB равны.
Основания трапеции (AB и CD) и боковые стороны (BC и AD) имеют общий угол при основании. Кроме того, стороны BC и AD являются параллельными, так как они являются боковыми сторонами трапеции. Таким образом, треугольники ABC и DAD подобны по стороне-уголу.
Диагонали AC и BD пересекаются в точке E. Треугольник ABE и CDE имеют общий угол при основании, так как лежат на прямых BE и DE и на разных сторонах от пересекающей их прямой AC. Кроме того, стороны AE и CE являются параллельными, так как они являются диагоналями трапеции. Следовательно, треугольники ABE и CDE подобны по стороне-уголу.
Таким образом, мы доказали подобие треугольников в трапеции ABCD: треугольники ABC и DAD, а также треугольники ABE и CDE.
Примеры доказательства
Доказательство подобия треугольников в трапеции может быть выполнено с использованием различных методов и свойств треугольников.
Один из примеров доказательства основан на свойстве параллельных линий и соответствующих углах:
Рассмотрим треугольник ABC и треугольник ADE, где точка D - середина стороны AB, а точка E - точка на стороне BC такая, что DE



