Тетраэдр – это одна из наиболее знаменитых геометрических фигур в трехмерном пространстве. Его основные характеристики – это равные боковые грани и углы между ними. Доказать, что тетраэдр правильный, можно разными способами, например, через координаты его вершин.
Для начала, необходимо знать, что тетраэдр состоит из четырех вершин, которые образуют четыре треугольника. Радиус вписанной сферы тетраэдра проходит через его вершины, а высота каждого треугольника проходит через его основание и перпендикулярна этой основе.
Если известны координаты вершин тетраэдра, то можно проверить, является ли каждая его грань равносторонним треугольником. Для этого необходимо вычислить расстояние между каждой из вершин и найти длину всех сторон треугольника, образованного этими вершинами. Если все стороны треугольника равны, то тетраэдр будет правильным.
Алгоритм доказательства правильности тетраэдра через координаты
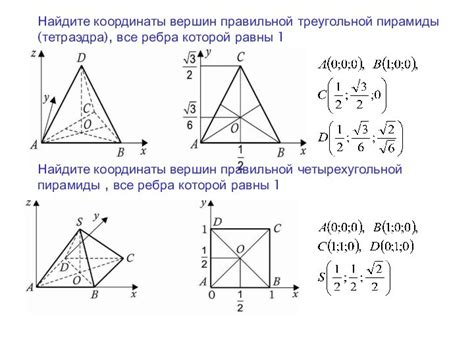
Доказательство правильности тетраэдра можно осуществить с использованием координатных вычислений. Для этого необходимо выполнить следующие шаги:
- Выберите систему координат.
- Запишите координаты вершин тетраэдра.
- Вычислите длины сторон.
- Проверьте, что все стороны тетраэдра равны друг другу.
- Вычислите длины диагоналей.
- Проверьте, что все диагонали тетраэдра равны друг другу.
- Проверьте, что все углы тетраэдра равны друг другу.
Для того чтобы сравнить длины сторон и диагоналей, можно использовать формулу расстояния между двумя точками в трехмерном пространстве:
$$d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}.$$
Если после выполнения всех шагов окажется, что все стороны и диагонали равны, а также все углы тетраэдра равны между собой, то можно сделать заключение о том, что тетраэдр правильный.
Приведенный алгоритм позволяет доказать правильность тетраэдра с помощью координатных вычислений. Он является надежным и математически обоснованным способом определения правильности этой геометрической фигуры.
Определение координат вершин тетраэдра
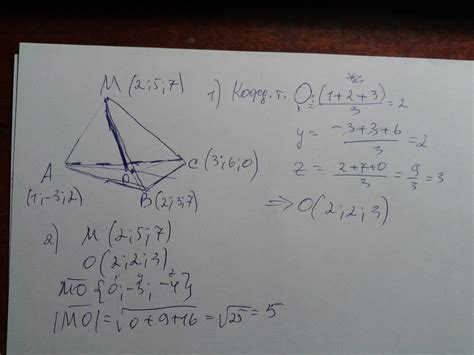
Предположим, что тетраэдр имеет вершины A, B, C и D. Для определения координат каждой вершины необходимо провести следующие шаги:
1. Задать систему координат. Определить оси OX, OY и OZ, чтобы они были перпендикулярны друг другу.
2. Определить координаты вершины A. Выберите любую точку в пространстве и назовите ее A. Запишите ее координаты (xA, yA, zA).
3. Найти координаты вершины B. Расстояние от вершины B до вершины A должно быть равно длине ребра AB в правильном тетраэдре. Используйте формулы для вычисления расстояния между двумя точками в трехмерном пространстве, чтобы найти координаты вершины B.
4. Определить координаты вершины C. Расстояние от вершины C до вершины A должно быть равно длине ребра AC в правильном тетраэдре. Используйте формулы для вычисления расстояния между двуми точками в трехмерном пространстве, чтобы найти координаты вершины C.
5. Найти координаты вершины D. Расстояние от вершины D до вершины A должно быть равно длине ребра AD в правильном тетраэдре. Используйте формулы для вычисления расстояния между двумя точками в трехмерном пространстве, чтобы найти координаты вершины D.
Можно использовать дополнительные формулы и связи между координатами вершин тетраэдра для более простого нахождения координат.
Расчет длин сторон тетраэдра
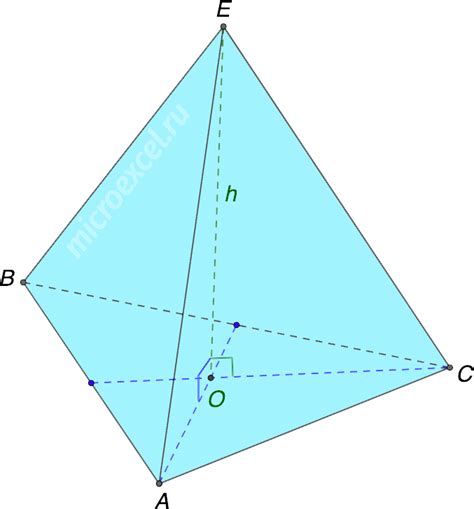
Предположим, что координаты вершин тетраэдра заданы следующим образом:
- Вершина A: (x1, y1, z1)
- Вершина B: (x2, y2, z2)
- Вершина C: (x3, y3, z3)
- Вершина D: (x4, y4, z4)
Длины сторон тетраэдра могут быть вычислены с помощью следующих формул:
- Сторона AB: √((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2)
- Сторона AC: √((x3 - x1)2 + (y3 - y1)2 + (z3 - z1)2)
- Сторона AD: √((x4 - x1)2 + (y4 - y1)2 + (z4 - z1)2)
- Сторона BC: √((x3 - x2)2 + (y3 - y2)2 + (z3 - z2)2)
- Сторона BD: √((x4 - x2)2 + (y4 - y2)2 + (z4 - z2)2)
- Сторона CD: √((x4 - x3)2 + (y4 - y3)2 + (z4 - z3)2)
Если найденные значения длин всех сторон тетраэдра совпадают, то тетраэдр является правильным.
Проверка условий равенства сторон
Пусть у нас есть тетраэдр с вершинами A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) и D(x4, y4, z4).
Расстояние между любыми двумя вершинами тетраэдра можно вычислить с помощью формулы:
d = √((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2)
Необходимо проверить равенство всех сторон тетраэдра:
| AB: | dAB = √((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2) |
| AC: | dAC = √((x3-x1)^2 + (y3-y1)^2 + (z3-z1)^2) |
| AD: | dAD = √((x4-x1)^2 + (y4-y1)^2 + (z4-z1)^2) |
| BC: | dBC = √((x3-x2)^2 + (y3-y2)^2 + (z3-z2)^2) |
| BD: | dBD = √((x4-x2)^2 + (y4-y2)^2 + (z4-z2)^2) |
| CD: | dCD = √((x4-x3)^2 + (y4-y3)^2 + (z4-z3)^2) |
Если все стороны тетраэдра равны, то тетраэдр является правильным.
Проверка условий равенства углов
Для этого сначала найдем координаты вершин тетраэдра в пространстве. Пусть A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) и D(x4, y4, z4) - вершины тетраэдра.
Затем найдем векторы AB, AC и AD:
AB = B - A = (x2 - x1, y2 - y1, z2 - z1)
AC = C - A = (x3 - x1, y3 - y1, z3 - z1)
AD = D - A = (x4 - x1, y4 - y1, z4 - z1)
Далее вычислим скалярные произведения векторов AB, AC и AD:
AB · AC = (x2 - x1) * (x3 - x1) + (y2 - y1) * (y3 - y1) + (z2 - z1) * (z3 - z1)
AB · AD = (x2 - x1) * (x4 - x1) + (y2 - y1) * (y4 - y1) + (z2 - z1) * (z4 - z1)
AC · AD = (x3 - x1) * (x4 - x1) + (y3 - y1) * (y4 - y1) + (z3 - z1) * (z4 - z1)
Если полученные значения равны между собой, то углы между векторами AB, AC и AD равны. Такое равенство свидетельствует о правильности тетраэдра.
Итак, чтобы доказать, что тетраэдр является правильным, необходимо:
- Найти координаты всех его вершин.
- Найти векторы AB, AC и AD, используя найденные координаты.
- Вычислить скалярные произведения векторов AB, AC и AD.
- Сравнить полученные значения скалярных произведений. Если они равны между собой, то углы между векторами AB, AC и AD равны, что свидетельствует о правильности тетраэдра.



