Изучение геометрии начинается с базовых понятий, таких как равенство углов. Знание этого понятия позволяет нам доказывать различные свойства треугольников и других геометрических фигур. В этой статье мы рассмотрим несколько способов доказать равенство углов в треугольнике.
Первый способ основан на равенстве углов, образованных параллельными прямыми. Если в треугольнике имеются две параллельные стороны, то соответствующие им углы будут равны. Данное правило также применимо к дополнительным углам, образованным пересекающимися прямыми.
Второй способ заключается в использовании свойств треугольника. Например, в равнобедренном треугольнике боковые стороны равны, а значит, их прилежащие углы также будут равны. Также, в прямоугольном треугольнике угол, противолежащий гипотенузе, будет равен сумме двух других углов.
Что такое равные углы?
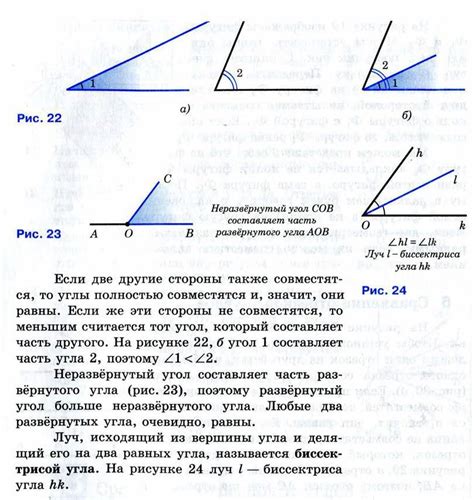
Равные углы могут быть определены по различным свойствам и признакам:
- Углы, которые расположены на одной стороне от пересекающей прямой и имеют одинаковую меру, являются равными углами.
- Углы, которые лежат на параллельных прямых и пересекаются третьей прямой, считаются равными углами. Это известно как углы-параллельники, и они имеют равные меры между собой.
- Углы, которые являются вершинными углами двух треугольников, считаются равными углами.
Равные углы важны при изучении геометрии, особенно в треугольниках. Они помогают нам анализировать и доказывать различные свойства треугольников, такие как равные стороны и пропорциональные углы. Знание о равных углах поможет вам решать задачи и улучшить ваше понимание геометрии в целом.
Помните, что для демонстрации равных углов нужно обращать внимание на их меру и расположение в отношении других углов и прямых.
Методы доказательства

Существует несколько методов, которые могут быть использованы для доказательства равенства углов в треугольниках:
1. Метод двух углов: Если два угла в одном треугольнике равны двум углам в другом треугольнике, то третьи углы обоих треугольников также равны. Доказательство основано на свойстве суммы углов треугольника.
2. Метод сторон и углов: Если два треугольника имеют равные стороны и равные углы между ними, то они равны по всему треугольнику. Доказательство основано на свойствах равных треугольников.
3. Метод параллельных прямых: Если две параллельные прямые пересекаются третьей прямой, то соответствующие углы, образуемые при пересечении, равны. Доказательство основано на свойствах параллельных линий и секущей.
4. Метод вписанных углов: Если два треугольника имеют равные вписанные углы на одной дуге окружности, то они равны по всему треугольнику. Доказательство основано на свойствах вписанных углов и дуг окружности.
5. Метод равенства длин отрезков: Если два треугольника имеют равные длины отрезков, то они равны по всему треугольнику. Доказательство основано на свойствах равных треугольников и равенства отрезков.
Важно помнить, что для доказательства равенства углов в треугольниках необходимо использовать несколько фактов и методов одновременно. Только с помощью одного метода, часто, не удастся достичь желаемого доказательства.
Метод угловых наклонений
Для применения метода угловых наклонений необходимо знать следующие основные факты:
| 1. Углы при основании равнобедренного треугольника равны. |
| 2. В сумме углы треугольника равны 180 градусов. |
| 3. Углы, образованные параллельными прямыми, их пересекающими и третьей прямой, называемой трансверсалью, также равны. |
Используя эти факты, можно доказать равенство углов в треугольнике с помощью метода угловых наклонений:
1. Для начала, рассмотрим треугольник и выделим два его непересекающихся угла.
2. Найдем прямую, пересекающую сторону треугольника и образующую внешний угол с одним из непересекающихся углов.
3. С помощью факта 3 можно заметить, что этот внешний угол равен сумме двух углов прилежащих сторон.
4. Сравним эту сумму с другим непересекающимся углом и проверим их равенство, используя факты 1 и 2.
Если оба угла равны, то равенство углов в треугольнике доказано с помощью метода угловых наклонений.
Метод сегментов
Для применения метода сегментов необходимо иметь треугольник и знать некоторые его характеристики, такие как длины сторон, заданные углы или параллельные прямые.
Чтобы доказать равенство углов с помощью метода сегментов, следует последовательно выполнять следующие шаги:
- Найти все смежные углы, которые можно использовать в доказательстве.
- Построить отрезок или отрезки, которые пересекают прямые, содержащие данные углы.
- Использовать свойства смежных и вертикальных углов для нахождения равенства углов.
Например, требуется доказать, что угол А и угол В в треугольнике ABC равны. Мы знаем, что прямая BD параллельна прямой AC. Отрезок BE пересекает эти прямые, образуя вертикальные углы ABE и CBD. Исходя из свойств вертикальных углов, мы можем заключить, что угол А и угол В равны.
Таким образом, метод сегментов позволяет эффективно доказывать равенство углов в треугольнике, используя свойства параллельных и пересекающихся прямых, а также свойства смежных и вертикальных углов.
Метод параллельных линий
Метод параллельных линий основан на теореме о параллельных прямых и позволяет доказать равенство углов в треугольнике. Для применения этого метода необходимо иметь треугольник и две параллельные линии, каждая из которых пересекает стороны треугольника.
Процесс доказательства равенства углов с использованием метода параллельных линий состоит из следующих шагов:
- Нарисуйте треугольник ABC и отметьте его стороны.
- Возьмите параллельную линию, которая пересекает сторону AB.
- Обозначьте точку пересечения линии с стороной AB как D.
- Возьмите вторую параллельную линию, которая пересекает сторону AC.
- Обозначьте точку пересечения второй линии с стороной AC как E.
- Возьмите третью линию, которая соединяет точки D и E.
- Обозначьте точку пересечения третьей линии с стороной BC как F.
- Докажите, что угол A равен углу F.
В результате выполнения этих шагов можно показать, что углы A и F равны. Таким образом, метод параллельных линий позволяет доказать равенство углов в треугольнике, используя параллельные линии и теорему о параллельных прямых.
 |  |
| Треугольник ABC | Параллельные линии |
Метод доказательства по теоремам

Для доказательства равенства углов в треугольнике можно использовать различные теоремы и свойства геометрии. В данном разделе рассмотрим несколько наиболее часто применяемых теорем.
1. Теорема о сумме углов треугольника: сумма всех углов треугольника равна 180 градусам. Если известны значения двух углов, то третий угол можно найти вычитанием суммы из 180 градусов.
| Угол 1 | Угол 2 | Угол 3 |
| значение | значение | 180 - (значение Угол 1 + значение Угол 2) |
2. Теорема об углах, дополнительных к одному углу: если у двух углов сумма равна 180 градусам, то эти углы называются дополнительными друг к другу.
| Угол 1 | Угол 2 | Угол 3 |
| значение | 180 - (значение Угол 1) | 180 - (значение Угол 2) |
3. Теорема о параллельных прямых и углах: если две прямые параллельны, то соответственные углы равны.
| Угол 1 | Угол 2 |
| значение | значение |
Свойства равных углов
Равные углы в треугольнике имеют несколько важных свойств:
- Если два угла треугольника равны, то их противоположные стороны также равны.
- Если две стороны треугольника равны, то их противоположные углы также равны.
- Если углы при основании равнобедренного треугольника равны, то основание треугольника является серединой между основаниями двух равных углов.
- Если угол при вершине равнобедренного треугольника равен углу между основанием и боковой стороной, то основание треугольника является отрезком, равноудаленным от основания двух равных углов.
Знание этих свойств позволяет нам доказывать равенства углов в треугольнике и успешно решать задачи, связанные с треугольниками.
Сумма равных углов
В треугольнике существуют различные свойства, которые позволяют доказать равенство углов. Одно из таких свойств заключается в том, что сумма равных углов равна 180 градусов.
Рассмотрим треугольник ABC. Предположим, что угол A и угол B равны. Обозначим эти углы как α. Сумма углов треугольника равна 180 градусов. Значит, угол C равен 180 - α градусов.
Теперь посмотрим на треугольник ACD. Это прямоугольный треугольник, у которого угол A равен углу C. Значит, угол D также равен α градусов.
Получается, что в треугольнике ABC с двумя равными углами α, сумма этих углов равна 180 градусов.
Углы при пересекающихся прямых
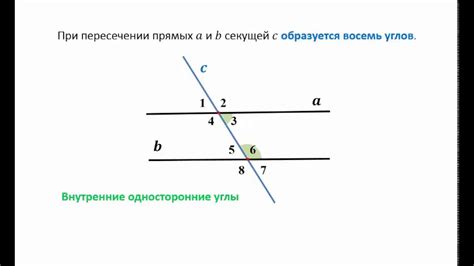
Когда две прямые пересекаются, образуется система углов, которая имеет определенные свойства. В данной статье мы рассмотрим основные правила равенства углов при пересекающихся прямых.
1. Вертикальные углы. Если две прямые пересекаются, то углы, образованные этими прямыми и параллельными прямыми, называются вертикальными углами. Вертикальные углы всегда равны друг другу.
Пример: В треугольнике ABC AC и BD - высоты. Углы В и D являются вертикальными углами, поэтому они равны: ∠B = ∠D.
2. Параллельные прямые. Если две прямые параллельны и пересекаются третьей прямой, то образуются соответственные углы, внутренние углы и внешние по две пары. Соответственные углы равны.
Пример: Прямые l₁ и l₂ параллельны и пересекаются прямой m. Угол a и угол b - соответственные углы, поэтому они равны: ∠a = ∠b.
3. Угол пересечения. Угол, образованный при пересечении двух прямых, называется углом пересечения. Углы пересечения, лежащие по одну сторону от пересекающей прямой, но на разных прямых, называются смежными недополнительными углами и всегда равны друг другу.
Пример: Прямые p и q пересекаются прямой l. Углы a и b являются смежными углами, поэтому они равны: ∠a = ∠b.
Зная эти основные правила равенства углов при пересекающихся прямых, можно доказывать много различных утверждений и свойств в геометрии.
Необходимо помнить, что равенство углов в треугольнике имеет свои особенности и правила, которые следует учитывать при решении геометрических задач.



