Изучение плоскостей и их взаимного расположения в пространстве является важной задачей в геометрии. При анализе объектов, ограниченных плоскостями, в некоторых случаях необходимо доказать, что плоскость проходит через заданную вершину. Для этого существуют определенные методы и подходы.
Один из подходов, который можно использовать, основан на свойствах плоскостей и прямых в пространстве. Во-первых, для доказательства того, что плоскость проходит через вершину, вам необходимо знать координаты этой вершины и уравнение плоскости. После этого вы можете подставить координаты вершины в уравнение плоскости и убедиться, что полученное равенство выполняется. Если оно выполняется, то это означает, что плоскость проходит через заданную вершину.
Однако, если у вас есть только две точки на плоскости и задача состоит в том, чтобы доказать, что плоскость проходит через вершину, можно воспользоваться следующим методом. Пусть у вас есть две точки на плоскости - это точка А и точка В. Сначала вычислите вектор, имеющий начало в точке А и конец в точке В. Затем найдите вектор, имеющий начало в точке А и параллельный заданной плоскости. Если эти два вектора равны или коллинеарны, то это означает, что плоскость проходит через вершину (точку А), так как вектор, параллельный плоскости, будет иметь такое же направление, что и вектор, идущий от точки А до точки В.
Методы доказательства прохождения плоскости через вершину
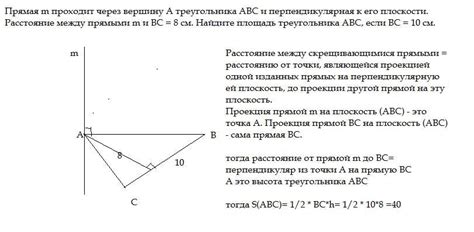
Существуют различные методы, которые позволяют доказать прохождение плоскости через вершину. Рассмотрим некоторые из них:
| Метод | Описание |
|---|---|
| Метод координат | |
| Метод направляющих векторов | |
| Метод перпендикулярности | Этот метод основан на свойстве перпендикулярности плоскости к прямым, лежащим на ней. Для доказательства прохождения плоскости через вершину необходимо показать, что прямая, проходящая через данную вершину, перпендикулярна плоскости. |
Выбор конкретного метода зависит от условий задачи и предпочтений исследователя. Важно помнить, что доказательство прохождения плоскости через вершину требует строгости и точности в рассуждениях и использовании математических инструментов.
Использование координатной системы для доказательства
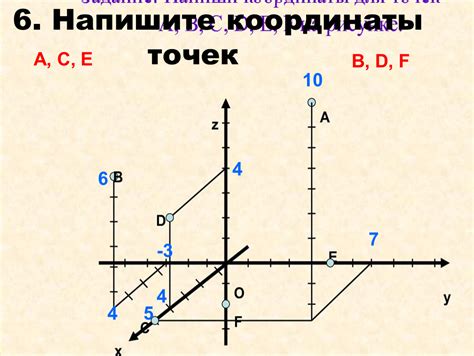
Координатная система предоставляет удобный способ доказать, что плоскость проходит через вершину. Для этого необходимо выполнить следующие шаги:
Шаг 1: Выберите систему координат, которая соответствует задаче. Начало координат обычно выбирается в вершине, через которую должна проходить плоскость.
Шаг 2: Запишите уравнение плоскости в общем виде, используя координаты точек, через которые она должна проходить. Обычно это уравнение имеет вид: ax + by + cz + d = 0, где a, b, c и d - коэффициенты, а x, y и z - координаты точек. Например, если плоскость должна проходить через точки (1, 2, 3) и (4, 5, 6), то уравнение будет иметь вид: a(1) + b(2) + c(3) + d = 0 и a(4) + b(5) + c(6) + d = 0.
Шаг 3: Подставьте координаты вершины, через которую должна проходить плоскость, в уравнение плоскости. Если после подстановки значения равны, то это означает, что плоскость проходит через вершину. Например, если вершина имеет координаты (1, 2, 3), то уравнение будет иметь вид: a(1) + b(2) + c(3) + d = 0.
Шаг 4: Решите полученное уравнение для определения значений коэффициентов a, b, c и d. Например, если после подстановки координат вершины получилось уравнение: 2a + 4b + 6c + d = 0, то коэффициенты будут:
a = 2
b = -2
c = -2
d = 2.
Таким образом, использование координатной системы позволяет легко доказать, что плоскость проходит через вершину, выполнив все описанные шаги.
Установление геометрической связи между плоскостью и вершиной

Для доказательства того, что плоскость проходит через вершину, необходимо выполнить следующие шаги:
- Определить координаты вершины. В трехмерном пространстве вершина задается тройкой чисел (x, y, z), где x, y и z - координаты по осям x, y и z соответственно.
- Записать уравнение плоскости. Уравнение плоскости обычно записывается в виде Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты, а x, y и z - переменные.
- Подставить координаты вершины в уравнение плоскости. Если после подстановки все значения равны нулю, то это означает, что плоскость проходит через вершину.
Например, если у нас есть плоскость с уравнением 2x + 3y - z + 4 = 0, и вершина с координатами (1, -2, 3), то мы можем подставить эти значения в уравнение:
2(1) + 3(-2) - (3) + 4 = 0
2 - 6 - 3 + 4 = 0
-3 - 3 + 4 = 0
-6 + 4 = 0
-2 = 0
Поскольку последнее уравнение неверно, мы можем заключить, что плоскость не проходит через данную вершину.
Таким образом, установление геометрической связи между плоскостью и вершиной позволяет определить, проходит ли плоскость через данную вершину и использовать эту информацию для дальнейших анализов и построений.
Приведение уравнения плоскости к каноническому виду

Для доказательства того, что плоскость проходит через вершину, необходимо привести уравнение плоскости к каноническому виду.
Каноническое уравнение плоскости имеет следующий вид:
| А | х | + | В | у | + | С | z | + | D | = | 0 |
где A, B и C - коэффициенты перед переменными x, y и z, D - свободный член.
Чтобы привести уравнение плоскости к каноническому виду, нужно выполнить несколько шагов:
- Раскрыть скобки и собрать все одночлены с переменными x, y и z в одну часть уравнения, а свободные члены в другую.
- Разделить обе части уравнения на общий множитель перед переменными x, y и z.
После выполнения этих шагов, уравнение плоскости будет иметь канонический вид. Далее следует проверить, что координаты вершины, через которую должна проходить плоскость, удовлетворяют данному уравнению. Если они удовлетворяют, то это доказывает, что плоскость действительно проходит через вершину.
Проверка условий, определяющих прохождение плоскости через вершину
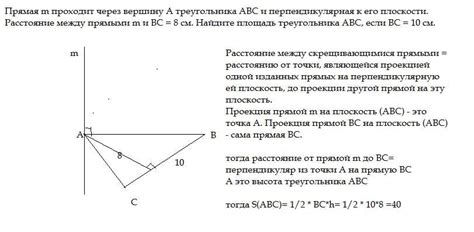
Для доказательства того, что плоскость проходит через вершину, необходимо проверить выполнение следующих условий:
- Найти координаты вершины плоскости. Это может быть начальная точка или другая известная точка на плоскости.
- Подставить координаты вершины плоскости в уравнение плоскости и убедиться, что оно выполняется. Уравнение плоскости обычно записывается в виде Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты плоскости.
Эти условия являются необходимыми и достаточными для доказательства прохождения плоскости через вершину. Если они выполняются, то можно с уверенностью утверждать, что плоскость проходит через данную точку.
Использование свойств симметрии для доказательства
Для начала, определим плоскость, проходящую через вершину. Затем, с использованием свойств симметрии, покажем, что другие точки находятся на одинаковом расстоянии от этой плоскости.
Одно из основных свойств симметрии, которое можно использовать в данном случае, называется плоскостной симметрией. Оно утверждает, что если точка А находится на одинаковом расстоянии от плоскостей А1 и А2, то плоскости А1 и А2 тоже проходят через эту точку.
Допустим, у нас есть плоскость А1, проходящая через вершину, и точка В, которая также находится на равном расстоянии от этой плоскости. Мы также знаем, что плоскость А1 и плоскость, проходящая через вершину, пересекаются. Следовательно, используя свойство плоскостной симметрии, мы можем заключить, что плоскость, проходящая через вершину, также проходит через точку В.
Другим свойством, которое мы можем использовать, называется осевой симметрией. Оно говорит о том, что если точка G является центром симметрии между точками А и В, и плоскость А2 проходит через А, то она также проходит через точку G. В данном случае, точка А - это вершина, точка В - это точка, принадлежащая плоскости, проходящей через вершину, и точка G - это точка, находящаяся на одинаковом расстоянии от точек А и В.
Используя свойства симметрии, мы можем доказать, что плоскость проходит через вершину, показывая, что другие точки находятся на одинаковом расстоянии от этой плоскости. Этот метод доказательства основан на математических принципах и позволяет нам установить связь между вершиной и плоскостью.
Анализ взаимного расположения плоскости и вершины в пространстве
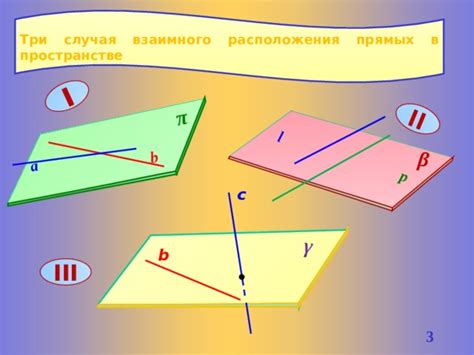
- Задать уравнение плоскости в пространстве. Для этого необходимо иметь информацию о координатах трех (или более) точек, лежащих на плоскости.
- Подставить координаты вершины в уравнение плоскости. Если после подстановки получаем верное равенство, то плоскость проходит через данную вершину.
- Если после подстановки координат вершины в уравнение плоскости получаем неверное равенство, то плоскость не проходит через данную вершину. В этом случае можно провести дополнительные исследования, например, проверить взаимное расположение других точек на плоскости и в пространстве.
При анализе взаимного расположения плоскости и вершины важно учитывать координаты и ориентацию плоскости, а также точность указанных данных и вычислений. В некоторых случаях может потребоваться применение дополнительных методов и инструментов для более точного определения взаимного расположения плоскости и вершины в пространстве.
Применение формул и теорем для проверки прохождения через вершину
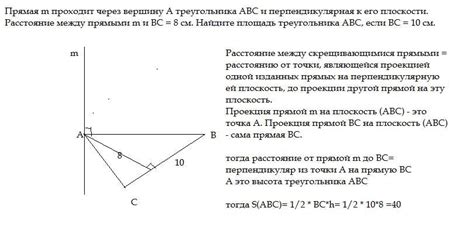
При решении геометрических задач особое внимание следует уделить проверке прохождения плоскости через вершину. Для этого существуют определенные формулы и теоремы, которые позволяют легко и достоверно проверить данное условие.
Одной из основных теорем, используемых для проверки прохождения через вершину, является теорема о перпендикулярных гранях. Если плоскость проходит через вершину, то грани, образующие эту вершину, перпендикулярны к данной плоскости.
Для проверки этого условия можно использовать следующую формулу:
- Уравнение плоскости: Ax + By + Cz + D = 0
- Координаты вершины: (x₀, y₀, z₀)
- Направляющие векторы граней: (a₁, b₁, c₁) и (a₂, b₂, c₂)
Если выполнено следующее условие:
- Ax₀ + By₀ + Cz₀ + D = 0
- a₁x₀ + b₁y₀ + c₁z₀ = 0
- a₂x₀ + b₂y₀ + c₂z₀ = 0
то плоскость проходит через вершину.
Таким образом, использование формул и теорем позволяет проверить прохождение плоскости через вершину и доказать данное условие с высокой степенью достоверности.
Использование специальных методов, таких как метод двойного пересечения
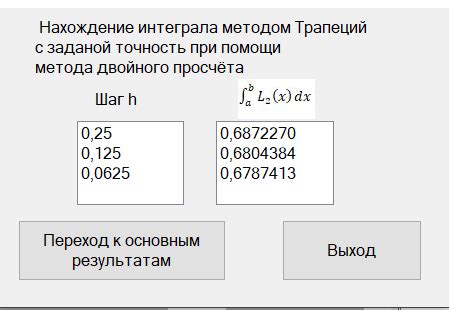
Принцип метода состоит в том, что для доказательства того, что плоскость проходит через заданную вершину, необходимо убедиться, что она пересекает две прямые, проходящие через эту вершину и являющиеся направляющими векторами плоскости.
Для начала выбираются две плоские прямые, которые проходят через заданную вершину. Затем применяется метод двойного пересечения:
- Находится пересечение первой прямой с плоскостью. Для этого составляется уравнение плоскости и подставляются координаты точек прямой в это уравнение. Если получается верное равенство, то первая прямая пересекает плоскость.
- Аналогично находится пересечение второй прямой с плоскостью.
- Если обе прямые пересекают плоскость, то это означает, что плоскость проходит через заданную вершину.
Использование метода двойного пересечения позволяет более уверенно и надежно доказать, что плоскость проходит через вершину. Этот метод также может применяться для доказательства, что плоскость проходит через другие элементы, такие как прямые или отрезки.
Рассмотрение различных случаев в зависимости от конкретных условий задачи

При решении задачи о доказательстве прохождения плоскости через вершину необходимо учитывать различные условия, которые могут быть заданы в задаче. В зависимости от этих условий, могут быть различные способы доказательства.
1. Если в задаче даны координаты вершины и уравнение плоскости, то можно подставить координаты вершины в уравнение плоскости и проверить, что получится верное равенство. Если равенство выполняется, значит, плоскость проходит через вершину.
2. Если в задаче даны координаты вершины и уравнение прямой, проходящей вдоль плоскости, то можно проверить, что вершина лежит на этой прямой. Если вершина лежит на прямой, то следовательно, плоскость проходит через вершину.
3. Если в задаче даны координаты трех точек, принадлежащих плоскости, то можно воспользоваться свойствами векторного произведения и проверить, что векторное произведение двух векторов, образованных от вершины до двух точек, равно нулю. Если векторное произведение равно нулю, то это значит, что плоскость проходит через вершину.
4. В некоторых случаях можно раскрыть уравнение плоскости и сравнить коэффициенты при переменных с координатами вершины. Если все коэффициенты равны, значит, плоскость проходит через вершину.
В каждом конкретном случае необходимо провести вычисления и анализировать полученные результаты, чтобы доказать или опровергнуть прохождение плоскости через вершину.
Анализ границ плоскости и вершины для доказательства их взаимного прохождения

Доказательство прохождения плоскости через вершину требует анализа границ плоскости и вершины, чтобы установить их взаимное пересечение или совпадение. В данной статье мы рассмотрим некоторые основные методы и принципы, которые могут быть использованы для подтверждения данного факта.
- Изучение координат: для начала, необходимо рассмотреть координаты вершины и уравнение плоскости. Если координаты вершины удовлетворяют уравнению плоскости, то это может свидетельствовать о прохождении плоскости через вершину.
- Анализ граничных точек: следующий шаг - рассмотреть граничные точки плоскости и убедиться, что вершина является одной из них. Если вершина leжит на границе плоскости, это указывает на то, что плоскость проходит через эту вершину.
- Расчет пересечений: в некоторых случаях может потребоваться провести дополнительные расчеты, чтобы установить пересечение плоскости с вершиной. Это может быть сделано, например, путем аппроксимации плоскости с использованием других тел и определения точек пересечения.
Важно отметить, что прохождение плоскости через вершину может быть доказано только с соответствующими анализом и расчетами. Данные методы позволяют установить и подтвердить данное положение.



