Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине. Доказать, что данный четырехугольник является параллелограммом, можно, зная его координаты в плоскости.
Чтобы показать, что четырехугольник является параллелограммом, необходимо проверить два условия. Во-первых, противоположные стороны должны быть параллельны. Во-вторых, противоположные стороны должны быть равны по длине. Если оба условия выполняются, то можно утверждать, что данный четырехугольник - параллелограмм.
Чтобы проверить параллельность двух сторон, можно воспользоваться формулой вычисления углового коэффициента прямой. Если угловые коэффициенты двух сторон равны, то эти стороны параллельны. Для проверки равенства длин противоположных сторон, можно вычислить расстояние между соответствующими точками на сторонах и сравнить их значения.
Критерии параллельности четырехугольника
- Стороны, соединяющие противоположные вершины, имеют одинаковую длину. Для этого можно использовать формулу расстояния между двумя точками в декартовой системе координат.
- Противоположные стороны параллельны. Для проверки этого условия можно использовать уравнения прямых, проходящих через соответствующие стороны, и проверить их равенство или параллельность.
- Диагонали равны по длине и пересекаются в точке, деля ее пополам. Для проверки можно использовать формулу расстояния между двумя точками и уравнение прямой, проходящей через две точки.
- Углы между сторонами, соединяющими одну и ту же вершину с противоположными сторонами, равны. Для этого можно использовать формулу расчета угла между двумя векторами.
Геометрические свойства параллелограмма
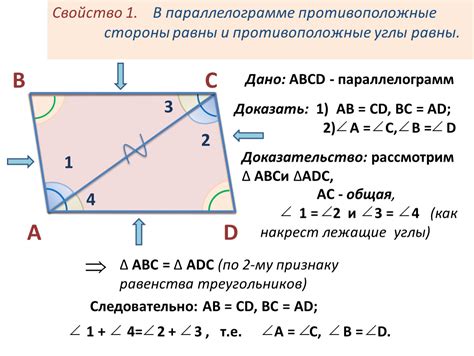
1. Противоположные стороны параллельны:
Это означает, что противоположные стороны параллелограмма лежат на параллельных прямых линиях. Таким образом, если мы проведем прямую линию через одну сторону параллелограмма, она будет параллельна другой стороне.
2. Противоположные стороны равны по длине:
Это означает, что длина противоположных сторон параллелограмма равна. Если мы измерим одну сторону параллелограмма, мы можем быть уверены, что противоположная сторона также будет иметь такую же длину.
3. Противоположные углы параллельны и равны:
Это означает, что параллельные стороны параллелограмма образуют равные углы с прямой, проведенной через другие параллельные стороны. Таким образом, если мы измерим угол между одной парой параллельных сторон, мы можем быть уверены, что угол между другой парой параллельных сторон также будет иметь такую же величину.
4. Диагонали параллелограмма делятся пополам:
Это означает, что диагонали параллелограмма делят его на две равные части. Таким образом, если мы проведем диагональ параллелограмма, она будет делить его на два равных треугольника.
Эти геометрические свойства помогают доказать, что четырехугольник является параллелограммом по его координатам.
Аналитические методы доказательства
Метод первых производных:
1. Вычисляем длины всех сторон четырехугольника, используя формулу расстояния между двумя точками в декартовой системе координат.
2. Проверяем, что противоположные стороны имеют одинаковые длины.
3. Вычисляем коэффициенты наклона прямых, проходящих через противоположные стороны, используя формулу наклона прямой в декартовой системе координат.
4. Проверяем, что коэффициенты наклона противоположных сторон равны.
5. Если все условия выполняются, то четырехугольник является параллелограммом.
Метод векторов:
1. Вычисляем координаты векторов, соединяющих противоположные вершины четырехугольника.
2. Проверяем, что векторы равны по модулю и направлению.
3. Если все условия выполняются, то четырехугольник является параллелограммом.
Примечание: В обоих методах следует быть внимательными при вычислениях и округлениях, чтобы избежать ошибок.
Вычисление уравнения прямой

Чтобы вычислить уравнение прямой, проходящей через две заданные точки, можно воспользоваться формулой определения уравнения прямой через координаты точек.
Пусть у нас есть две точки с координатами (x1, y1) и (x2, y2). Если прямая проходит через эти точки, то можно записать уравнение прямой в виде:
y - y1 = ((y2 - y1) / (x2 - x1)) * (x - x1)
Это уравнение прямой в общем виде. Здесь x и y - переменные, представляющие любую точку на прямой.
Подставляя координаты известных точек, получим конкретное уравнение прямой. Например, для точек (2, 1) и (4, 3) уравнение примет вид:
y - 1 = ((3 - 1) / (4 - 2)) * (x - 2)
Уравнение прямой позволяет определить ее положение и наклон. Например, если коэффициент перед x равен 0, то прямая параллельна оси y. Если коэффициент перед y равен 0, то прямая параллельна оси x. Если коэффициенты перед x и y не равны 0, то прямая имеет наклон.
Проверка соответствия четырехугольника критериям параллельности

Если оба критерия выполняются - противоположные стороны равны и противоположные углы равны, то можно сделать заключение, что четырехугольник является параллелограммом.
| Критерий параллельности | Условие проверки |
|---|---|
| Равенство противоположных сторон | Вычисляем длины противоположных сторон и сравниваем их |
| Равенство противоположных углов | Вычисляем значения противоположных углов и сравниваем их |



