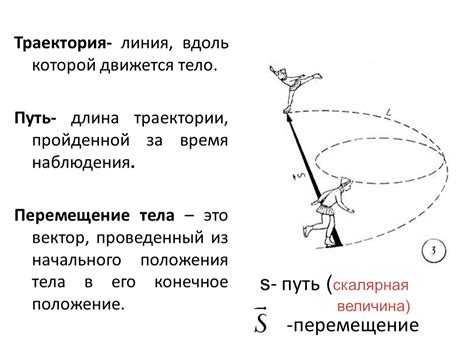
Координата прямолинейного движения является важной характеристикой объекта, двигающегося вдоль прямой линии. Определение координаты позволяет точно указать положение объекта на данной прямой и установить его относительное расположение по отношению к другим объектам или точкам.
Для определения координаты прямолинейного движения необходимо знать начальное положение объекта и его перемещение за определенный промежуток времени. Начальное положение обычно задается в виде числового значения, например, начальной точкой координатной оси. Перемещение определяется как разница между конечным и начальным положениями объекта.
Определение координаты прямолинейного движения также требует учета направления движения объекта. Если объект движется в положительном направлении оси, его координата будет положительной. Если объект движется в отрицательном направлении от начальной точки координатной оси, его координата будет отрицательной. Если объект остается на месте, то его координата будет равна начальному положению.
Определение координаты прямолинейного движения

Начальное положение объекта обычно задается в виде точки на оси координат. Задается координата x0. Если прямолинейное движение происходит только по горизонтальной оси, то это будет координата на оси x. Если движение происходит только по вертикальной оси, то это будет координата на оси y. Если движение происходит в пространстве, то задаются все три координаты – x, y и z.
Скорость объекта обозначается как v. Она может быть как постоянной, так и изменяться во времени. Если скорость постоянна, то координата объекта в момент времени t равна x(t) = x0 + v×t, где x(t) – координата объекта в момент времени t.
Если скорость изменяется, то необходимо знать уравнение движения. Обычно для задания уравнения движения используется закон движения, который может быть задан в виде функции или уравнения, описывающего зависимость координаты x от времени t. Например, x(t) = x0 + vt + at2/2, где a – ускорение объекта.
Для определения координаты прямолинейного движения необходимо знать начальное положение объекта и его скорость, а также уравнение движения, если скорость изменяется. Эти параметры позволяют определить координату объекта в любой момент времени и построить его траекторию на оси координат.
Координата в физике
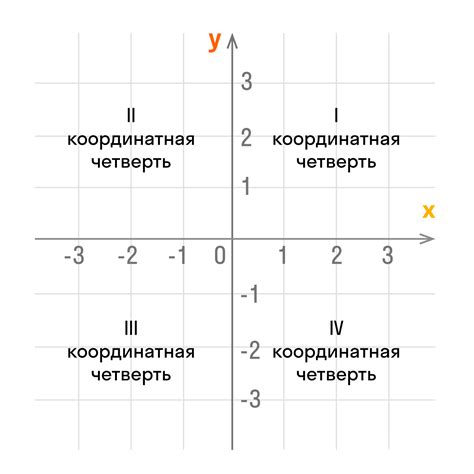
Координаты могут быть трехмерными (x, y, z) или двумерными (x, y). В двумерном случае, обычно используются координаты (x, y), где x - горизонтальная координата, а y - вертикальная координата.
Для определения координаты в прямолинейном движении необходимо знать начальное положение объекта и его перемещение относительно этого начального положения. Начальная координата (x0) задается в начальный момент времени, а перемещение (Δx) определяется разностью координат между конечным (x) и начальным положением (x0).
| Определение | Значение | Единицы измерения |
|---|---|---|
| Начальная координата (x0) | 153 | метры |
| Перемещение (Δx) | 65 | метров |
| Конечная координата (x) | x0 + Δx = 153 + 65 = 218 | метров |
Таким образом, координата в прямолинейном движении можно определить, зная начальную координату и перемещение объекта относительно нее. Эта информация позволяет точно определить положение объекта в пространстве.
Определение прямолинейного движения
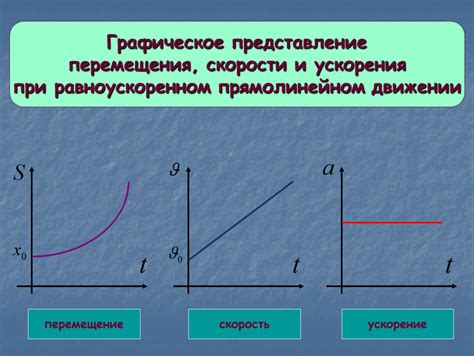
Для определения прямолинейного движения необходимо знать две основные характеристики:
- Траектория движения: для прямолинейного движения она должна быть прямой линией.
- Скорость движения: она должна быть постоянной величиной на протяжении всего движения. Это означает, что объект должен двигаться с одинаковой скоростью в любой момент времени.
Для определения координаты прямолинейного движения необходимо знать начальное положение объекта (координату) и его скорость. Зная эти данные, можно определить координату объекта в любой момент времени с помощью формулы:
x = x0 + v * t
где:
- x - координата объекта в конкретный момент времени;
- x0 - начальная координата объекта;
- v - скорость объекта;
- t - время, прошедшее с начала движения.
Таким образом, зная начальную координату и скорость движения, можно определить координату объекта в любой момент времени и трассировать его прямолинейное движение.
Системы определения координаты
Для определения координаты при прямолинейном движении могут использоваться различные системы и технологии. В зависимости от специфики задачи и требуемой точности измерения, выбирается подходящая система определения координаты.
Одной из самых распространенных систем является глобальная система навигации по спутникам (ГНСС), такая как GPS или ГЛОНАСС. Эти системы позволяют определить координату с высокой точностью на основе сигналов, принимаемых от спутников. Используя три и более спутника, можно определить трехмерные координаты.
Для определения координаты также можно использовать системы инерциальной навигации. Они основаны на принципе сохранения инерциальности движения объекта и позволяют определить его координаты на основе измерения ускорения и угловой скорости. Такие системы часто применяются в летательных и морских навигационных системах.
Еще одной системой определения координаты является система отслеживания по видео. Она использует видеокамеры, расположенные в разных точках, чтобы определить координату объекта на основе его отражения или изображения. Эта система может применяться в промышленных и транспортных системах.
В случае прямолинейного движения можно также использовать системы, основанные на измерении времени и расстояния. Например, система ультразвуковой локации может определить координату на основе времени задержки искаженного сигнала ультразвука от объекта.
В зависимости от задачи и условий применения, можно выбрать оптимальную систему определения координаты для прямолинейного движения. Важно учитывать требуемую точность, доступность и надежность системы, а также ее возможности в конкретной ситуации.
Методы измерения координаты

Существуют различные методы измерения координаты при прямолинейном движении. Они могут быть применены в зависимости от точности, доступных средств и условий эксперимента.
1. Использование линейки или ленты. Данный метод является наиболее простым и доступным, но его точность ограничена. Линейка или лента прочерчивается по направлению движения объекта, и координата определяется по отметке на шкале.
2. Стереолитография. Этот метод используется в современной научной практике и позволяет достичь высокой точности измерений. С помощью специальных устройств, основанных на принципе использования лазерных лучей, определяется координата объекта с высокой точностью.
3. Инерциальные системы навигации. Эти системы используются в авиации, космонавтике и некоторых других областях, где необходимо определить точное положение объекта в пространстве. Они работают на основе принципов инерциальных измерений и гравитации.
4. Глобальные спутниковые навигационные системы. Например, GPS. Они используются для определения координат объекта на поверхности Земли с высокой точностью. Работают на основе сигналов, передаваемых спутниками, и их приемом на специальном приемнике.
Выбор метода измерения координаты зависит от целей и требований эксперимента или задачи. Необходимо учитывать доступные средства и условия, а также обратить внимание на точность и требуемую точность измерений.
Аналитическое определение

Аналитическое определение координаты прямолинейного движения позволяет выразить изменение координаты точки на оси в зависимости от времени с использованием алгебраических выражений и математических операций.
Для определения координаты x точки в зависимости от времени t в случае прямолинейного движения можно использовать уравнение: x = x0 + v0t + (1/2)at2, где x0 - начальная координата точки, v0 - начальная скорость точки, a - ускорение точки.
Если значения начальной координаты x0, начальной скорости v0 и ускорения a известны, то можно использовать данное уравнение для определения значения координаты точки в любой момент времени.
Определение координаты в механике
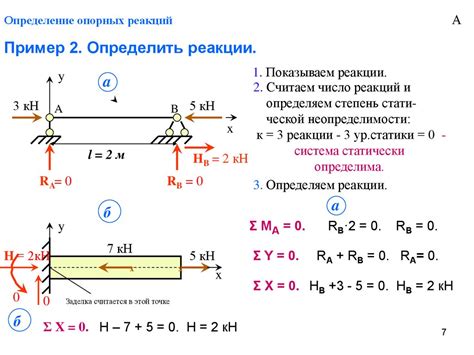
Для определения координаты в механике используются различные системы координат, такие как декартова система координат, полярная система координат и другие. Декартова система координат является наиболее широко применяемой системой координат в механике и состоит из двух осей - оси X и оси Y.
Координаты обычно измеряются в единицах длины, таких как метры или футы. Положительное направление оси X задается согласно выбранной системе координат, например, вправо, а положительное направление оси Y - вверх.
Определение координаты в механике может быть связано с движением объекта. В таком случае, координата изменяется в зависимости от времени. Существует несколько способов определения координаты в зависимости от вида движения, например, равномерное прямолинейное движение, равноускоренное прямолинейное движение и другие.
В рамках каждого вида движения используются соответствующие уравнения, которые позволяют определить значение координаты в зависимости от времени и других параметров движения. Например, для равномерного прямолинейного движения координата может быть определена по формуле x = x0 + vt, где x - значение координаты в заданный момент времени t, x0 - начальная координата, v - скорость.
| Тип движения | Формула для определения координаты |
|---|---|
| Равномерное прямолинейное движение | x = x0 + vt |
| Равноускоренное прямолинейное движение | x = x0 + v0t + (1/2)at^2 |
| Колебательное движение | x = A sin(ωt + φ) |
Важно учитывать, что для определения координаты в механике необходимо знать начальные условия движения, такие как начальную координату и начальную скорость. Кроме того, для различных типов движения применяются разные формулы, которые позволяют определить координату в зависимости от времени и других параметров движения.
Точность определения координаты

Определение координаты осуществляется с помощью различных методов и инструментов, таких как измерительные системы, глобальная навигационная спутниковая система (ГНСС) и лазерные дальномеры.
Однако, несмотря на использование современных технологий и высокоточных приборов, все методы имеют свою погрешность. Это может быть связано с физическими ограничениями приборов, атмосферными условиями или ошибками человека при проведении измерений.
Чтобы обеспечить максимальную точность определения координаты, рекомендуется использовать несколько методов и сравнивать полученные результаты. Также следует проводить повторные измерения для устранения случайных ошибок.
Важно также учитывать все факторы, которые могут оказывать влияние на точность измерений, такие как наличие помех, возможность возникновения систематических ошибок и др.
Для обеспечения высокой точности измерений необходимо также правильно обрабатывать полученные данные, использовать специализированное программное обеспечение и следовать рекомендациям производителей.
Практическое использование

Определение координаты прямолинейного движения имеет множество практических применений в различных областях. Ниже представлены некоторые из них:
| Область применения | Примеры |
|---|---|
| Физика |
|
| Машиностроение |
|
| Геодезия |
|
| Навигация |
|
| Компьютерная графика |
|
Это лишь некоторые примеры практического использования определения координаты прямолинейного движения. Данная методика находит применение во многих других областях, где требуется точное определение и контроль перемещения объектов или анализ и моделирование движения.
Примеры определения координаты

Существует несколько способов определения координаты прямолинейного движения:
1. Использование средств навигации
Современные технологии позволяют определить координату движения с помощью спутниковой навигационной системы, такой как GPS. При помощи специального приемника возможно получить точные координаты местоположения, которые могут быть использованы для определения прямолинейного движения.
2. Использование измерительных инструментов
В некоторых случаях можно использовать измерительные инструменты, такие как лазерные дальномеры или инкрементальные энкодеры, для определения координаты прямолинейного движения. Эти инструменты позволяют измерять расстояние или перемещение объекта и получить точные значения его координаты.
3. Использование математических расчетов
В некоторых случаях можно использовать математические расчеты для определения координаты прямолинейного движения. Например, если известна начальная координата объекта, его скорость и время движения, то можно определить его текущую координату с помощью формулы x = x0 + vt, где x - текущая координата, x0 - начальная координата, v - скорость, t - время движения.
Использование этих методов позволяет определить координату прямолинейного движения с высокой точностью и достоверностью.



