А и Б являются основными понятиями в теории прямоугольников. Прямоугольник - это плоская геометрическая фигура, у которой противоположные стороны параллельны и все углы прямые. Он является одной из наиболее распространенных и изучаемых фигур в геометрии.
В прямоугольнике есть две оси - горизонтальная и вертикальная. Ось горизонтальная называется осью А, а ось вертикальная - осью Б. Они пересекаются в точке O, которая является началом координат прямоугольной системы координат.
Оси А и Б в прямоугольнике имеют свои основные свойства. Ось А представляет собой горизонтальную линию, которая образует основу прямоугольника. Ось Б - вертикальная линия, которая стоит под прямым углом к оси А и проходит через середину основы.
Определение прямоугольника
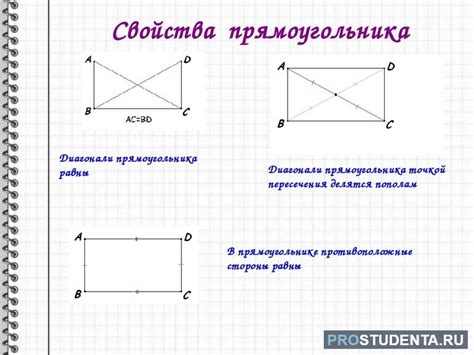
В прямоугольнике противоположные стороны равны между собой. Также противоположные стороны параллельны друг другу. Диагонали прямоугольника имеют одинаковую длину и делят его на два равных прямоугольных треугольника.
Следует отметить, что прямоугольник может считаться частным случаем квадрата, у которого все стороны равны. И наоборот, любой квадрат можно рассматривать как прямоугольник.
Прямоугольники широко используются в геометрии и на практике. Они могут быть использованы для моделирования строений, размещения объектов на плоскости или вычисления площадей.
Понятие прямоугольника в геометрии
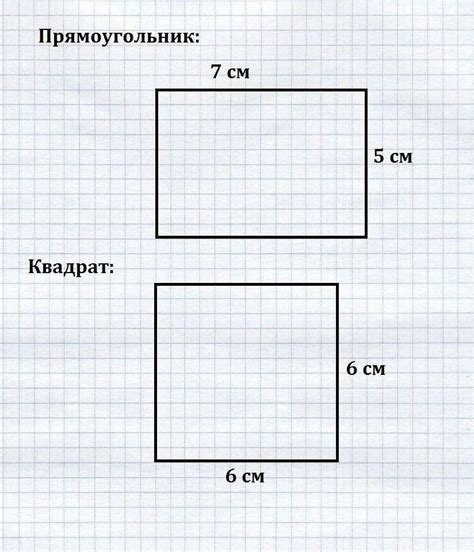
Основные свойства прямоугольника:
- Противолежащие стороны прямоугольника параллельны друг другу;
- Углы прямоугольника все равны 90 градусов;
- Диагонали прямоугольника равны между собой и делят его на два равных прямоугольных треугольника;
- Периметр прямоугольника вычисляется по формуле: P = 2(a + b), где a и b - длины сторон прямоугольника;
- Площадь прямоугольника вычисляется по формуле: S = a*b, где a и b - длины сторон прямоугольника.
Прямоугольники широко используются в разных областях. Например, в архитектуре они используются при планировке помещений и строительстве зданий. В математике и геометрии они являются основой для изучения других многогранников и фигур.
Свойства прямоугольника
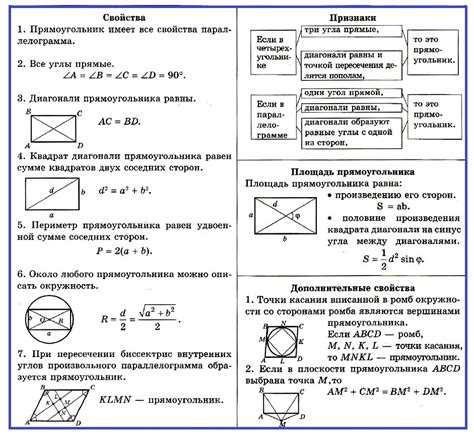
Свойства прямоугольника включают:
| Стороны: | параллельные стороны равны по длине |
| Углы: | все углы являются прямыми (равны 90 градусам) |
| Диагонали: | диагонали равны по длине и пересекаются в центре прямоугольника |
| Периметр: | сумма длин всех четырех сторон |
| Площадь: | произведение длин основных сторон |
Свойства прямоугольника важны для его изучения и решения геометрических задач. Они помогают определить и использовать его характеристики при решении различных задач и расчете его параметров.
Углы прямоугольника
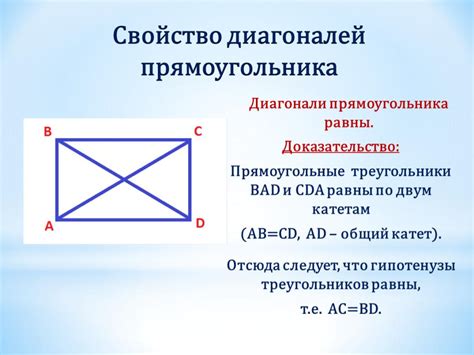
В прямоугольнике существуют два вида углов:
Прямые углы - это углы, которые равны 90 градусам и обозначаются символом ∠. В прямоугольнике имеется четыре прямых угла. Каждый угол прямоугольника может быть обозначен буквами A,B,C и D.
Равные углы - это углы, которые имеют одинаковую меру и обозначаются одинаковыми буквами. В прямоугольнике имеются две пары равных углов - А и С, B и D.
Основные формулы прямоугольника
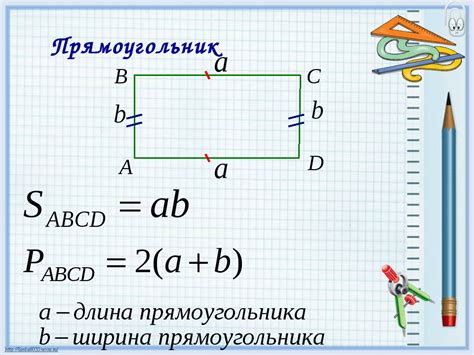
Площадь прямоугольника можно вычислить по формуле:
| Площадь | = | Длина | × | Ширина |
| S | = | a | × | b |
Периметр прямоугольника можно найти по формуле:
| Периметр | = | 2 × (Длина | + | Ширина) |
| P | = | 2 × (a | + | b) |
Диагональ прямоугольника можно найти с помощью теоремы Пифагора:
| Диагональ | = | √ (Длина | ^2 | + | Ширина | ^2) |
| d | = | √ (a | ^2 | + | b | ^2) |
Зная хотя бы два измерения - длину, ширину, площадь или периметр - можно рассчитать остальные характеристики прямоугольника. Эти формулы помогут упростить расчеты и получить необходимые значения.
Периметр прямоугольника
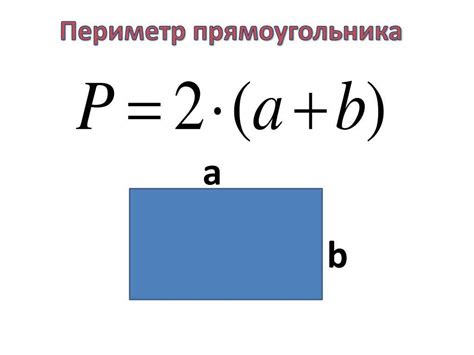
Периметр = 2(А + Б)
Для примера, если сторона А прямоугольника равна 5 см, а сторона Б равна 8 см, то периметр будет:
Периметр = 2(5+8) = 2 * 13 = 26 см
Таким образом, периметр прямоугольника – это длина пути, который нужно пройти вдоль его границы.



