Функция квадратичного типа, график которой представлен уравнением f(x) = x^2, является одной из наиболее известных и часто используемых функций в математике. Возведение числа в квадрат всегда дает положительное значение, поэтому график функции f(x) = x^2 представляет из себя параболу, направленную вверх.
Эта функция широко применяется во многих областях науки и инженерии. Она может использоваться для моделирования различных явлений и процессов, а также для решения задач оптимизации. График функции f(x) = x^2 имеет некоторые особенности, которые помогают понять поведение функции в различных точках.
Например, точка с координатами (0,0) является вершиной параболы. Значение функции f(x) = x^2 при x = 0 равно 0. При положительных и отрицательных значениях аргумента функции, квадрат аргумента будет положительным числом. Это означает, что функция f(x) = x^2 не пересекает ось OX и всегда остается выше нее.
Определение графика функции f(x) = x^2
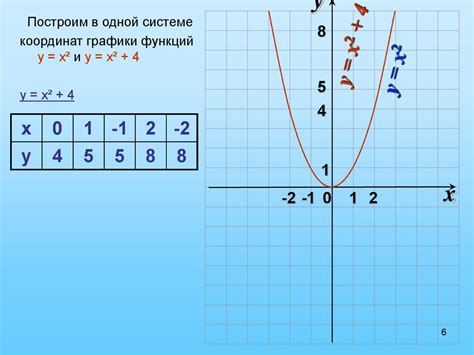
График функции f(x) = x^2 представляет собой множество точек, координаты которых соответствуют значениям функции при различных значениях аргумента x. Для построения графика функции f(x) = x^2, необходимо выбрать несколько значений для переменной x, вычислить значения функции при этих значениях и отметить полученные точки на координатной плоскости.
Функция f(x) = x^2 описывает квадратичную зависимость между переменными x и y. График этой функции имеет форму параболы, которая открывается вверх, если коэффициент при x^2 положителен.
На графике функции f(x) = x^2 можно отметить такие особенности:
- Точка пересечения с осью ординат (0, 0) - начало координат;
- Симметричность относительно оси ординат;
- Минимальное значение функции равно 0 и достигается при x = 0;
- Функция возрастает при значении x отрицательное бесконечность до 0 и возрастает при значении x от 0 до положительного бесконечности;
График функции f(x) = x^2 может быть полезен для изучения свойств квадратичной функции и анализа ее поведения при изменении аргумента.
Определяем основные характеристики функции

Вершина параболы: Для функции f(x) = x^2 вершина находится в точке (0, 0). Это означает, что является точкой минимума (если коэффициент при x^2 был отрицательным, вершина была бы максимумом).
Направление открытия: Парабола этой функции открывается вверх, так как коэффициент при x^2 положительный (равен 1).
Ось симметрии: Ось симметрии параболы функции f(x) = x^2 проходит через вершину и параллельна оси y. То есть она проходит через точку (0, 0).
Начало координат: Точка начала координат (0, 0) также является точкой пересечения параболы с осью x и осью y. Это означает, что функция f(x) = x^2 проходит через эту точку.
Увеличение и убывание: Функция f(x) = x^2 возрастает на всей числовой прямой, кроме точки x = 0, где достигается ее минимум.
Изучение основных характеристик функции f(x) = x^2 помогает понять и визуализировать ее поведение и использовать ее в различных математических и научных задачах.
Как построить график функции f(x) = x^2
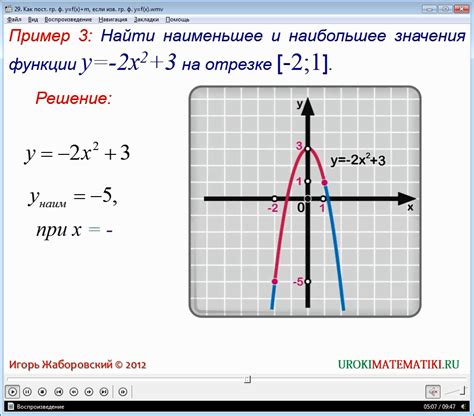
- Начните с создания координатной плоскости, где оси X и Y пересекаются в точке (0,0). Ось X будет горизонтальной, а ось Y - вертикальной.
- Постройте несколько точек со значениями x и y, чтобы получить представление о форме графика. Вы можете выбрать любые значения x и посчитать соответствующие значения y, подставляя их в функцию f(x) = x^2.
- После того, как вы построили несколько точек, соедините их линиями, чтобы получить гладкий график. Чем больше точек вы используете, тем более точный будет график.
График функции f(x) = x^2 является параболой, открывшейся вверх. Он имеет вершину в точке (0,0) и симметричен относительно оси Y.
Построение графика функции f(x) = x^2 может помочь визуализировать ее поведение и понять, как она изменяется при изменении значения x. Это также может быть полезным при решении математических задач и анализе функций.
Особенности и интерпретация графика функции
- Симметрия: график функции симметричен относительно оси OY. Это означает, что если для какого-то значения x функция возвращает значение y, то для -x она будет возвращать тоже значение y.
- Вершина параболы: вершина графика функции находится в точке (0, 0). Это значит, что при x = 0 значение функции равно 0.
- Ветви параболы: график функции имеет две ветви, которые направлены вверх. Это означает, что при увеличении значения x, значение функции также увеличивается.
- Выпуклость: график функции является выпуклым вверх. Это означает, что на каждом отрезке графика, наклонная прямая будет лежать выше самой кривой.
- Нули функции: нулями функции являются точки (0, 0) и (-x, 0), где x - любое ненулевое число. Это можно интерпретировать как то, что функция равна 0 при x = 0 и x = -|x|.
- Увеличение значения функции: при увеличении значения x, значение функции увеличивается квадратично. Это означает, что при изменении аргумента, значение функции возрастает быстрее, чем линейно.



