Ломаная линия - это графический элемент, состоящий из соединенных прямых линий, образующих замкнутую или незамкнутую фигуру. В геометрии, ломаные линии часто используются для представления графиков функций, статистических данных или контуров объектов.
Для создания ломаной линии 1 класс необходимо знать координаты точек, через которые она проходит. Координаты точек представляют собой пары чисел (x, y), где x - это горизонтальное положение точки, а y - вертикальное положение точки.
Чтобы построить ломаную линию, соедините точки прямыми отрезками в порядке их следования. Ломаная линия может быть замкнутой или незамкнутой. В случае замкнутой ломаной линии последняя точка соединяется с первой точкой.
Ломаная линия 1 класс может быть использована в различных областях, таких как архитектура, дизайн, инженерия и даже компьютерная графика. Она позволяет наглядно отобразить данные и создать яркий визуальный эффект. Важно учитывать, что для построения ломаной линии 1 класс необходимо иметь базовые знания геометрии и умение работать с координатной плоскостью.
Длина, направление, точки

Длина ломаной линии 1 класс вычисляется путем сложения длин всех отрезков, из которых она состоит. Для этого необходимо знать координаты всех точек, через которые проходит ломаная линия. Длина каждого отрезка определяется по формуле длины отрезка, которая вычисляется как разность координат его конечных точек по соответствующим осям.
Направление ломаной линии 1 класс определяется углом, под которым она пролегает относительно оси абсцисс. Этот угол вычисляется как арктангенс отношения разности координат по оси ординат к разности координат по оси абсцисс последних двух точек ломаной линии.
Точки ломаной линии являются основными элементами, через которые проходит ломаная линия. Они задаются координатами на плоскости и определяют форму ломаной. Чем больше точек, тем более сложной может быть форма ломаной линии. Количество точек зависит от предназначения и конкретной задачи, которую необходимо решить с помощью данной ломаной линии.
Периметр, площадь, градиент
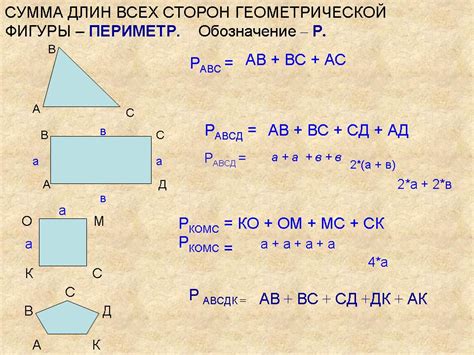
П = d1 + d2 + ... + dn
Площадь ломаной линии - это площадь выпуклого многоугольника, образованного ломаной линией и отрезками, проведенными от вершин ломаной линии до начальной точки координат. Для нахождения площади используется формула Гаусса:
S = (x1y2 + x2y3 + ... + xn-1yn + xn y1 - x2y1 - x3y2 - ... - yn x1) / 2
где (xi, yi) - координаты вершин ломаной линии.
Градиент ломаной линии - это угловой коэффициент прямой, проходящей через начальную и конечную точку ломаной линии. Градиент можно найти, используя разницу координат y и x:
К = (y2 - y1) / (x2 - x1)
где (x1, y1) и (x2, y2) - координаты начальной и конечной точки ломаной линии.
Углы, расстояние, коэффициент
Ломаная линия 1 класс состоит из отрезков, углов и расстояний между точками.
Углы в ломаной линии 1 класс могут быть прямыми (равны 90 градусам), острыми (меньше 90 градусов) или тупыми (больше 90 градусов).
Расстояние между двумя точками в ломаной линии 1 класс определяется как длина отрезка, соединяющего эти точки. Расстояние может быть измерено в единицах длины, таких как метры или сантиметры.
Коэффициент – это отношение длины ломаной линии 1 класс к длине отрезка, который соединяет первую и последнюю точки. Коэффициент может быть положительным или отрицательным, в зависимости от того, в каком направлении ломаная линия изгибается от начальной точки к конечной.
Прямая, кривая, сегмент

Прямая является основным элементом ломаной линии 1 класс. Она представляет собой самый простой сегмент, который является также кратчайшим путем между двумя точками. Прямая не имеет изгибов и состоит из одного сегмента.
Кривая – это сегмент ломаной линии, который имеет изгибы. Она состоит из нескольких последовательных сегментов, подобных дугам различных радиусов. Каждый из сегментов кривой соединяет две точки и формирует плавный переход между ними, создавая изгиб кривой.
Сегмент – это участок линии, ограниченный двумя точками. Каждый сегмент может быть прямым или кривым, в зависимости от формы ломаной линии. Сегменты ломаной линии могут иметь различную длину и углы между соседними сегментами, что придает ломаной линии разнообразные формы и конфигурации.
Отрезок, вершина, закономерность
Ломаная линия 1 класс состоит из отрезков, которые соединяются в вершины. Отрезок представляет собой участок линии между двумя точками, который можно изобразить прямой.
Вершина является точкой пересечения двух отрезков. Она может быть как внутренней, так и внешней, в зависимости от того, как отрезки сходятся в данной точке.
Ломаная линия 1 класс может иметь различные закономерности. Например, отрезки могут быть одинаковой длины и идти последовательно друг за другом, или же они могут иметь разную длину и принимать разные направления.
Соединение, прямолинейность, аппроксимация
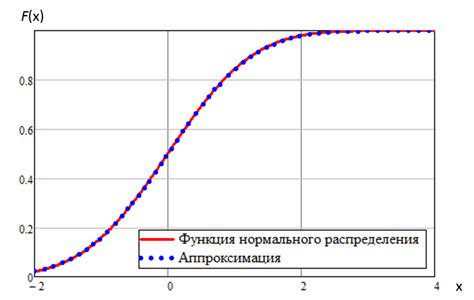
Ломаная линия 1 класс составляет основу для графического представления различных объектов и данных. Она представляет собой серию отрезков, соединяющих последовательные точки на плоскости. Соединение точек обеспечивает непрерывность ломаной линии и позволяет отображать изменение значений величин.
Прямолинейность ломаной означает, что каждый отрезок линии является прямым. Это позволяет использовать ломаную для решения различных задач, таких как построение графиков функций или отображение результатов измерений.
Ломаная линия 1 класс может быть использована для приближенного представления плавных кривых, используя метод аппроксимации. Для этого каждый отрезок ломаной заменяется кривой с заданной функциональной зависимостью, для наилучшего соответствия исходной форме.
Регрессия, функция, точность

Функция, описывающая ломаную линию, может быть представлена в виде алгоритма, который определяет значения y для заданных значений x. Для этого необходимо вычислить значение y для каждого отрезка и точки на нем, используя уравнение прямой.
Точность приближения ломаной линии может быть определена сравнением вычисленных значений y с исходными значениями, которые заданы в исходных данных. Чем ближе значения, тем точнее приближение. Оценка точности может быть выполнена, например, с помощью коэффициента детерминации R², который показывает, какая часть дисперсии зависимой переменной объяснена моделью. Чем ближе значение R² к 1, тем лучше модель объясняет данные.
| Номер точки | x | y |
|---|---|---|
| 1 | 2 | 5 |
| 2 | 4 | 9 |
| 3 | 6 | 13 |
| 4 | 8 | 17 |
Точка перегиба, радиус, уравнение
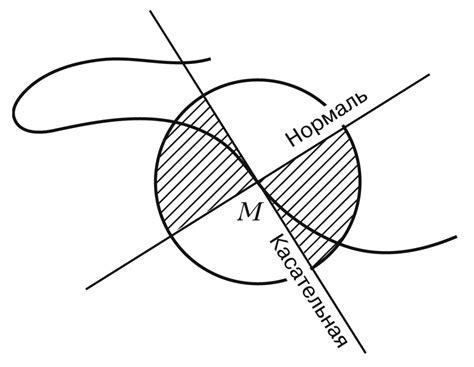
Точка перегиба - это точка на ломаной, в которой направление касательной к кривой меняется. Она обозначает место, где кривая меняет свое направление. Точка перегиба может быть найдена путем решения уравнения второй производной кривой и приравнивания его к нулю.
Радиус кривизны - это величина, которая указывает, насколько кривая отклоняется от прямой линии в данной точке. Радиус кривизны можно найти, используя формулу:
r = (1 + (dy/dx)^2)^(3/2) / |d^2y/dx^2|
где dy/dx - производная функции по x, d^2y/dx^2 - вторая производная функции по x.
Уравнение ломаной линии 1 класса может быть записано как уравнение прямой. Для этого необходимо определить начальную точку ломаной и найти угловой коэффициент наклона прямой. Угловой коэффициент можно найти путем деления изменения y на изменение x между двумя соседними точками на ломаной.
Итак, ломаная линия 1 класса может иметь точку перегиба, радиус кривизны и уравнение прямой, которая ее аппроксимирует.
Координаты, тангенс, окружность
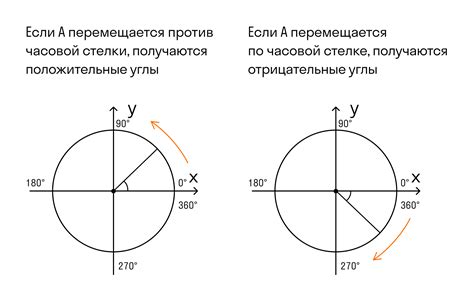
Тангенс угла наклона ломаной линии 1 класс определяется как отношение разности вертикальных координат (y2 - y1) к горизонтальной разности координат (x2 - x1), где (x1, y1) и (x2, y2) - координаты двух точек на ломаной линии.
Ломаная линия 1 класс может быть также аппроксимирована окружностью. Для этого точки на ломаной линии выбираются таким образом, чтобы соседние отрезки образовывали равные углы между собой. Такая окружность называется описанной окружностью и имеет центр, радиус и углы.
Экстремум, наклон, отношение

Экстремум
Ломаная линия 1 класс может иметь экстремумы, то есть точки, в которых она достигает максимального или минимального значения. Экстремумы могут быть локальными, когда они находятся внутри участка ломаной, или глобальными, когда они находятся на его концах.
Наклон
Наклон ломаной линии 1 класс определяется по разности значений её координат. Если разность положительная, то ломаная идет вверх, если отрицательная – вниз. Если разность равна нулю, то выполняется вертикальная линия.
Отношение
Коэффициенты наклона ломаной линии 1 класс могут быть разными. Они могут быть положительными, отрицательными или равными нулю. Отношение между этими коэффициентами позволяет определить угол наклона.



