График функции у(x) представляет собой визуальное отображение зависимости между аргументом x и значением функции у в плоскости.
График представляет из себя совокупность точек, каждая из которых имеет координаты (x, у). При построении графика учитываются все значения аргумента x и соответствующие им значения функции у. Эти точки соединяются специальными линиями, которые образуют гладкую кривую, показывающую изменение функции у относительно аргумента x.
График функции у(x) может принимать различные формы, в зависимости от типа функции и ее свойств. Например, график линейной функции представляет собой прямую линию, а график квадратичной функции имеет форму параболы. Важно заметить, что график может быть разным для разных областей определения функции и варьироваться в зависимости от значений параметров функции.
Определение графика функции
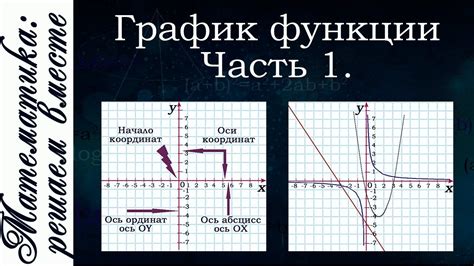
Для построения графика функции необходимо знать значения функции для различных значений независимой переменной. Обычно используется декартова система координат, где ось абсцисс (горизонтальная ось) отображает значения независимой переменной, а ось ординат (вертикальная ось) - значения функции.
График функции может иметь различные формы, такие как прямые линии, параболы, гиперболы и другие сложные кривые. Форма графика зависит от функции и ее математического выражения.
На графике функции можно определить различные характеристики, такие как экстремумы (максимумы и минимумы), точки пересечения с осями координат, асимптоты и другие важные точки.
График функции является важным инструментом в математике и науке, так как он помогает визуализировать и анализировать зависимость между различными переменными и предсказывать их поведение в рамках заданной функции.
| Пример графика функции | Описание |
|---|---|
 | Пример графика функции y = f(x), где y - значение функции, а x - независимая переменная. |
Факторы, влияющие на график функции
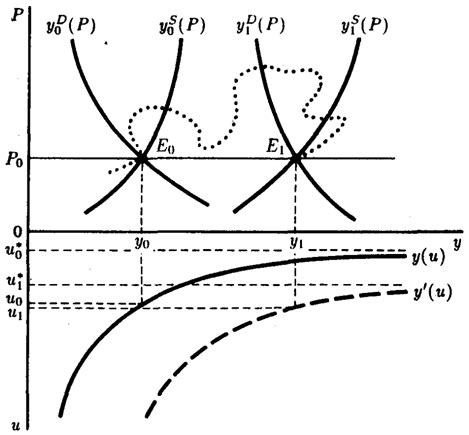
- Функциональная форма: Зависимость y от x может быть задана разными функциональными формами, такими, как линейная, квадратичная, экспоненциальная, логарифмическая и т.д. Каждая из этих форм описывает различное поведение функции и ведет к формированию соответствующего графика.
- Коэффициенты функции: Значения коэффициентов функции у(x) также оказывают влияние на внешний вид графика. Изменение коэффициентов может привести к смещению, повороту или масштабированию графика.
- Диапазон значений: Изменение диапазона значений аргумента x и значения функции y может изменить масштаб и пропорции графика.
- Асимптоты: Некоторые функции могут иметь вертикальные или горизонтальные асимптоты, которые ограничивают поведение графика на бесконечности.
- Нули функции: Нули функции, то есть значения аргумента, при которых функция равна нулю, могут влиять на форму графика, определяя точки пересечения с осью x.
- Симметрия: Функция может быть симметричной относительно оси x, оси у или начала координат, что отразится на симметрии ее графика.
Изучение этих факторов помогает более глубоко понять свойства и особенности графика функции у(x), а также использовать их для анализа и решения математических задач.
Примеры графиков функций
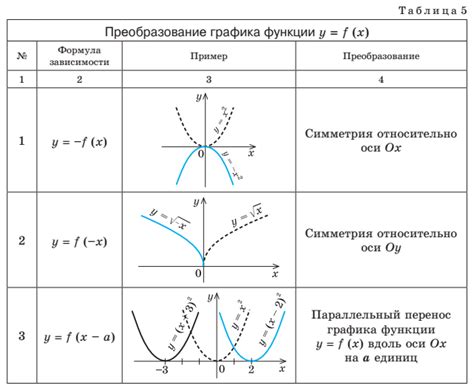
Давайте рассмотрим несколько примеров графиков функций, чтобы лучше понять, как они выглядят и какие особенности обладают.
1. График линейной функции:
- Уравнение функции: y = mx + b
- График является прямой линией с угловым коэффициентом m и точкой пересечения с осью y равной b.
- Если m > 0, линия будет возрастать отлево направо. Если m
2. График квадратичной функции:
- Уравнение функции: y = ax^2 + bx + c
- График является параболой, либо ветвями вверх, если a > 0, либо ветвями вниз, если a
- Вершина параболы имеет координаты (-b/(2a), f(-b/(2a))), где f(-b/(2a)) является значением функции в этой точке.
3. График показательной функции:
- Уравнение функции: y = a^x, где a > 0 и a ≠ 1
- График возрастает или убывает экспоненциально в зависимости от значения a.
4. График синусоидальной функции:
- Уравнение функции: y = A sin(B(x - C)) + D
- График является синусоидой со значением амплитуды A, периода 2π/B, горизонтальным сдвигом C и вертикальным сдвигом D.
Это всего лишь несколько примеров графиков функций, и в реальности их может быть гораздо больше. Каждая функция имеет свои особенности и специфический график, и изучение их помогает нам лучше понять их свойства и поведение.



