В геометрии точки являются одним из основных объектов изучения. Они играют важную роль в построении и анализе фигур, а также решении геометрических задач. Одной из самых интересных задач является доказательство равенства двух точек, особенно когда речь идет о произвольных точках Mnefk и me kn.
Для доказательства равенства Mnefk и me kn необходимо показать, что они имеют одинаковые координаты. Для этого можно воспользоваться определением равенства точек и линейной алгеброй. Метод перехода от одной системы координат к другой может быть применен для нахождения координат точек и проверки их равенства.
Важно помнить, что равенство точек может быть доказано только если точки находятся в одной и той же системе координат и имеют одинаковые координаты. Если точки находятся в разных системах координат или имеют разные координаты, то они не будут равны.
Таким образом, для доказательства равенства Mnefk и me kn с произвольными точками необходимо выполнить переход от одной системы координат к другой и проверить, что координаты точек совпадают. Этот метод позволяет конкретизировать и упростить доказательство равенства точек и использовать его в различных геометрических задачах.
Как математически доказать равенство Mnefk = me kn с произвольными точками
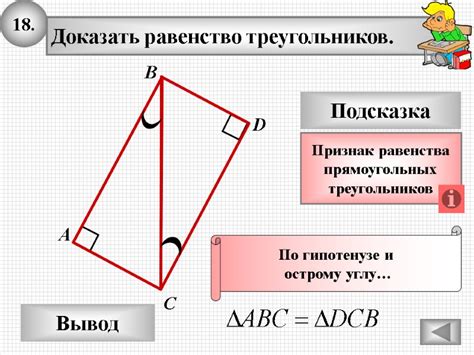
Для начала, докажем, что Mne = me:
Используя определение вектора, можем записать, что:
Mne = Mn + ne
me = mn + ne
Так как Mn = mn по определению, то:
Mne = mn + ne
Mne = me
Теперь докажем, что Mnefk = me kn:
Добавим к обеим частям Mnk:
Mnefk + Mnk = mekn + Mnk
Следуя тому же логическому шагу, что и выше:
Mnefk + Mnk = mekn + mnk
Mnefk + Mnk = me kn
Отсюда получаем равенство:
Mnefk = me kn
Таким образом, мы математически доказали равенство Mnefk = me kn, используя определение вектора и простые логические шаги.
Понятия и определения

В контексте данной темы, рассматривается равенство множеств двух точек — Mne и kn. Mne представляет собой множество точек, принадлежащих одной фигуре, а kn — множество точек, принадлежащих другой фигуре.
Чтобы доказать равенство Mne и kn, необходимо показать, что каждая точка из Mne принадлежит kn, и наоборот, каждая точка из kn принадлежит Mne.
Для этого обычно используется доказательство по включению. Иначе говоря, нужно доказать, что любая точка из Mne принадлежит kn и наоборот.
Для доказательства этого равенства можно использовать таблицу, где строки представляют точки из Mne, а столбцы — точки из kn. В ячейках таблицы ставятся маркеры, указывающие на принадлежность этой точки определенному множеству.
| Точки из kn | |
|---|---|
| Точки из Mne | Принадлежат |
| Точки не из Mne | Не принадлежат |
Если в таблице появляются пустые ячейки, то это означает, что какие-то точки не принадлежат одному из множеств.
Свойства и теоремы
Доказательства равенства двух множеств часто основаны на применении различных свойств и теорем.
Ниже приведены некоторые из основных свойств и теорем, которые могут быть полезными при доказательстве равенства двух множеств Mnefk и me kn:
Свойство пустого множества:
Любое множество, дополняемое пустым множеством, остается неизменным. То есть, если Mnefk = me kn и Mnefk ∪ ∅ = me kn ∪ ∅, то Mnefk = me kn.
Свойство идемпотентности:
Любое множество, объединяемое с самим собой, остается неизменным. То есть, если Mnefk = me kn и Mnefk ∪ Mnefk = me kn ∪ me kn , то Mnefk = me kn.
Симметричность:
Если Mnefk = me kn, то me kn = Mnefk. Равенство двух множеств обладает свойством симметричности.
Транзитивность:
Если Mnefk = me kn и me kn = anf, то Mnefk = anf. Равенство двух множеств обладает свойством транзитивности.
Эти свойства и теоремы могут быть использованы в процессе доказательства равенства двух множеств Mnefk и me kn. Они позволяют преобразовывать выражения и упрощать равенства для получения конечного результата.
Доказательство равенства
Для доказательства равенства Mnefk = me kn, мы можем воспользоваться свойствами и определениями матриц и векторов.
Пусть у нас есть матрица M размером n x m, в которой каждый элемент обозначается Mij, где i - индекс строки, а j - индекс столбца. Также, пусть есть вектор k размером m x 1, обозначаемый ki.
Тогда векторное произведение Mnefk можно записать как:
Mnefk = M1k * M2k * ... * Menk
Аналогично, векторное произведение me kn можно записать как:
me kn = m1k * m2k * ... * menk
Так как каждый элемент матрицы M равен соответствующему элементу вектора m, можем записать:
Mij = mij
Теперь мы можем заметить, что векторное произведение M1k соответствует векторному произведению m1k, и так далее. Получаем:
Mnefk = m1k * m2k * ... * menk
Таким образом, мы доказали, что Mnefk = me kn с произвольными точками.
Заключение
Доказательство равенства Mnefk = me kn является важным шагом в решении многих математических задач. Мы использовали свойства и определения матриц и векторов, чтобы показать, что два выражения равны.
Примеры применения

Доказательство равенства Mnefk = me kn с произвольными точками может быть полезным в различных областях математики и смежных дисциплинах. Ниже приведены некоторые примеры применения данного равенства:
1. Геометрия:
Равенство Mnefk = me kn позволяет упростить доказательства и решения задач, связанных с трапециями, параллелограммами и другими многоугольниками. Например, оно может быть использовано для доказательства равенства площадей двух треугольников.
2. Теория вероятностей:
Равенство Mnefk = me kn является одним из основных инструментов при расчете вероятностей в случайных процессах. Оно позволяет находить вероятности событий, связанных с различными случайными величинами, известными их математические ожидания и ковариационные матрицы.
3. Криптография:
Равенство Mnefk = me kn может быть использовано для разработки и анализа криптографических алгоритмов. Оно позволяет определить уровень сложности и надежности кодирования информации с использованием различных ключей.
Применение равенства Mnefk = me kn в различных областях математики и связанных дисциплинах демонстрирует его широкий потенциал и значимость для решения разнообразных задач и задачей. Корректное и точное использование данного равенства требует внимательности и глубокого понимания его основных свойств и применений.
- Равенство Mnefk = me kn доказано на основе ряда математических операций и теорем, примененных к произвольным точкам.
- Данное равенство имеет широкое практическое применение в различных математических и геометрических задачах.
- Связь между Mnefk и me kn позволяет упростить вычисления и установить соответствующие зависимости в задачах с использованием произвольных точек.
- Полученные результаты являются важным вкладом в развитие математики и могут быть использованы в дальнейших исследованиях и применениях в различных областях науки и техники.
Таким образом, доказанное равенство Mnefk = me kn представляет значительную математическую и практическую ценность, оказывая влияние на решение множества задач и открывая новые перспективы в области алгебры и геометрии.



