Градиентный спуск является одним из ключевых алгоритмов в машинном обучении, особенно в области нейронных сетей. Этот метод используется для обучения нейронных сетей путем минимизации функции потерь. Градиентный спуск позволяет передвигаться по пространству параметров модели в направлении наискорейшего убывания функции потерь, чтобы найти оптимальные значения параметров и достичь наилучших результатов.
Градиентный спуск основывается на вычислении градиента функции потерь по параметрам модели. Градиент представляет собой вектор, указывающий направление наиболее быстрого возрастания функции. Путем изменения параметров модели в противоположном направлении градиента, мы можем постепенно приближаться к минимуму функции, что соответствует нахождению оптимальных значений параметров модели.
Процесс градиентного спуска может быть представлен как итерационный алгоритм, который состоит из нескольких шагов. На каждой итерации мы вычисляем градиент функции потерь по параметрам модели, затем обновляем параметры, используя полученный градиент. Этот процесс повторяется до тех пор, пока не будет достигнуто условие остановки, такое как достижение определенного количества итераций или сходимость значений параметров.
Градиентный спуск может иметь различные варианты, такие как стохастический градиентный спуск или мини-батч градиентный спуск. Они отличаются способом вычисления градиента и обновления параметров. Однако, основной принцип остается неизменным: использование градиента для определения направления движения и обновление параметров модели с целью минимизации функции потерь.
Определение градиентного спуска
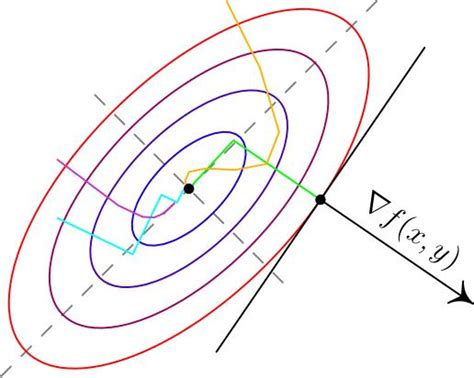
Градиентный спуск получает свое название из математической концепции градиента, который является вектором, указывающим направление наиболее быстрого возрастания функции в данной точке. Цель градиентного спуска - найти экстремум (минимум или максимум) функции путем последовательного обновления весовых коэффициентов сети.
Алгоритм градиентного спуска работает следующим образом: для каждого весового коэффициента модели он вычисляет частные производные функции потерь по этому коэффициенту. Затем он определяет направление изменения этого коэффициента, учитывая значение градиента. По мере продвижения по градиентному направлению алгоритм обновляет весовые коэффициенты с заданным шагом (скоростью обучения), осуществляя градиентный спуск.
Градиентный спуск используется в процессе обучения нейронных сетей для настройки ее параметров таким образом, чтобы минимизировать ошибку сети. Он является основой для многих других алгоритмов оптимизации и позволяет достигать высокой точности в обучении нейронных сетей.
Принцип работы градиентного спуска

Алгоритм градиентного спуска состоит из нескольких шагов:
- Инициализация начальных значений весовых коэффициентов и выбор значения скорости обучения (learning rate).
- Прямое распространение (forward propagation) - подача входных данных на вход сети и получение предсказанных значений.
- Вычисление значения функции ошибки (функции потерь) между предсказанными и истинными значениями.
- Обратное распространение (backpropagation) - вычисление градиента функции ошибки по весовым коэффициентам сети.
- Обновление весовых коэффициентов сети согласно градиенту и выбранному значению скорости обучения.
- Повторение шагов 2-5 до достижения заданной точности или определенного количества итераций.
Градиентный спуск позволяет нейронной сети автоматически настраивать свои весовые коэффициенты таким образом, чтобы минимизировать функцию ошибки. Суть работы алгоритма заключается в итеративном обновлении весовых коэффициентов в направлении, противоположном градиентному вектору функции ошибки. Таким образом, алгоритм "спускается" вниз по градиенту функции ошибки и находит локальный минимум либо стационарную точку.
Градиентный спуск может быть применен для обучения различных типов нейронных сетей, включая многослойные перцептроны (MLP), сверточные нейронные сети (CNN), рекуррентные нейронные сети (RNN) и другие. Однако, при выборе значения скорости обучения важно учитывать компромисс между скоростью сходимости и возможностью застрять в локальных минимумах функции ошибки.
| Преимущества | Недостатки |
|---|---|
| Простота реализации и понимания | Может застрять в локальных минимумах |
| Алгоритм работает даже для больших нейронных сетей | Чувствителен к выбору скорости обучения |
| Позволяет обучать нейронные сети с большим количеством весов | Может требовать много времени на обучение |
Градиентный спуск в нейронных сетях
Градиентный спуск основан на используемой в математическом анализе и оптимизации идее поиска локального минимума функции путем движения в сторону наиболее крутого убывания функции. В нейронных сетях градиентный спуск применяется для обновления весовых коэффициентов сети, итеративно рассчитывая градиент функции потерь по весам и обновляя их в направлении наиболее быстрого убывания функции потерь.
Процесс градиентного спуска в нейронных сетях включает в себя несколько этапов. В начале происходит прямой проход, в ходе которого данные пропускаются через сеть, и для каждого примера из обучающего набора вычисляется значение функции потерь. Затем происходит обратное распространение ошибки, в ходе которого градиент функции потерь по весам рассчитывается с использованием правила цепочки. После этого происходит обновление весов методом градиентного спуска с заданным шагом обучения.
| Этапы градиентного спуска в нейронных сетях |
|---|
| 1. Прямой проход |
| 2. Обратное распространение ошибки |
| 3. Обновление весов методом градиентного спуска с заданным шагом обучения |
Основное преимущество градиентного спуска в нейронных сетях заключается в его способности находить локальные оптимумы функции потерь. Однако, при использовании градиентного спуска могут возникать проблемы, такие как затухание или взрыв градиента, что может затруднить сходимость модели к глобальному оптимуму функции потерь. Для решения данных проблем применяются различные методы оптимизации, такие как стохастический градиентный спуск, адаптивный градиентный спуск и другие.
Роль градиентного спуска в обучении нейронных сетей

Градиентный спуск основан на идее последовательного обновления параметров сети в направлении, противоположном градиенту функции потерь. Градиент функции показывает направление наискорейшего возрастания функции. Используя обратное его направление, градиентный спуск сводит задачу оптимизации к поиску минимума функции потерь.
Градиентный спуск начинает с случайных значений параметров и итеративно обновляет их, используя градиент функции потерь. В каждой итерации значения параметров корректируются на основе скорости обучения, которая определяет шаг, с которым происходит изменение параметров. Большой шаг может привести к расходимости, а слишком маленький - к медленной сходимости. Поэтому выбор оптимального значения скорости обучения является важным аспектом в обучении нейронных сетей.
Градиентный спуск может быть реализован в нескольких вариантах, включая стохастический, мини-пакетный и пакетный градиентный спуск. Стохастический градиентный спуск использует только один случайно выбранный образец из обучающего набора для вычисления градиента. Мини-пакетный градиентный спуск использует небольшой поднабор из обучающего набора, а пакетный градиентный спуск использует все образцы. Каждый вариант имеет свои преимущества и недостатки и выбор зависит от требуемой эффективности и вычислительных ограничений.
Роль градиентного спуска в обучении нейронных сетей не может быть переоценена. Он позволяет модели находить оптимальные значения параметров в пространстве большой размерности. Это делает нейронные сети мощным инструментом в задачах классификации, регрессии и обработки данных.
Проблемы градиентного спуска в нейронных сетях

Однако, градиентный спуск может столкнуться с несколькими проблемами:
1. Проблема исчезающего градиента: При обратном распространении ошибки градиентами сети, градиенты могут снижаться экспоненциально с каждым новым слоем, что приводит к исчезающему градиенту. Это затрудняет обновление весов в начальных слоях сети и может приводить к низкой скорости обучения.
2. Проблема взрывающегося градиента: В отличие от исчезающего градиента, взрывающийся градиент возникает, когда градиенты становятся очень большими. Это может приводить к нестабильности и затруднять сходимость алгоритма обучения.
3. Локальные минимумы: Градиентный спуск имеет тенденцию сходиться к локальным минимумам функции потерь, а не к глобальному минимуму. В случае сложных функций потерь или большого числа параметров сети, это может стать проблемой и привести к недообучению.
4. Плато: На некоторых участках функции потерь градиент может быть нулевым или очень близким к нулю. Это приводит к затуханию обновления весов, и алгоритм может застрять в регионе с низкой ошибкой без достижения глобального минимума.
5. Скорость обучения: Выбор правильной скорости обучения является сложной задачей. Слишком большая скорость может привести к расходимости, а слишком маленькая - к медленной сходимости или застреванию в плато.
Решение данных проблем требует тщательного настройки гиперпараметров алгоритма обучения, а также использования методов оптимизации, таких как адаптивный градиентный спуск или стохастический градиентный спуск с мини-батчами.
Методы оптимизации градиентного спуска

1. Стохастический градиентный спуск (SGD)
Стохастический градиентный спуск является наиболее простым вариантом градиентного спуска. В этом методе градиент вычисляется только на одном случайном подмножестве обучающих примеров, что позволяет более быстро обновлять параметры модели и избегать локальных минимумов. Однако, SGD обычно имеет большую дисперсию и могут возникать проблемы с сходимостью.
2. Мини-пакетный градиентный спуск (Mini-batch GD)
Мини-пакетный градиентный спуск является промежуточным вариантом между SGD и полным градиентным спуском. В этом методе градиент вычисляется на случайном подмножестве обучающих примеров, но размер этого подмножества (мини-пакета) задается пользователем. Мини-пакетный градиентный спуск обычно имеет более стабильную сходимость и меньшую дисперсию, чем SGD.
3. Методы с адаптивным шагом обучения
Методы с адаптивным шагом обучения, такие как Adam, Adagrad, RMSprop, учитывают историю градиентов, чтобы адаптировать шаг обучения к различным параметрам модели. Это позволяет более эффективно и быстро сходиться к оптимуму и избегать проблем с выбором подходящего шага обучения.
4. Регуляризация
Регуляризация является дополнительной техникой, которая позволяет уменьшить переобучение и улучшить обобщающую способность модели. Две наиболее распространенные техники регуляризации - L1 регуляризация (стандарт Lasso) и L2 регуляризация (стандарт Ridge). Регуляризация добавляет штраф к функции потерь на основе нормы вектора параметров модели, что позволяет сделать параметры модели менее комплексными и более устойчивыми к шумам в данных.
Таким образом, выбор подходящего метода оптимизации градиентного спуска в нейронных сетях является важным шагом в обучении модели. Каждый метод имеет свои преимущества и недостатки, и их выбор зависит от конкретной задачи и доступных ресурсов.
Применение градиентного спуска в реальных задачах

Градиентный спуск, являющийся основным алгоритмом обновления параметров нейронных сетей, широко применяется в различных реальных задачах. Ниже представлены несколько примеров использования градиентного спуска в практике:
| Задача | Применение градиентного спуска |
|---|---|
| Обработка изображений | В задачах компьютерного зрения градиентный спуск используется для обучения нейронных сетей на больших наборах изображений. Он позволяет оптимизировать параметры модели, улучшая ее способность распознавать и классифицировать объекты на изображениях. |
| Обработка естественного языка | В задачах анализа текста и обработки естественного языка, градиентный спуск используется для настройки весовых коэффициентов в рекуррентных нейронных сетях. Это позволяет создавать модели, способные генерировать текст, анализировать его смысл и выполнять другие задачи, связанные с обработкой языка. |
| Рекомендательные системы | В задачах построения рекомендательных систем, градиентный спуск используется для обучения моделей, которые предлагают пользователям персонализированные рекомендации на основе их предпочтений и истории. Он позволяет оптимизировать параметры модели, улучшая ее точность и релевантность рекомендаций. |
Это лишь несколько примеров применения градиентного спуска в реальных задачах. Однако, его использование может быть найдено практически во всех областях, где применяются нейронные сети и машинное обучение.



