Функции являются важным понятием в математике и экономике. Они описывают зависимость между различными переменными и помогают в анализе и оптимизации различных процессов. Одним из важных свойств функций является их выпуклость.
Выпуклость функции означает, что график функции выгнут вверх или вниз. Если функция выпукла вверх, то график функции будет выгибаться вверх и иметь форму "волны". Если функция выпукла вниз, то график функции будет выгибаться вниз и иметь форму похожую на букву "U".
Выпуклость функции является важным понятием в экономике, так как она позволяет определить направление изменения функции при изменении переменных. Если функция выпукла вниз, то увеличение одной переменной приведет к уменьшению значения функции, а увеличение другой переменной приведет к увеличению значения функции. Если функция выпукла вверх, то будет наблюдаться обратная зависимость.
Функция выпукла вверх или вниз: что это означает?
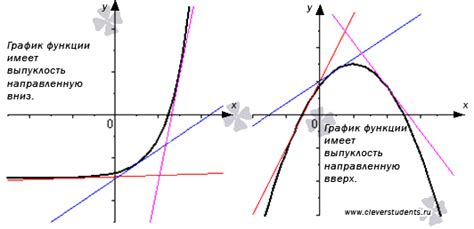
При изучении функций, мы часто сталкиваемся с понятиями выпуклости вверх или вниз. Однако, что же они значат и как это влияет на форму графика?
Когда говорят, что функция выпукла вверх, это означает, что ее график вогнут вверх. То есть, если бы мы были находились внутри функции и смотрели на окружающие нас точки графика, мы бы видели, что они образуют вогнутую вверх кривую.
Функция, которая выпукла вниз, имеет график, который выглядит выпуклым вниз, то есть, образует вогнутую вниз кривую. Если бы мы находились внутри функции, мы бы видели, что точки графика образуют вогнутую вниз форму.
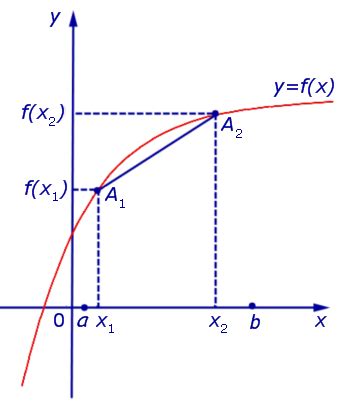
Кривизна функции может быть полезна для анализа и определения ее свойств. Например, у выпуклой вверх функции есть свойство, что любой отрезок между двумя точками графика всегда лежит выше самого графика. То есть, если мы возьмем две точки на графике, отрезок, соединяющий их, всегда будет лежать выше самого графика. Аналогично, для функции, которая выпукла вниз, отрезок будет лежать ниже самого графика.
Теперь, когда мы понимаем, что значит функция выпукла вверх или вниз, мы можем использовать эту информацию для анализа и понимания функций, их свойств и графиков.
Определение функции выпукла вверх или вниз
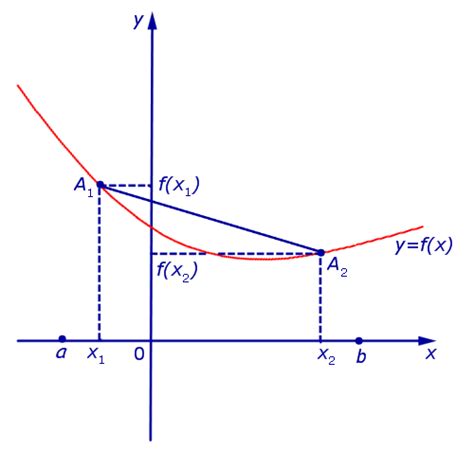
Функция является выпуклой вверх, если ее график при движении по нему образует вогнутость вниз. Это означает, что любая прямая, соединяющая две точки на графике функции, лежит выше самого графика.
Существует также понятие строгой выпуклости и строгой вогнутости. Функция строго выпуклая вниз, если ее график при движении по нему образует строгую вогнутость вверх, и не существует ни одной прямой, соединяющей две точки на графике функции, которая бы лежала ниже самого графика. Аналогично, функция строго выпуклая вверх, если ее график при движении по нему образует строгую вогнутость вниз, и не существует ни одной прямой, соединяющей две точки на графике функции, которая бы лежала выше самого графика.
Отличительной особенностью функции, являющейся выпуклой вверх или вниз, является то, что у нее есть точка перегиба - точка, в которой изменяется кривизна графика, и график функции меняет направление вогнутости. Эта точка на графике функции является местом перехода между выпуклостью и вогнутостью.
Критерии для функции, выпуклой вверх
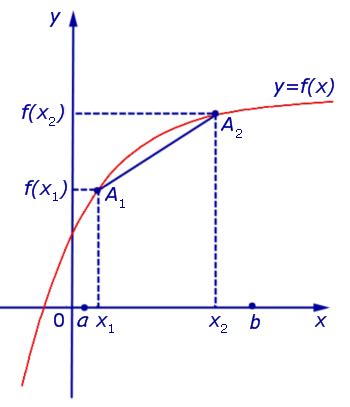
1. Выпуклость вверх: Вначале следует понять, что означает сам термин "выпуклость вверх". Функция называется выпуклой вверх, если все ее точки лежат ниже графика касательной в каждой точке.
2. Знак производной: Вторая производная функции должна быть положительной на заданном интервале. Если вторая производная функции положительна на всем интервале, то функция является выпуклой вверх на этом интервале.
3. Точки перегиба: В функции, выпуклой вверх, существуют точки перегиба, где производная меняет знак. В таких точках функция переходит из выпуклой вогнутой. То есть, на интервалах между точками перегиба функция выпуклая вверх, а вне этих интервалов - вогнутая.
4. Графическое представление: Для определения выпуклости функции вверх можно построить ее график и провести касательные в разных точках. Если все касательные находятся выше функции и не пересекают ее, то функция является выпуклой вверх.
Таким образом, критерии для функции, выпуклой вверх, включают положительность второй производной, наличие точек перегиба и графическое представление.
Критерии для функции, выпуклой вниз
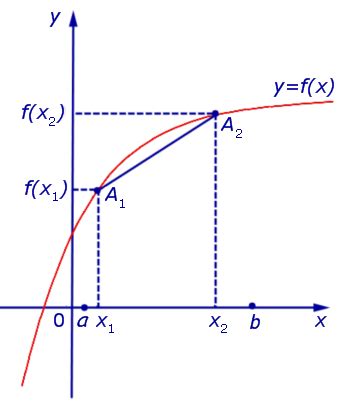
Функция называется выпуклой вниз (вогнутой вверх), если для любых двух точек, лежащих на графике функции, отрезок, соединяющий эти точки, лежит всецело под графиком.
Таким образом, если для любых точек A и B, где A(x1, y1) и B(x2, y2), выполнено неравенство:
y > ((y2 - y1) / (x2 - x1)) * (x - x1) + y1
где (x, y) - произвольная точка на графике функции, то функция является выпуклой вниз.
Другими словами, график функции выпуклой вниз имеет форму "впадины".
Основные критерии функции, выпуклой вниз:
- Все точки на графике, лежащие между двумя точками А и В, также должны находиться ниже отрезка, соединяющего эти точки.
- Коэффициент наклона прямой, определяющей отрезок АВ, должен быть убывающим (знак минус) на всем интервале между А и В.
- Вторая производная функции должна быть положительной на всей области определения функции.
Пример функции выпуклой вверх
Рассмотрим пример функции f(x) = x^2 - 2x + 1. Построим таблицу значений функции:
| x | f(x) |
|---|---|
| 0 | 1 |
| 1 | 0 |
| 2 | 1 |
| 3 | 4 |
| 4 | 9 |
Построим график функции:
На графике видно, что для любых двух точек графика функции отрезок, соединяющий эти точки, лежит выше графика функции. Таким образом, функция f(x) = x^2 - 2x + 1 является функцией выпуклой вверх.
Пример функции выпуклой вниз
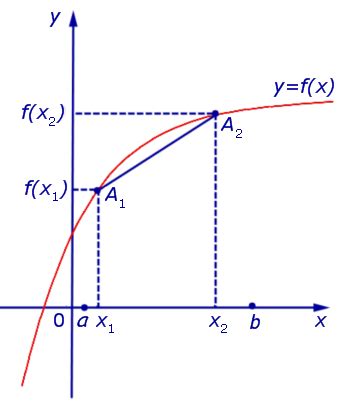
Рассмотрим пример функции, которая является выпуклой вниз.
Пример:
Функция: f(x) = x^2
Графиком данной функции является парабола, которая открывается вниз. Как видно из графика, для любых двух точек на функции отрезок, соединяющий эти точки, будет лежать ниже графика функции.
Таким образом, функция f(x) = x^2 является примером функции, которая выпукла вниз.
Свойства функций, выпуклых вверх
Функция называется выпуклой вверх, если ее график лежит поверх всех своих касательных на заданном интервале. Другими словами, любой участок кривой, соединяющий две точки на графике, лежит выше отрезка, проведенного между этими точками.
У функций, выпуклых вверх, существует несколько важных свойств:
- Точка пересечения с касательной: каждая касательная графика функции, выпуклой вверх, пересекает график в единственной точке. Это свойство позволяет однозначно определить точку пересечения и найти ее координаты.
- Монотонное возрастание: функция, выпуклая вверх, может иметь только монотонно возрастающие участки на заданном интервале. Вся кривая будет стремиться "выпукнуться" вверх.
- Определенность второй производной: чтобы функция была выпуклой вверх, ее вторая производная должна быть положительной на всем интервале. Вторая производная показывает, как меняется наклон функции в каждой ее точке. Если вторая производная положительна, это означает, что функция имеет "выпуклую" форму.
Функции, выпуклые вверх, широко применяются в различных областях, таких как оптимизация, экономика, финансы и другие. Их свойства и характеристики позволяют анализировать поведение функций и принимать важные решения на основе полученных данных.
Свойства функций, выпуклых вниз
Функция, выпуклая вниз, представляет собой функцию, график которой образует чашеобразную кривую, открытую вниз. В контексте математики, такая функция имеет следующие свойства:
- Любой отрезок, соединяющий две точки на графике функции, лежит ниже самой функции.
- Вторая производная функции всегда положительна или равна нулю на всей области определения.
- Локальные минимумы функции находятся во внутренних точках, а глобальный минимум – в точке с наименьшим значением функции.
- Линии уровня функции, то есть линии, которые соединяют точки с одинаковым значением функции, имеют форму линий, сходящихся к точке минимума.
- На графике функции можно выделить касательные прямые, все они будут лежать ниже графика.
Использование функций, выпуклых вниз, часто встречается в экономике и оптимизации задач. Например, при решении задачи оптимального распределения ресурсов или при анализе функции полезности потребителя.
Применение функций, выпуклых вверх или вниз

Функции, выпуклые вверх или вниз, имеют широкое применение в различных областях, включая экономику, математику, физику и оптимизацию. Эти функции имеют важные свойства и используются для решения различных задач.
Функции, выпуклые вверх
- Инвестиции: Для принятия решения об инвестициях в компанию или проект требуется моделирование стоимости акций. Функции, выпуклые вверх, могут быть использованы для определения оптимального времени для покупки или продажи акций.
- Оптимизация: Многие задачи оптимизации требуют максимизации или минимизации функции. Функции, выпуклые вверх, используются в таких задачах для определения оптимального значения переменных.
- Математическое моделирование: Функции, выпуклые вверх, могут быть использованы для моделирования различных явлений, таких как рост популяции, спрос на товары и т.д.
Функции, выпуклые вниз
- Физика: Функции, выпуклые вниз, используются для описания веществ и материалов, которые могут быть сжаты или согнуты при воздействии внешних сил.
- Экономика: Многие экономические модели требуют моделирования функций с отрицательной выпуклостью, чтобы учитывать эффекты экстра-экономического поведения.
- Оптимизация распределения ресурсов: Функции, выпуклые вниз, используются для определения эффективного распределения ограниченных ресурсов с учетом различных факторов.
Таким образом, функции, выпуклые вверх или вниз, представляют собой важный инструмент для моделирования и анализа различных явлений и задач. Их применение позволяет получить оптимальные решения и более глубокое понимание рассматриваемых процессов.
1. Функция, выпуклая вверх, имеет "положительный" вид. Наклон касательной к графику функции в каждой его точке строго возрастает, а значит, функция увеличивается быстрее от своей касательной. График такой функции может быть представлен в виде "вогнутого" параболического кривого.
2. Функция, выпуклая вниз, имеет "отрицательный" вид. Наклон касательной к графику функции в каждой его точке строго убывает, а значит, функция увеличивается медленнее от своей касательной. График такой функции может быть представлен в виде "выпуклого" параболического кривого.
3. Функции выпуклости вверх и вниз имеют важное применение в оптимизации и экономике. Важно уметь распознавать и анализировать такие функции, так как выпуклость может указывать на наличие минимумов или максимумов функции, а также помогать в решении задач экономического планирования и оптимизации.
Итак, функция выпуклая вверх, функция выпуклая вниз - это важные понятия, которые помогают нам лучше понять и анализировать характер функций и их графиков.




