Коэффициент b - это одно из ключевых понятий в математическом анализе и статистике. Он играет важную роль в линейной регрессии и графически представляет величину сдвига графика функции по вертикальной оси.
Значение коэффициента b позволяет проанализировать, насколько сильно зависимая переменная изменяется при изменении независимой переменной. Если коэффициент b положительный, то увеличение значения независимой переменной приводит к увеличению зависимой переменной. Если же коэффициент b отрицательный, то увеличение значения независимой переменной приводит к уменьшению зависимой переменной.
Значение коэффициента b можно интерпретировать как сдвиг графика функции вдоль оси OY. Если b положительный, то график функции будет по-прежнему отклонен вверх, а если b отрицательный, то график будет отклоняться вниз. Чем больше по модулю значение коэффициента b, тем сильнее сдвиг графика.
Коэффициент b в графике: значение и зависимость
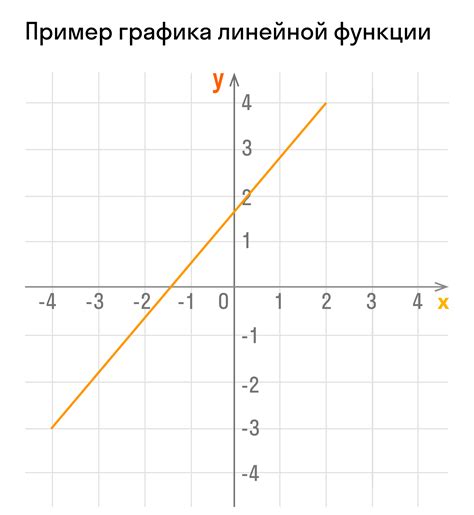
Значение коэффициента b указывает на точку пересечения графика с осью ординат (ось y). Если коэффициент b положителен, то график будет пересекать ось y в положительной области. Если он отрицателен, то график будет пересекать ось y в отрицательной области. Если же b равно нулю, то график будет проходить через начало координат.
Зависимость значений коэффициента b от других переменных в уравнении функции может быть различной в разных случаях. Например, если коэффициент b зависит от коэффициента m, изменение m приведет к изменению наклона графика, но сам коэффициент b останется неизменным.
В таблице ниже приведены некоторые примеры значений коэффициента b:
| Значение коэффициента b | Наклон графика | Точка пересечения с осью ординат |
|---|---|---|
| b > 0 | Восходящий | Выше начала координат |
| b = 0 | Горизонтальный | Через начало координат |
| b | Нисходящий | Ниже начала координат |
Изучение значения и зависимости коэффициента b в графиках помогает в понимании и анализе математических функций, а также в решении различных задач и приложений в физике, экономике и других науках.
Определение и значение коэффициента b

В графике функции, коэффициент b отвечает за сдвиг графика в вертикальном направлении. Он определяет значение y-координаты точки пересечения графика с осью ординат.
Коэффициент b можно найти, рассмотрев уравнение функции вида y = mx + b, где m - коэффициент наклона (угловой коэффициент) и b - коэффициент сдвига. Значение коэффициента b представляет собой точку пересечения графика с осью ординат при x = 0.
Зная значение коэффициента b, можно определить вертикальное положение графика на плоскости. Если b положительное число, то график функции будет сдвинут вверх, относительно оси ординат. Если b отрицательное число, то график функции будет сдвинут вниз, относительно оси ординат.
Важно отметить, что значение коэффициента b играет ключевую роль в определении положения и формы графика функции. Изменение его значения может значительно изменить положение графика относительно оси ординат.
Коэффициент b в зависимости от других переменных
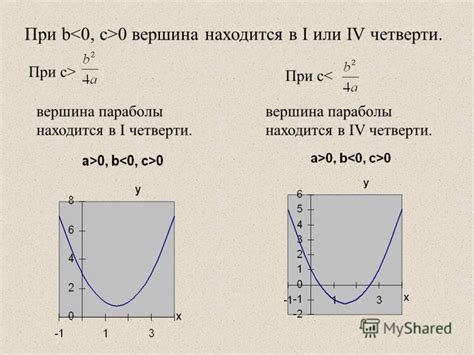
Значение коэффициента b позволяет определить, насколько изменится зависимая переменная при изменении независимой переменной на одну единицу. Если коэффициент b положительный, то с увеличением независимой переменной зависимая переменная также будет возрастать. В случае отрицательного значения коэффициента b, при увеличении независимой переменной зависимая переменная будет убывать.
Значение коэффициента b может быть интерпретировано как скорость изменения зависимой переменной относительно независимой переменной. Чем больше абсолютное значение коэффициента b, тем сильнее связь между переменными.
Для определения значения коэффициента b в зависимости от других переменных, используется метод наименьших квадратов. Этот метод позволяет найти наилучшую прямую, приближающую зависимость между переменными. Математический расчёт коэффициента b основывается на анализе отклонений значений переменных от найденной прямой.
Интерпретация значения коэффициента b

В уравнении зависимости y от x вида y = ax + b, коэффициент b представляет собой значения, на которое график функции сдвигается по оси y.
Значение коэффициента b может иметь следующую интерпретацию:
- Положительное значение b указывает на то, что график функции смещен вверх по оси y. Чем больше значение b, тем больше смещение.
- Отрицательное значение b указывает на то, что график функции смещен вниз по оси y. Чем меньше значение b, тем больше смещение.
- Коэффициент b может равняться нулю, что означает, что график функции не смещен по оси y.
Точное определение значения коэффициента b зависит от контекста задачи и конкретной функции, которую мы рассматриваем. Однако, с учетом указанных интерпретаций, мы можем использовать значение коэффициента b для определения вертикального смещения графика функции.
Значение и использование коэффициента b в реальной жизни

В экономике коэффициент b может использоваться для анализа зависимости между различными переменными. Например, он может помочь оценить влияние изменения цены на товары на спрос или предложение. Если коэффициент b положительный, то это может означать, что с увеличением цены спрос на товар уменьшается, а снижение цены приводит к его увеличению. Если коэффициент b отрицательный, то это может указывать на прямую зависимость - увеличение цены ведет к увеличению спроса, а снижение цены - к его уменьшению.
В физике коэффициент b может использоваться для описания различных явлений. Например, в уравнении движения свободного падения коэффициент b отражает силу сопротивления воздуха. Чем больше значение этого коэффициента, тем сильнее будет сопротивление воздушной среды, и тем медленнее будет падение тела. Это позволяет более точно описывать и предсказывать движение объектов в атмосфере.
Коэффициент b также может быть использован в других областях, таких как биология, социология, геология и т.д. Например, в биологии его значение может отражать зависимость между различными характеристиками организма, такими как размер, вес или скорость роста. В социологии коэффициент b может отражать влияние различных факторов на поведение людей или динамику общества.
| Область | Пример использования |
|---|---|
| Экономика | Анализ зависимости между ценой и спросом на товары |
| Физика | Описание движения объектов в атмосфере |
| Биология | Зависимость между размером организма и его весом |
| Социология | Влияние различных факторов на поведение людей |



