Формула S ab sin a является одной из основных формул в геометрии и тригонометрии. Она используется для вычисления площади треугольника, если известны длины двух его сторон a и b, а также величина угла между этими сторонами a.
Формула может быть представлена следующим образом: S = ab sin a, где S - площадь треугольника, a и b - длины сторон треугольника, a - величина угла между сторонами a и b.
Эта формула основана на принципе, что площадь треугольника можно выразить с помощью полупроизведения длин двух его сторон и синуса угла между ними. Синус угла a показывает, насколько сильно стороны треугольника отклонены от параллельных линий.
Формула S ab sin a находит применение в различных областях, включая астрономию, физику, строительство и географию. Она позволяет определить площадь треугольника, зная только длины его сторон и величину угла между ними. Это удобно, например, при выполнении геодезических измерений или расчете площадей территорий на картах.
Формула синуса: что это и как применяется
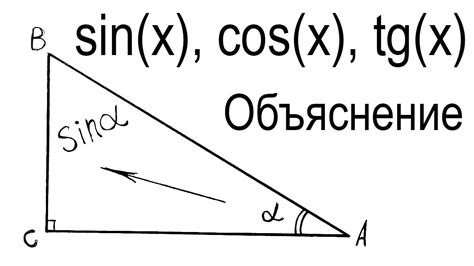
Сама формула выглядит следующим образом:
sin(a) = AB / AC
Где:
- sin(a) - значение синуса угла a
- AB - длина противолежащего катета
- AC - длина гипотенузы
Формула синуса находит применение в геометрии и тригонометрии. Она является одной из основных тригонометрических формул и используется для решения различных задач, связанных с прямоугольными треугольниками. Например, с помощью формулы синуса можно найти длину недостающей стороны треугольника или вычислить значение угла, если известны длины сторон.
Формула синуса основывается на свойстве синуса угла в прямоугольном треугольнике: он равен отношению длины противолежащего катета к длине гипотенузы.
Зная значения сторон треугольника и используя формулу синуса, можно решать различные задачи в геометрии, навигации и физике. Например, формула синуса используется для расчетов высоты объектов, определения расстояний и нахождения углов наклона.
Расчеты и применение формулы синуса
Формула синуса угла в прямоугольном треугольнике имеет вид:
| sin(a) = a / c |
Где:
- a - длина противоположного катета;
- c - длина гипотенузы.
Формула позволяет вычислить значение синуса угла по известным длинам сторон треугольника. Синус используется в геометрии, физике, астрономии и других науках для решения различных задач.
Пример использования формулы синуса:
- Пусть в прямоугольном треугольнике известны значения катета a = 3 и гипотенузы c = 5.
- Вычисляем значение синуса угла a по формуле: sin(a) = 3 / 5 = 0.6.
Таким образом, синус угла a в данном треугольнике равен 0.6.
Формула синуса является одной из основных формул тригонометрии и широко применяется в различных областях знаний.
Примеры использования формулы синуса

1. Нахождение длины стороны треугольника
Если известны угол α и длина стороны b, можно найти длину стороны a с помощью формулы:
a = b / sin(α)
Например, для треугольника, где α = 30° и b = 5 см, длина стороны a будет:
a = 5 / sin(30°) ≈ 10 см
2. Решение треугольников
Синусы углов используются при решении задач с треугольниками. Например, для задачи нахождения угла β, если известны длины сторон a и c, можно использовать формулу:
sin(β) = a / c
Таким образом, зная длины сторон a = 6 см и c = 8 см, можно рассчитать значение угла β:
sin(β) = 6 / 8 ≈ 0.75
β ≈ 48.59°
3. Определение высоты треугольника
Если известны длины основания b и угла α, можно найти высоту треугольника h с помощью формулы:
h = b * sin(α)
Например, для треугольника, где α = 60° и b = 10 см, высота будет:
h = 10 * sin(60°) ≈ 8.66 см
Формула синуса является важным инструментом в геометрии и тригонометрии и широко применяется для решения различных задач.
Доказательство формулы синуса

После этого проведем высоту треугольника, и несмотря на то, что доказательство может быть сложно представить словами, оно однако основано на геометрической интерпретации синуса.
Заметим, что между стороной a и осью OX угол равен a. Проведем линию из начала координат до точки, лежащей на стороне b и перпендикулярной направлению оси OX. Тогда получится прямоугольный треугольник с катетами a и b, где гипотенуза является прямоугольной линией. Таким образом, справедлива формула:
S = ab * sin(a).
Именно поэтому формулу S=ab*sin(a) можно использовать для вычисления площади треугольника, зная длины двух его сторон и меру угла между ними.



