Доли – это особый вид дробей, с которым знакомятся ученики в 6 классе. Вообще, доли можно встретить не только в уроках математики, но и в повседневной жизни. Знание основных понятий и правил работы с долями очень важно, так как они помогут ученикам лучше понять дроби, которые являются основой многих учебных программ.
Доля представляет собой дробное число, обозначающее часть от целого. Например, если мы разделим пирог на 8 равных частей и возьмем одну из них, то это будет означать, что мы взяли 1/8 от пирога. В данном случае, число 1 называется числителем, а число 8 – знаменателем. Числитель показывает, сколько частей мы взяли, а знаменатель указывает на общее количество частей, на которые разделен целый объект.
В 6 классе, ученики начинают изучать основные операции с долями. Важно уметь складывать, вычитать, умножать и делить доли, а также сравнивать их между собой. Для выполнения этих операций используются простые правила, с которыми несложно разобраться. Знание основных понятий и навыков работы с долями поможет ученикам успешно справиться с более сложными задачами в будущем.
Определение долей

Доли состоят из двух чисел: числителя, который показывает, сколько частей от общего количества имеется, и знаменателя, который показывает, на сколько частей разделено целое.
Например, если в корзине 8 яблок, а 3 из них зеленые, то доля зеленых яблок – это 3/8. В этом случае числитель равен 3 (количество зеленых яблок), а знаменатель равен 8 (общее количество яблок в корзине).
Доли могут быть эквивалентными, если их значения одинаковы. Например, доли 2/4 и 1/2 являются эквивалентными, потому что они обе показывают половину от общего количества.
Запись долей

Числитель - это количество частей, которые мы имеем. Например, в дроби 3/4 число 3 - это количество частей, которые у нас есть.
Знаменатель - это количество частей, на которые делится целое. В случае дроби 3/4 число 4 - это количество равных частей, на которые мы делим целое.
Для записи доли используется специальный формат: числитель/знаменатель. Например, дробь 3/4 означает, что у нас есть 3 части из 4 возможных.
Знак деления между числителем и знаменателем может быть представлен различными символами, такими как косая черта (/) или двоеточие (:). Однако в учебниках и математических заданиях чаще всего используется косая черта (/).
Например:
- 1/2 - одна половина
- 2/3 - две трети
- 3/4 - три четверти
Запись долей используется для различных задач, таких как укладывание плитки на пол или распределение конфет между детьми. Знание записи долей поможет вам легче решать такие задачи и понимать доли в математике.
Сравнение долей

При работе с долями в математике возникает необходимость сравнения различных долей, чтобы определить, какая из них больше или меньше.
Для сравнения долей необходимо использовать общий знаменатель. Если доли уже имеют общий знаменатель, просто сравниваются их числители. Большее значение числителя означает большую долю, а меньшее значение числителя - меньшую долю.
Если у долей разные знаменатели, их необходимо привести к общему знаменателю. Для этого можно воспользоваться наименьшим общим кратным (НОК) знаменателей долей.
После приведения долей к общему знаменателю их можно сравнивать. Большее значение числителя по-прежнему будет означать большую долю, а меньшее значение числителя - меньшую долю.
Важно помнить, что при сравнении долей необходимо учитывать их целевую величину. Например, если сравниваются доли в процентах, то можно использовать преобразование в десятичную или дробную форму для удобства сравнения.
Приведение долей к общему знаменателю
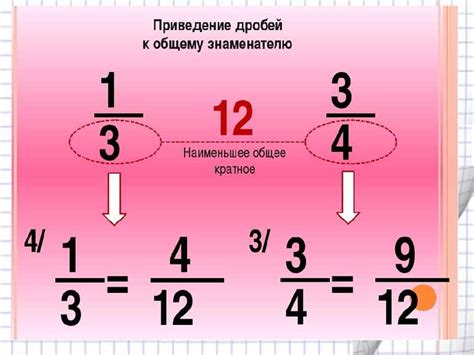
Для приведения долей к общему знаменателю необходимо выполнить следующие шаги:
- Найти наименьшее общее кратное (НОК) знаменателей данных долей.
- Умножить каждую дробь на такие дополнительные множители, чтобы знаменатель каждой доли стал равным НОК.
- После приведения всех долей к общему знаменателю можно складывать или сравнивать дроби.
Например, рассмотрим две доли: 1/2 и 3/4. Чтобы привести их к общему знаменателю, найдем НОК знаменателей 2 и 4, который равен 4. Затем умножим первую дробь на 2/2 и получим 2/4, а вторую дробь умножим на 1/1 и она останется 3/4. Теперь обе дроби имеют общий знаменатель 4 и их можно сравнивать или складывать.
Приведение долей к общему знаменателю также позволяет упростить доли. Например, если после приведения общий знаменатель равен 6, то доли 2/6 и 3/6 можно записать как 1/3 и 1/2 соответственно. Это делается путем сокращения долей при группировке долей с одинаковым общим знаменателем.
Операции с долями

Сложение долей выполняется только в том случае, если знаменатели долей одинаковы. Если знаменатели равны, то сложение проводится только с числителями, а знаменатель остается без изменений.
Вычитание долей также производится только в том случае, если знаменатели равны. При вычитании числитель одной доли вычитается из числителя другой, а знаменатель остается таким же.
Умножение долей выполняется путем умножения числителей и знаменателей долей. Полученные значения числителя и знаменателя могут быть сокращены, если они имеют общие делители.
Деление долей производится путем умножения первой доли на обратную второй долю. Обратная доля получается путем перестановки местами числителя и знаменателя.
Работа с долями помогает ученикам развить навыки работы с дробями и понять, как применять их в реальных ситуациях, например, при расчетах с деньгами или при дележе предметов на равные части.
Примеры задач с долями

Доли широко используются в математике и повседневной жизни. Рассмотрим несколько примеров задач, в которых нужно работать с долями:
- Задача 1: Столяр замерил длину доски и выразил ее в виде дроби: 4/5 м. Затем он отпилил от доски 1/4 м. Какова стала длина доски после пиления?
- Задача 2: В пироге было 6 равных кусочков. Ребята съели 3/4 пирога. Сколько кусочков пирога осталось?
- Задача 3: В торте было 8 равных частей. Мальчик съел 3/8 торта, а девочка съела 1/4 торта. Кто съел больше торта?
Решение: Изначальная длина доски равна 4/5 м. Если отпилить 1/4 м, то останется 1 - 1/4 = 3/4 длины. Таким образом, длина доски после пиления составит 3/4 м.
Решение: Изначально в пироге было 6 кусочков. Если ребята съели 3/4 пирога, то останется 6 - 6 * 3/4 = 6 - 18/4 = 6 - 9/2 = 6 - 4.5 = 1.5 кусочка пирога.
Решение: Если мальчик съел 3/8 торта и девочка съела 1/4 торта, то можно выразить их потребление в общих долях: мальчик съел 3/8 + девочка съела 1/4 = 6/16 + 4/16 = 10/16. Так как 10/16 > 1/2, то можно сказать, что в итоге девочка съела больше торта.
Таким образом, задачи с долями возникают в различных ситуациях, и знание работы с долями позволяет решать такие задачи и понимать их смысл.



