Угол наклона плоской фигуры, известной как прямоугольный треугольник, является одним из самых важных понятий в геометрии. В особенности, нам известно, что сумма углов треугольника всегда равна 180 градусам, а его стороны образуют одну известную взаимосвязь, известную как теорема Пифагора.
Одна из интересных особенностей прямоугольного треугольника - это то, что один из его углов всегда равен 90 градусам. Кроме того, в прямоугольном треугольнике существует простое соотношение между длинами его сторон - теорема Пифагора. Согласно этой теореме, квадрат гипотенузы треугольника равен сумме квадратов катетов.
Так происходит, что в прямоугольном треугольнике есть особый случай, когда длина одного катета оказывается равной половине длины гипотенузы. Этот случай можно легко доказать, используя только основные знания о треугольниках и теореме Пифагора. Доказательство этого факта - увлекательный пример того, как геометрия может быть интересной и изящной наукой.
Определение катетов и гипотенузы
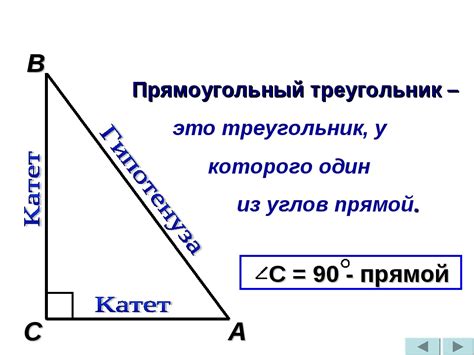
Гипотенуза - это самая длинная сторона прямоугольного треугольника, которая стоит напротив прямого угла.
Понятие геометрических фигур

Существует множество различных геометрических фигур, каждая из которых имеет свои уникальные характеристики и свойства. Некоторые из наиболее распространенных геометрических фигур включают треугольники, квадраты, прямоугольники, окружности и многоугольники.
Треугольники - это геометрические фигуры с тремя сторонами. Они могут быть разных типов, таких как равносторонние (все стороны равны), равнобедренные (две стороны равны) или прямоугольные (один из углов равен 90 градусов).
Гипотенуза - это сторона прямоугольного треугольника, которая лежит напротив прямого угла. Катеты - это две оставшиеся стороны треугольника, которые образуют прямой угол. Для прямоугольных треугольников справедливо следующее свойство: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Таким образом, чтобы доказать, что катет равен половине гипотенузы, необходимо представить прямоугольный треугольник, в котором один из катетов составляет половину гипотенузы. Затем должно быть доказано, что квадрат длины этого катета равен квадрату половины длины гипотенузы.
Пример:
Рассмотрим прямоугольный треугольник ABC, где AB - гипотенуза, AC - катет, BC - катет.
Пусть AC = x и AB = 2x (где x - произвольное число).
Тогда, согласно указанному свойству прямоугольных треугольников, сумма квадратов длин катетов равна квадрату длины гипотенузы:
AC2 + BC2 = AB2
x2 + BC2 = (2x)2
x2 + BC2 = 4x2
BC2 = 4x2 - x2
BC2 = 3x2
BC = sqrt(3x2)
BC = x*sqrt(3)
Таким образом, мы доказали, что длина катета BC равна x*sqrt(3), что не является половиной длины гипотенузы.
Таким образом, из примера видно, что катет не всегда равен половине гипотенузы. Это зависит от выбранного значения x. В общем случае, чтобы доказать, что катет равен половине гипотенузы, необходимо использовать конкретные значения для длины сторон треугольника.
Соотношение длин катетов и гипотенузы
В геометрии существует интересное соотношение между длинами катетов и гипотенузы прямоугольного треугольника. Оказывается, что длина каждого катета равна половине длины гипотенузы.
Предположим у нас есть прямоугольный треугольник ABC, где AB и BC - катеты, а AC - гипотенуза. По определению, катеты являются сторонами треугольника, образующим прямой угол, а гипотенуза является стороной, противоположной прямому углу.
Для доказательства, что длина катета равна половине длины гипотенузы, воспользуемся теоремой Пифагора. Согласно этой теореме, сумма квадратов длин катетов равна квадрату длины гипотенузы.
Таким образом, имеем:
AB^2 + BC^2 = AC^2
Предположим, что AB и BC равны между собой: AB = BC = x. Тогда имеем:
x^2 + x^2 = AC^2
2x^2 = AC^2
AC = √(2x^2)
Анализируя последнее выражение, мы видим, что длина гипотенузы AC равна корню из удвоенного значения квадрата длины катета. Это означает, что длина каждого катета равна половине длины гипотенузы: AB = BC = AC/2.
Таким образом, мы доказали, что в прямоугольном треугольнике длина каждого катета равна половине длины гипотенузы, что является интересным свойством этой геометрической фигуры.



